结合阈值法和模极大值法的冲击加速度信号降噪
卿 涛,丁问司
(华南理工大学 机械与汽车工程学院,广东 广州 510640)
0 引言
交变冲击机构的冲击性能考核主要是测定冲击能和冲击频率,因此得到冲击机构在整个工作周期中的运动参数变化(冲击活塞的速度曲线和位移曲线)是测定冲击性能指标的关键。国内外常用应力波法、触点法、非接触式光电位移微分法、高速摄影法、示功图法和气压法等[1]对交变冲击机构的冲击性能进行测试,但是上述的测试方法都是间接对冲击机构的速度和位移进行测定。目前对于速度和位移的测量已经出现了很多新方法和相关精密仪器,然而在实际的应用过程中,还是存在各种各样的问题。
小波变换广泛应用于非平稳信号的处理领域,具有低熵性、多分辨分析、去相关性等特点[2]。目前,小波降噪方法主要有空域相关降噪法、模极大值降噪法和阈值降噪法。其中小波模极大值方法的难点是如何确定一个合适的搜索区间,并且采用交替投影算法重构小波系数具有执行效率慢、不稳定等问题。小波阈值方法在信噪比较低的场合去噪效果不明显,而且会保留非信号传播路径上的高频噪声。文献[3]分别使用小波模极大值方法和小波阈值法对液压冲击器的冲击加速度信号进行降噪,这两种方法只处理了其中的高频噪声,没有将分形噪声引起的低频漂移现象考虑进去。在利用微机电加速度计对交变冲击机构的测试过程中,所获取的信号常常包含加速度计本身传感轴的偏移误差、自身的电路噪声以及外界的干扰噪声。而其中含有的分形噪声会引起交变冲击加速度信号慢漂移,可归属为低频噪声[4]。
考虑到后续移动端APP去噪算法编码的难易和已有算法存在的问题,本文利用阈值降噪法来改善模极大值法降噪过程中模极大值点搜索效率低的问题,并利用分段埃尔米特插值重构算法[5]重构小波系数来降低算法的时间复杂度和提高算法的鲁棒性。
1 小波模极大值去噪原理
若有一个函数f(x)在x0附近满足式(1)[6],则称α为函数f(x)在x0处的李氏指数,即:
|f(x0+h)-pn(x0-h)|≤t|h|α.
(1)
其中:pn(x0-h)为一个过f(x0+h)的n次多项式;h为充分小量;t为常数。
李氏指数α表示函数在某一点处的奇异性, 并且α越大函数在该点处的奇异性越小;α越小函数在该点处的光滑度越差。
设小波函数为Ψ(x)并且连续可微,如果在x0点的任意邻域内对函数f(x)任意尺度内的小波变换存在k>0常数,使得对所有x0点邻域内的小波变换满足不等式(2),则函数f(x)在点x0处有一致的李氏指数:
|Wsf(x)|≤ksα.
(2)
其中:s为尺度;Ws为小波变换。
对式(2)两边同时取对数,化简得到信号f(x)的李氏指数与小波变换的模极大值关系:
log2|Wsf(x)|≤log2k+αlog2s.
(3)
当进行二进离散小波变换时,s=2j(j为小波变换尺度),则式(3)变为:
log2|W2jf(x)|≤log2k+jα.
(4)
在式(4)中,小波变换尺度j与李氏指数α以乘积jα的形式出现,从而可以得出小波变换模极大值随尺度j或李氏指数α变化的规律。对于常用信号,当α>0时,分解尺度的增大会使模极大值也变大;α<0时,分解尺度的减小会使模极大值也变小。对于噪声而言,其所对应的α一般小于0,因此信号和噪声在小波变换的各尺度上存在截然相反的传播特性,从而达到对信号降噪的目的。
2 阈值降噪方法
小波阈值去噪方法的关键是如何选取阈值规则以及阈值量化函数。目前阈值的选取有以下4种方案[7]:固定阈值、Stein无偏似然估计阈值、混合型阈值和最大最小阈值。从所研究的信号出发,选择合适的阈值方案和阈值函数对小波系数做门限阈值处理。硬阈值函数和软阈值函数分别为:

(5)

(6)
其中:y为处理后的小波系数;x为小波分解系数;λ为阈值。
与硬阈值函数相比,软阈值函数会对信号进行压缩,存在恒定偏差,因此软阈值函数降噪会丢失奇异点,并且对信噪比较低的信号降噪效果不明显。根据实测的加速度信号可知,信号的奇异性较大,为了更好地保留信号中的奇异性,本文选用硬阈值函数对小波系数做门限阈值处理。
借鉴文献[8],本文采用改进的变阈值策略:首先确定最大尺度J上的门限阈值为T0=C·M/J(C根据信号的实际情况进行赋值,M为当前尺度上全部模极大值中的最大值),保留大于等于最大尺度上阈值的模极大值,将小于最大尺度上阈值的模极大值置零。在1~(J-1)分解尺度上将门限阈值设置为T0=C·M2/ln(j+1),采用硬阈值函数量化小波系数。
3 重构信号的降噪方法
根据采用硬阈值函数以及自适应阈值规则改进小波模极大值点搜索的思路,本文提出的降噪方法具体实现步骤如下:
(1) 对实测含噪信号序列{f(ni),i>0}做多尺度二进小波变换,求出不同尺度上的小波系数序列。

(3) 在尺度j=J-1上寻找尺度J上模极大值点
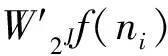
(4) 重复步骤(3),直到尺度j=2为止。
(5) 在最小尺度上保留相邻高尺度上模极大值点位置处大于阈值的极值点,从而得到最小尺度上的模极大值点。

图1 本文提出的小波降噪算法流程
4 仿真实验与工程应用
4.1 仿真实验
选用MATLAB中具有冲击特征的Bumps信号进行仿真实验。信号的采样点数为1 024个,采样时间为1 s。向原始Bumps信号中添加分形噪声[10]、白噪声和脉冲噪声,因此输入信号可以用以下的方程来表示:
f(n)=s(m)+h(m)+w(m).
(7)
其中:s(m)为原始信号;h(m)为分形噪声;w(m)为高斯白噪声。
本文选用db6小波,分解层数为3层,采用前文所述的阈值选取规则,依次使用普通模极大值降噪法、文献[11]中提出的基于SURE自适应阈值的模极大值降噪方法和本文方法对如图2(a)所示的含噪Bumps信号进行降噪处理,所得的效果如图2(b)~图2(d)所示。

图2 多种方法对含噪Bumps信号的降噪结果
由图2(b)可以看出,普通模极大值降噪法在t=0.53 s附近出现尖峰,在t=0.68 s和t=0.97 s附近出现信号重叠;由图2(c)可以看出,文献[11]降噪方法在第5个突变点处的信号没有其他算法那么光滑;由图2(d)可知,本文降噪法具有更好的光滑性,较好地保留了信号中的奇异性。
通过比较均方根误差(RMSE)和信噪比(SNR)的大小可以直观地判断算法的降噪效果,均方根误差和信噪比的计算公式如下:
(8)
(9)

计算得到的三种降噪算法的均方根误差和信噪比见表1。

表1 三种降噪算法的均方根误差和信噪比比较
根据表1可以得出本文方法的均方根误差明显要低于其他两种方法,并且信噪比也要优于其他两种方法,证明本文降噪法的去噪性能有所提升。
各降噪法执行环境一致,用执行时间来表征算法的执行效率,将各算法分别执行10次,取平均值作为最终执行时间。不同含噪信号三种降噪算法从开始处理信号到运行结束的执行时间见表2。将文献[11]降噪法与普通降噪法的执行时间相比较,可知阈值规则以及量化函数的选取可以提高搜索效率,从而减少执行时间;将本文降噪法与文献[11]方法的执行时间相比较,可知使用分段埃尔米特插值重构算法比使用交替投影重构算法的执行效率快。

表2 不同含噪信号三种降噪算法执行时间比较
4.2 工程应用
本文选择交变液压冲击器作为被测对象,采用微机电系统(MEMS)加速度传感器作为测量元件搭建测试系统。某次实验采集到的实测冲击加速度信号如图3(a)所示,在所选小波基函数和分解层数相同的情况下,分别使用本文降噪法、普通降噪法和文献[11]降噪法对信号进行降噪处理,降噪效果如图3(b)~图3(d)所示。比较图3(b)~图3(d)可知,本文降噪法较好地保存了冲击信号的能量,与其他两种降噪法相比冲击特征也更为明显,并且本文降噪法相比其他两种方法具有更好的降噪性能,提高了执行效率。

图3 不同降噪法的去噪效果
5 结论
本文根据小波硬阈值降噪法、小波模极大值降噪法和分段埃尔米特插值重构算法各自具有的优点,将它们结合起来,得到了一种结合阈值法和模极大值法的新去噪方法。在仿真实验和工程应用中,与其他降噪算法的降噪效果进行了对比分析。结果表明,本文方法降噪效果更好,执行效率更高,计算更加稳定,有利于提高后续速度积分和位移积分的精度,并且算法时间复杂度的降低和鲁棒性的提升为移动端APP实现数据在线处理和分析奠定了基础,有利于实现冲击机构控制的智能化。

