基于RL电路的球状地质体瞬变电磁观测电位改正*

韩 阳，李文尧，马 松，隆季原

(昆明理工大学 国土资源工程学院,云南 昆明 650093)

0 引言

时间域瞬变电磁法 (TEM)是一种建立在电磁感应原理基础上的人工源电磁探测方法[1]。瞬变电磁法可应用于找矿采矿[2-3]、工程物探[4-6]、地质调查[7-9]等领域，是一种应用广泛的物探方法。近十几年来，时间域电磁法技术得到了很大的发展[10-11]，取得了良好的应用效果。

瞬变电磁法接收线圈可以等效为线圈内阻、电感和匹配电阻组成的RL电路。在该电路中，地质体的感应电位等于接收线圈内阻电位、接收线圈电感电位、接收线圈匹配电阻电位(观测电位)之和。目前大多数TEM方法使用接收线圈的观测电位近似代替地质体的感应电位，这会产生误差，导致反演和推断解释结果不可靠。蒋邦远[12]对局部地质体的观测电位进行了理论研究。王华军[13]研究了层状地质体用观测电位代替地质体感应电位产生的误差。因此，需要找到一种由观测电位改正到地质体感应电位的方法。本文结合前人研究[14-17]，基于基尔霍夫定律和球状地质体中心回线瞬变电磁法观测电位表达式，提出了一种球状地质体瞬变电磁接收线圈观测电位改正方法。

1 球状地质体接收线圈观测电位公式

接收线圈的等效RL电路如图1所示。

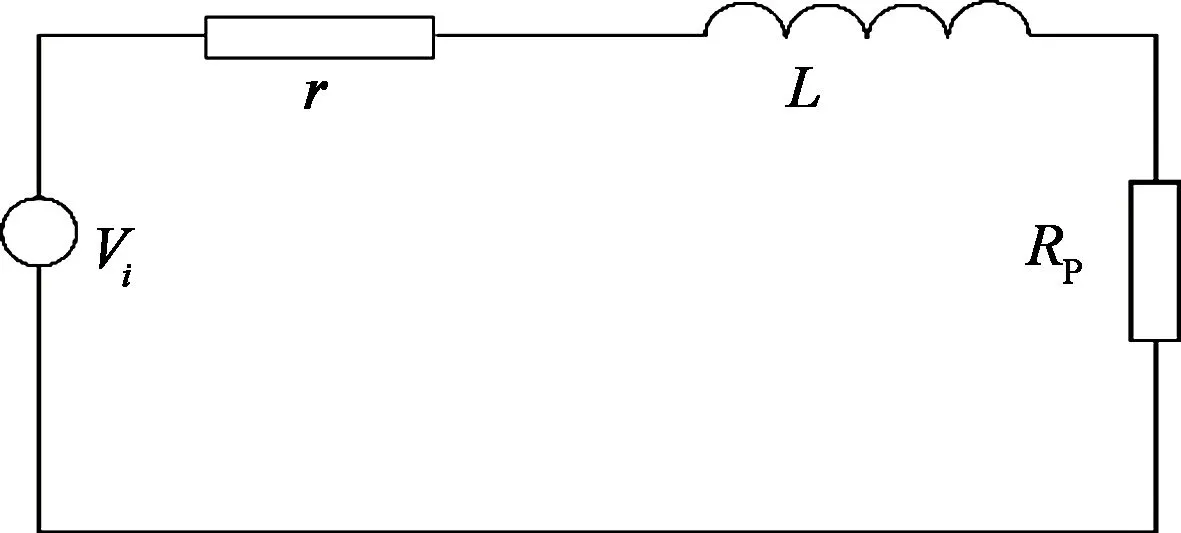
图1 瞬变电磁接收线圈等效RL电路

根据基尔霍夫电压定律有

Vi=Vr+VL+VRP，

(1)

式中：VL为来源于线圈的感应电位；Vr为线圈的电阻产生的电位，r为线圈内阻；RP为匹配电阻；L为接收线圈电感。

(2)

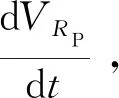
地质体感应电位与地质体形状有关，不同形状的地质体有不同的观测电位的理论公式，本文针对球状地质体，推导其观测电位的理论公式。

假设电导率为σ、半径为a、中心埋深为h的球体位于圆形发射回线的正下方，中心回线装置下瞬变电磁场的表达式[1]为

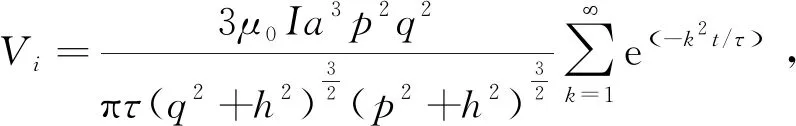
(3)

式中：q为接收线圈半径；p为圆形发射回线的发射半径；I为发射电流；τ为扩散系数 ，τ=μ0σa2/π2，μ0=4π×10-7H/m。

在晚期条件下，根据文献[1]中得到的t≈τ/2时进入晚期，可将式(3)简化为

(4)

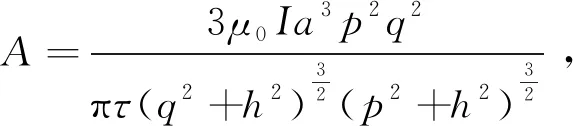
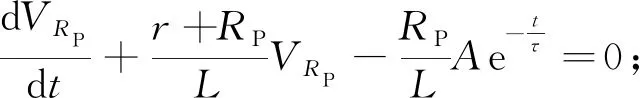
(5)

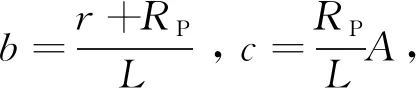
(6)

求解以上公式得到方程的解：

(7)

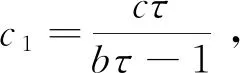
(8)

(9)

式(9)即为球状地质体观测电位公式。

2 球状地质体瞬变电磁观测电位改正方法

式(9)中的RP、r、L为仪器参数，是已知的，而τ和A是未知的，因此不能直接使用式(9)计算VRP。通过野外观测可得VRP，曲线形态为指数形式，故可用野外观测数据进行曲线拟合得到VRP表达式。

曲线拟合的原理是根据采集到的大量实验数据(xi，yi)(i=1,2,…,n)求出y=f(x)一个近似表达式y=φ(x)(称为“拟合函数”)。从几何角度看，就是要根据采集到的n个点(xi，yi)，求曲线y=f(x)的一条近似曲线y=φ(x)，与之能较好地逼近[18]。常采用最小二乘法逼近,表达式为

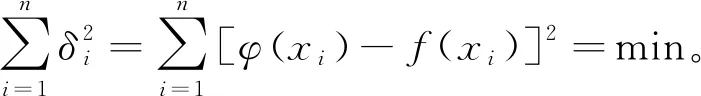
(10)

选取φ(x)使偏差的平方和最小。

令VRP(t)=meit+nejt，其中j为已知参数，m、n、i为未知参数。

已知观测时间与对应时间的观测电位{(ti,VRPi),i=0,1,2,…,m}，采用曲线拟合的方法得到m=m1,n=n1,i=i1时达到最好的拟合效果，拟合表达式为

VRP=m1ei1t+n1ejt。

(11)

将拟合得到的VRP求导得

(12)

将式(12)代入式(2)得

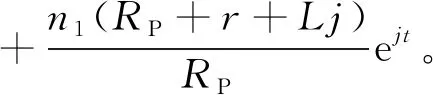
(13)

式(13)即为改正后的观测电位公式，其中m1、n1、i1为拟合得到的参数。将观测时间t代入式(13)，即可得到各个时间改正后的观测电位。

3 改正方法有效性及稳定性分析

野外观测电位数据是离散的，且有误差，为了验证该方法的有效性，需进行改正方法有效性和稳定性分析。本文提出的改正方法是基于晚期条件下简化公式推导的,步骤如下：

a.假设已知球状地质体半径a=50 m，电导率σ=1 S/m，埋深h=80 m，线圈电感L=0.02 H，匹配电阻RP=100 Ω，线圈内阻r=10 Ω, 供电电流为10 A，发射回线半径为56.7 m，接收回线半径为5.73 m，t≈τ/2≈159 μs时进入晚期，可以用式 (4)计算地质体在159 μs之后的理论感应电压Vi。

b.根据式(9)计算出观测电位VRP的理论值，然后分别加入5%、10%、15%随机误差，对加入随机误差的VRP进行指数拟合，得到关于时间t的观测电位VRP的表达式。

c.对观测电位VRP表达式求一阶导数，并将VRP的拟合表达式及一阶导数表达式代入式(2)得到改正后的Vi值。

d.计算理论Vi和改正后Vi的相对误差，结果分别见表1、表2、表3。由表1-表3可知：加入5%的随机误差时，理论Vi值和改正后的Vi值之间的误差小于2.5%；加入10%的随机误差时，理论Vi值和改正后的Vi值之间的误差小于2%；加入15%的随机误差时，理论Vi值和改正后的Vi值之间的误差小于5%。加入随机误差(5%、10%、15%)时理论Vi值和改正后的Vi值之间的误差均小于5%。因此，该改正方法是有效且稳定的。

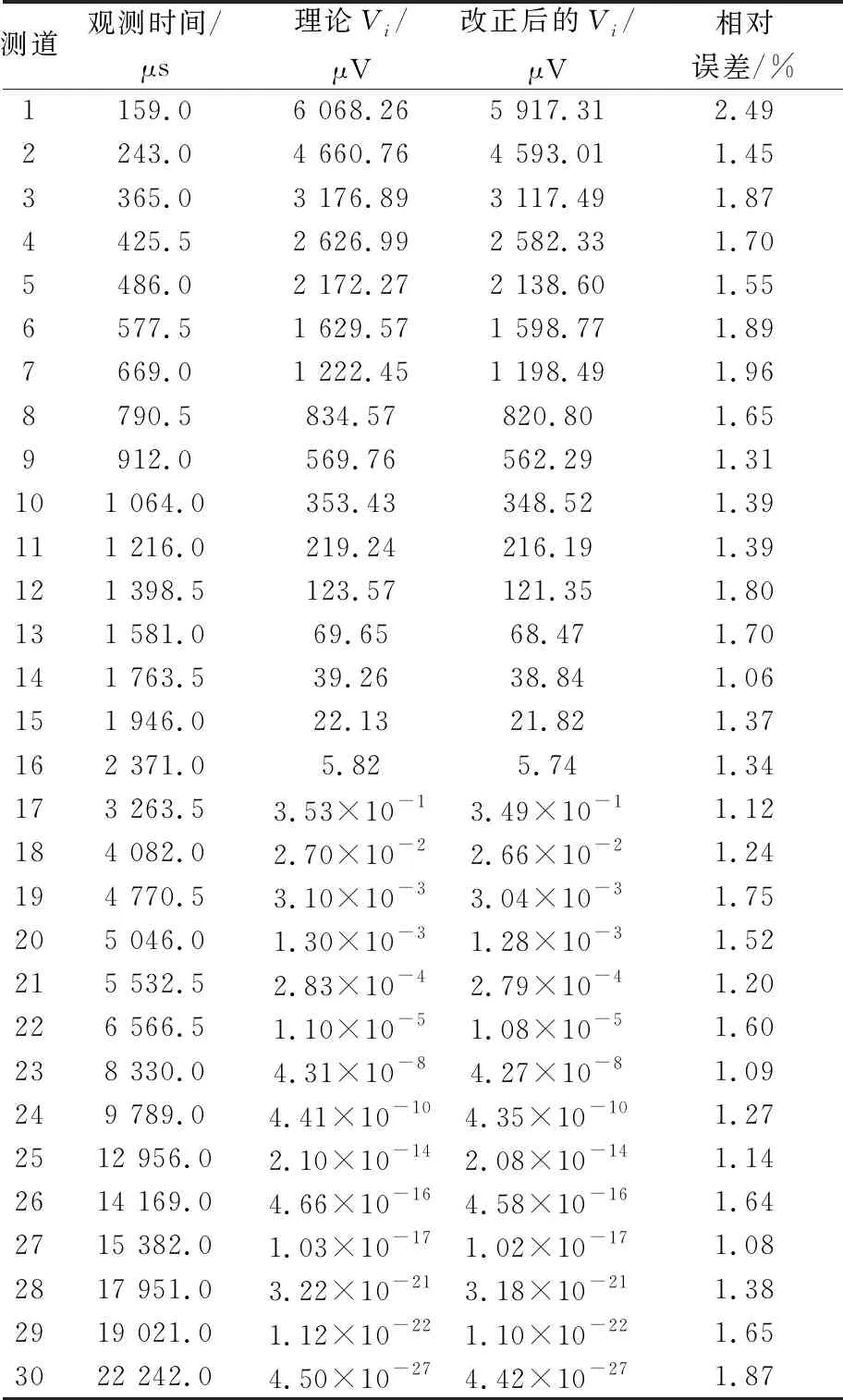
表1 理论Vi与改正后的Vi对比(加入5%随机误差)

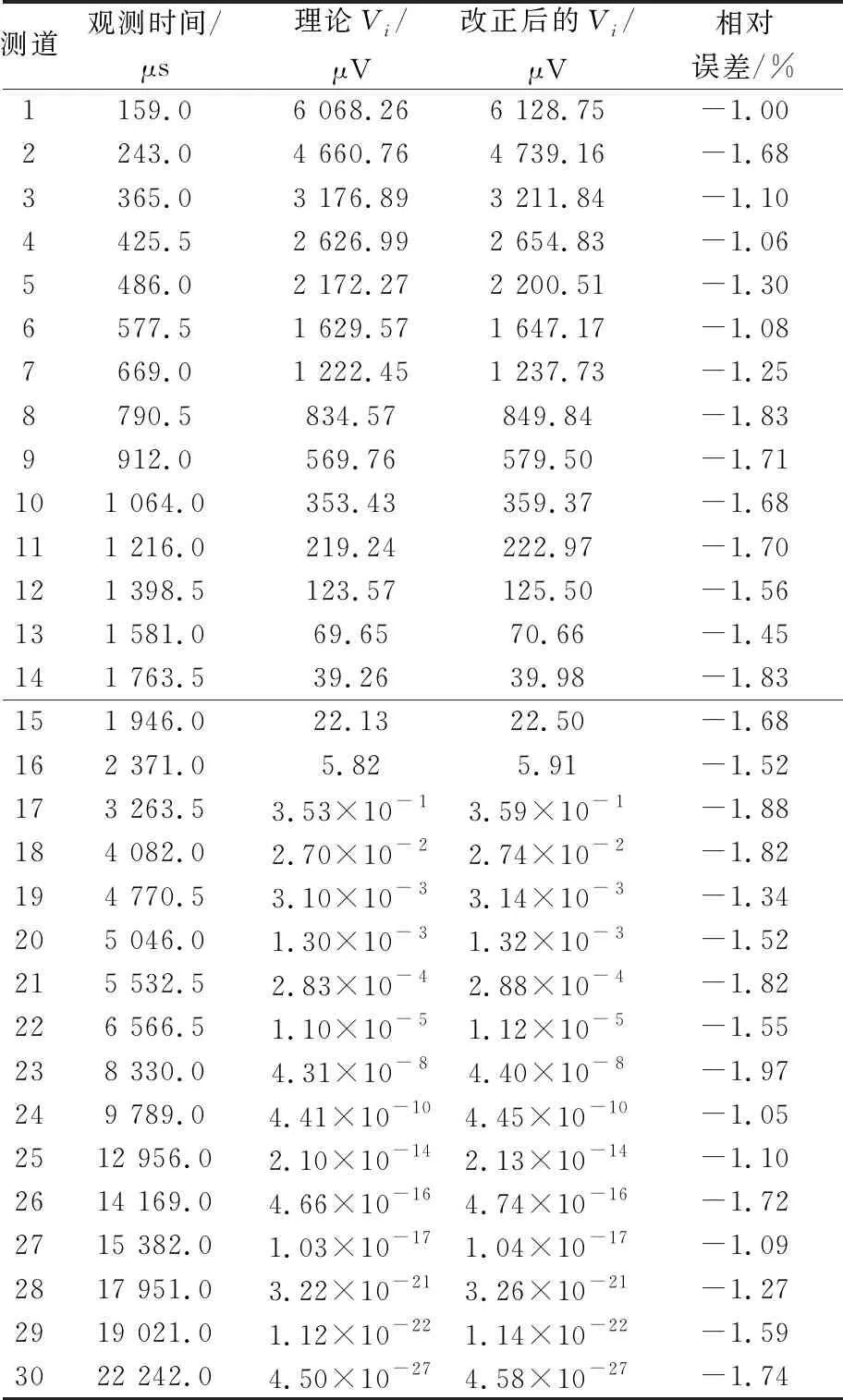
表2 理论Vi与改正后的Vi对比(加入10%随机误差)

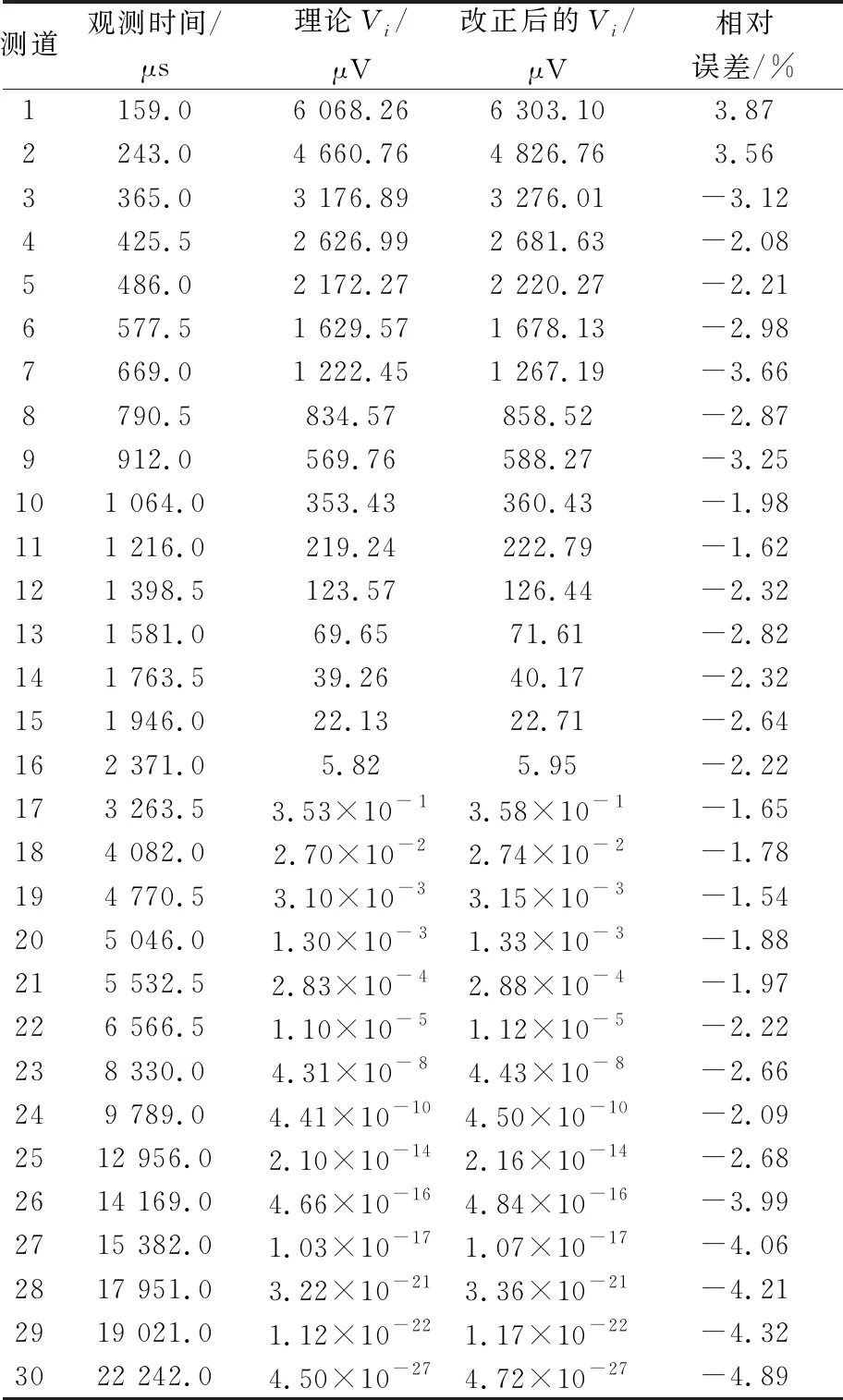
表3 理论Vi与改正后的Vi对比(加入15%随机误差)

4 用VRP代替Vi的误差分析

验证用VRP代替Vi产生的误差，步骤如下：

a.采用中心回线装置，发射回线半径56.7 m，接收回线半径5.73 m，供电电流10 A，匹配电阻RP=100 Ω，接收线圈内阻r=10 Ω，电感为L=0.02 H，获得观测电位VRP。

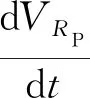
c.将观测时间t代入改正公式Vi的表达式算得改正后的电位Vi，并计算用VRP代替Vi的相对误差，结果见表4。

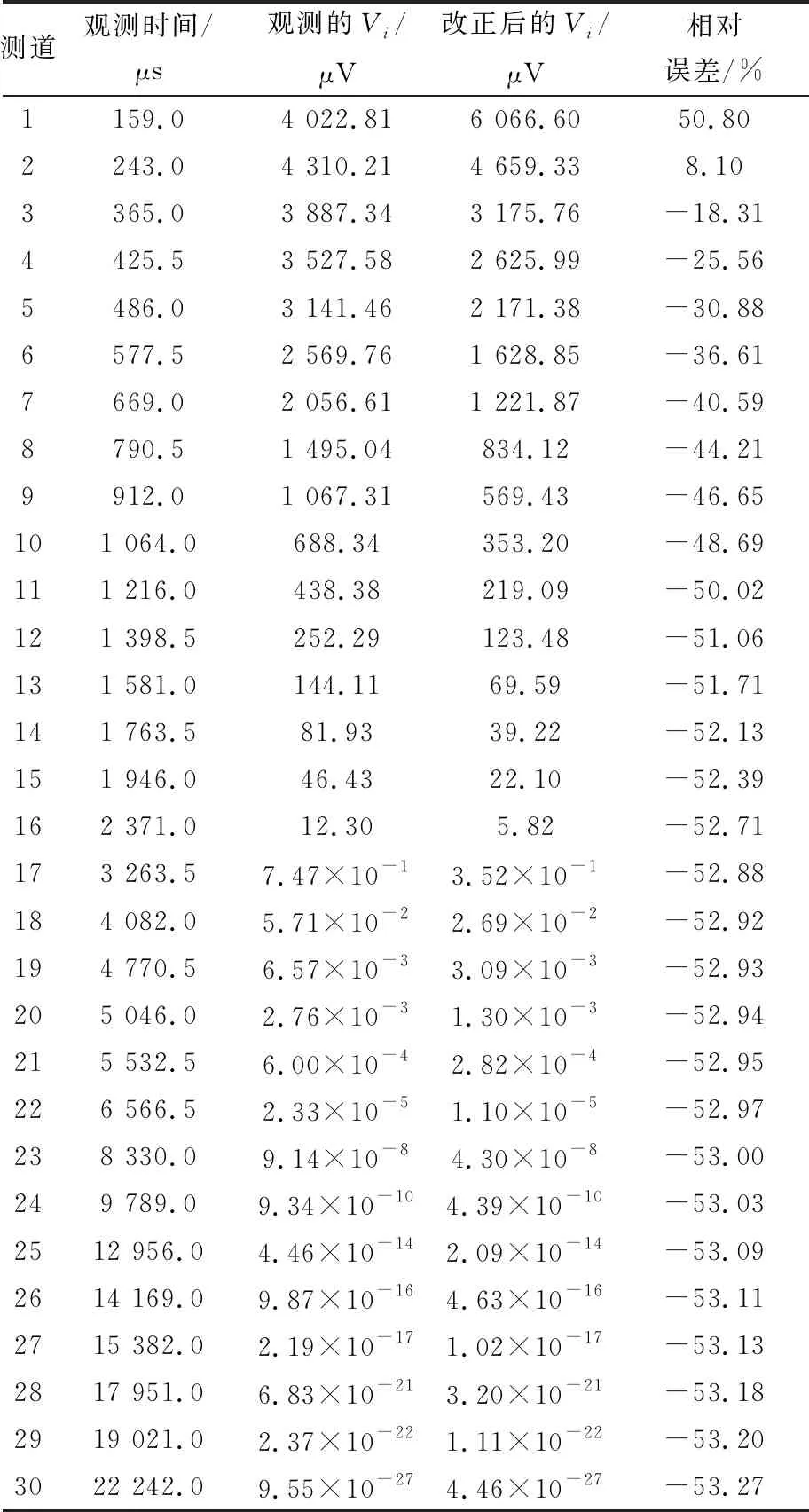
表4 用VRP代替Vi的相对误差

由表4可知：观测时间为159.0 μs时相对误差为50.80%；1 216.0 μs之后误差维持在50%左右；观测时间为22 242.0 μs时误差最大，为53.27%；243.0 μs误差最小，为8.10%。由此表明，在观测早期，观测电位VRP与地质体的感应电位Vi差别很大，用VRP代替Vi导致了探测结果的不可靠。

5 结论

目前大多数TEM系统是使用匹配电阻两端的电位作为观测电位近似代替地质体在接收线圈上的感应电压，这种方法在探测埋深较浅的地质体时会产生较大的数据误差，导致反演和推断解释结果不可靠。本文通过对瞬变电磁中心回线接收线圈等效电路的深入分析，将地质体的感应电位近似为接收线圈内阻电位、接收线圈电感电位、接收线圈匹配电阻电位(观测电位)之和。基于球状地质体中心回线瞬变电磁场表达式，通过公式推导，采用曲线拟合的方法，提出了球状地质体接收线圈观测电位改正方法。经验证，该方法有效且稳定，改正后的电位与理论电位误差小于5%。