机械活化对黄铁矿热自燃动力学特性的影响*

陈姿霖

(中钢集团武汉安全环保研究院有限公司，湖北 武汉 430080)

0 引言

煤自燃是目前煤矿安全生产面临的重大难题[1-2]，自燃引起的火灾一直威胁着矿山的安全生产，甚至造成人员伤亡。由于煤层中黄铁矿含量较高，黄铁矿易发生自燃[3]以及黄铁矿中的无机硫使煤更易氧化[4-5]，严重缩短了煤自燃发火期，因而易引发煤矿火灾。有研究表明,在开采过程中硫化矿石因受到不同形式的机械力作用而被活化，处于不稳定状态，易发生氧化自燃反应[6]，因此研究机械活化及未活化的黄铁矿的化学反应动力学机理尤为重要，可为研究黄铁矿对煤自燃的影响提供理论依据。

热分析是研究物质反应动力学的重要手段，应用广泛。阳富强等[7]采用Coats-Redfern积分法求出硫化矿石在不同升温速率下的活化能及指前因子，为硫化矿石自燃倾向性判定提供了依据；刘明强等[8]运用模式配合法和模式法对煤泥燃烧反应进行了动力学研究，推断出煤泥燃烧的最概然反应机理函数；陈娟等[9]采用Friedman法得到了不同粒径褐煤的动力学模型。然而不同的研究得到的动力学参数往往有很大差异，不仅与实验条件、仪器、试样有关，还与数据计算方法和反应机理的判别方法有关[10]。目前国际上推断机理函数的方法很多，其中Malek法是国际热分析和量热学协会公认的一种方法[11]。

张燕娟等[12]采用搅拌球磨对铁酸锌进行了机械活化，发现铁酸锌活化后与硫酸反应的表观活化能降低，化学反应活性提高；张有新等[13]研究发现，磁黄铁矿经振动磨机械活化后表观活化能降低，化学反应活性提高；张超等[14]研究了机械活化后黄铁矿的储能，也得到了机械活化后矿物的表观活化能会降低的结论，但尚未考虑机械作用后矿物粒径减小对表观活化能的影响[15]。因此，本文提出了最概然Malek法和Achar-Brindley-Sharp-Wendworth法分析体系，通过计算分析，推断出相近平均粒径下机械活化及未活化黄铁矿的机理函数以及动力学参数，并对得到的反应速率方程进行了验证，以期为预测及防止煤层中黄铁矿自燃提供理论依据。

1 实验

1.1 制样

黄铁矿试样取自安徽铜陵赫尔矿产品有限公司，采用Axios advanced X射线荧光光谱仪对试样的化学成分进行了分析，结果表明，该黄铁矿中ω(S)为 42.02%、ω(Fe)为 42.75%。

首先采用16目的标准筛筛分得到黄铁矿样品，再用200目标准筛筛分得到未活化的黄铁矿(样品1)，另用QM-BP型行星球磨机破碎黄铁矿样品5 min制备机械活化的黄铁矿(样品2)。

1.2 表征

采用Mastersizer 2000激光粒度仪测试样品1和样品2的平均粒径，得到样品的粒度累计分布(见图1)。由图1可知，样品1和样品2的平均粒径相差不大。

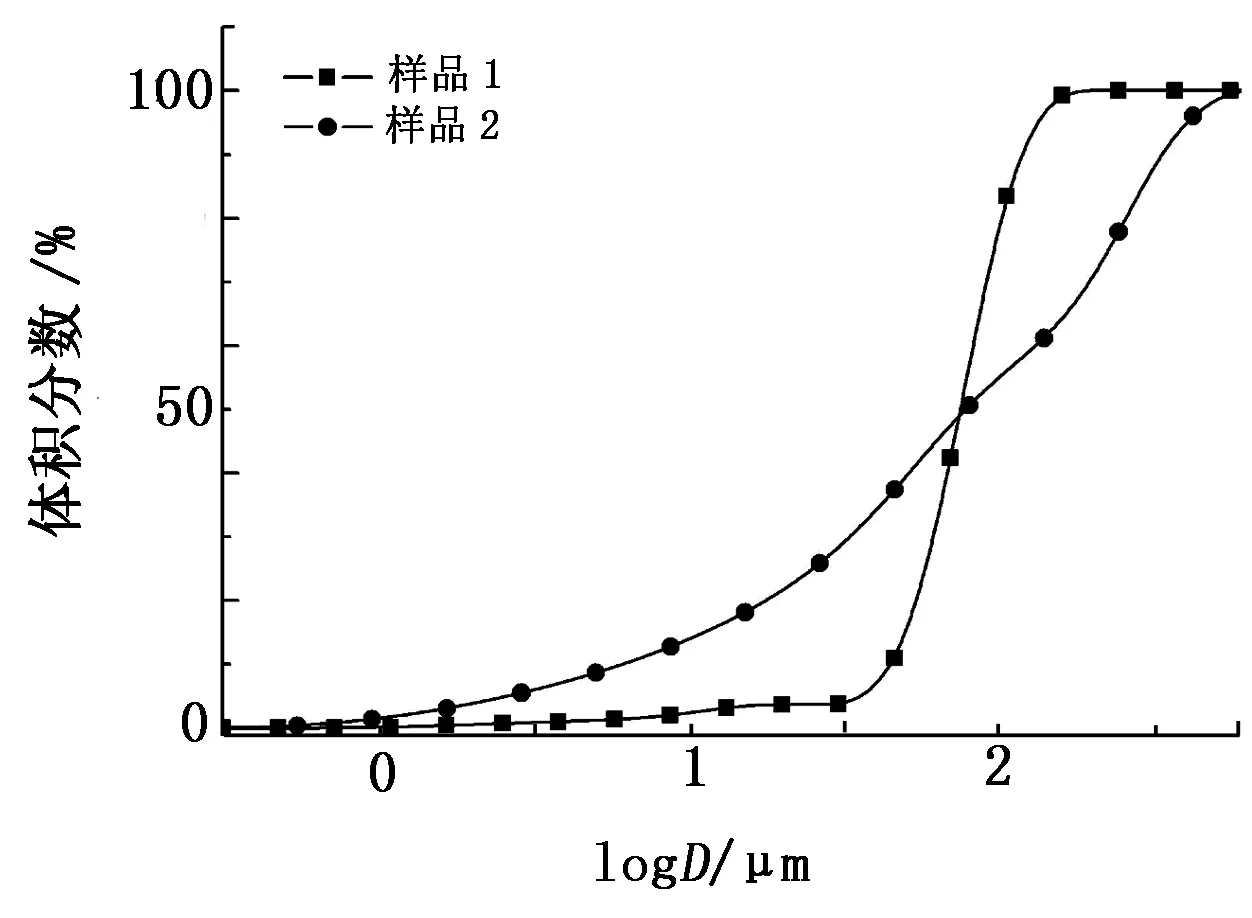
图1 样品的粒度累计分布(D为粒径)

采用X射线衍射仪(D8 Advance型)对样品的结构进行表征，分别得到样品1和样品2的X射线衍射(XRD)图谱(见图2)。使用MDI JADE5.0(XRD分析软件)对样品1和样品2 的XRD图谱的衍射峰进行分析拟合，得到样品的晶粒粒径和晶格畸变率(见表1)。由图2和表1可知，黄铁矿经机械活化后衍射峰强度宽化和增强，主要原因是机械活化导致黄铁矿结构改变，活化后的黄铁矿的晶粒粒径减小，晶格畸变率增大。

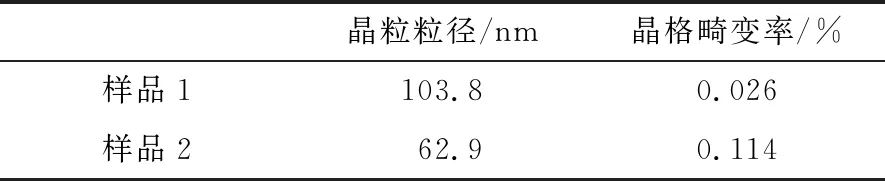
表1 黄铁矿样品的结构参数

图2 黄铁矿样品的XRD图谱

运用扫描电子显微镜(JSM-5610LV型)对样品1和样品2的形貌和微结构进行表征，得到对应的SEM图(见图3)。

由图3可知，机械活化后的黄铁矿粒度分布不均匀，矿物晶面存在缺陷、畸变，且部分细化后的矿粒附着在大块矿的表面。

1.3 实验方法

取10 mg样品1和样品2分别在升温速率为10、15、20 K/min，温度范围为50～800 ℃，以氮气作为载气，空气流量为20 L/min的条件下，在STA6000同步热分析仪中进行非等温测试。

2 结果与讨论

2.1 活化对TG-DSC曲线特性的影响

利用同步热分析仪温控程序得到样品1和样品2在10、15、20 K/min三种升温速率下的TG-DSC曲线(见图4和图5)。

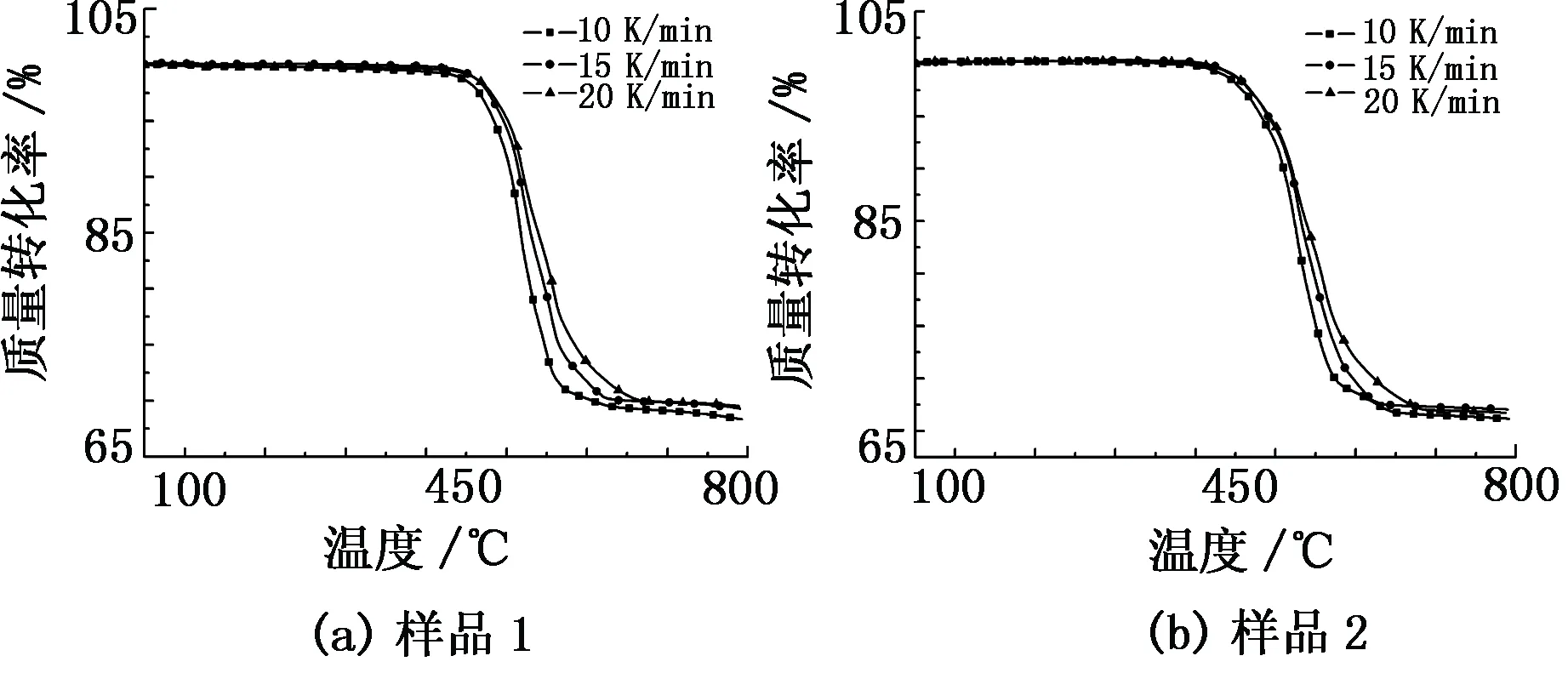
图4 三种升温速率下的TG曲线

图5 三种升温速率下的DSC曲线

采用Pyris Manager软件对机械活化前后黄铁矿样品的TG-DSC曲线进行分析，得到样品1和样品2在10、15、20 K/min三种升温速率下的特征参数(见表2)。

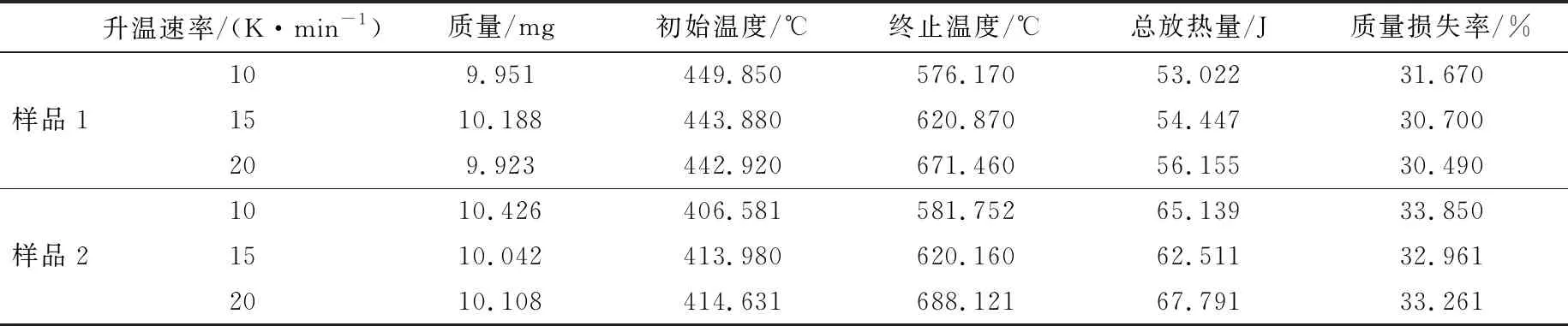
表2 样品1、样品2在三种升温速率下的特征参数

由表2可知：机械活化后的黄铁矿样品初始温度均低于未活化的黄铁矿样品，而两者终止温度相近，主要因为在两者平均粒径相近的条件下，经行星球磨机机械活化后的黄铁矿结构发生了改变，在黄铁矿晶体内部机械能以其他的形式存在，这导致机械活化后的黄铁矿样品更易发生氧化自燃反应，这与文献[6]的研究结果一致；机械活化后黄铁矿样品的质量损失率和总放热量均大于未活化的黄铁矿，这说明在平均粒径相近、质量相同的条件下，黄铁矿经机械活化后的氧化自燃反应更加彻底，氧化产物的转化率增大。

2.2 活化对黄铁矿热反应动力学影响分析

2.2.1 基于Malek法推断最概然机理函数

黄铁矿的氧化自燃反应属于非均相反应，反应过程中包含多个平行、连续的基元反应，但为了便于分析黄铁矿的氧化自燃反应的动力学规律，通常将复杂的反应过程简单化，采用单一的反应机理函数模型描述黄铁矿氧化自燃过程。本文将根据几种常见的反应动力学机理函数的积分式和微分式[16](见表3)，结合Malek法[17]推断机械活化前后黄铁矿样品氧化自燃反应的最概然机理函数。

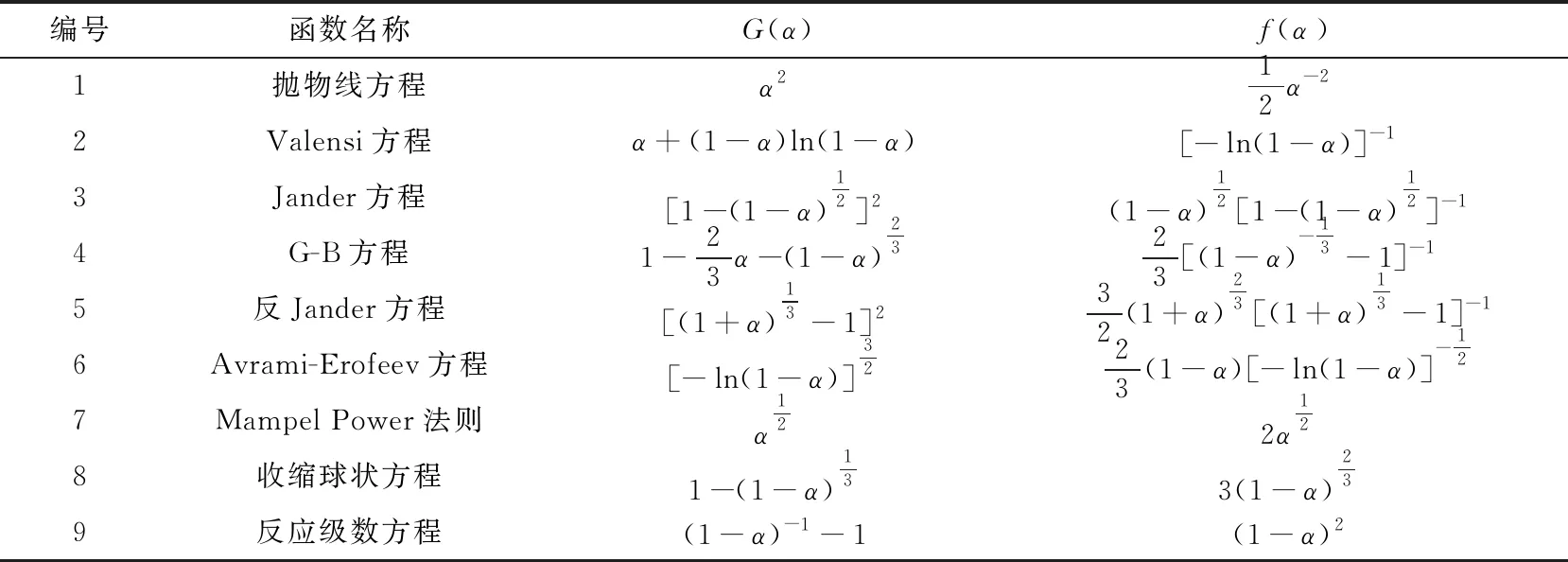
表3 常见的机理函数

(1)

将人为数据：αi，y(αi)，i=1,2,…和α=0.5， 代入式(1)，得到y(α)-α关系曲线，视其为标准曲线。

(2)

将实验数据：αi，Ti，(dα/dt)i，i=1,2,…和α=0.5，T0.5,(dα/dt)0.5代入式(2)，作y(α)-α关系曲线，视其为实验曲线。

若标准曲线与实验曲线偏差最小，则认为该标准曲线对应的机理函数为最概然机理函数。

以上公式中涉及的T为温度，α为反应转化率，i为选取的转化率数量。

将表3中9种常见的机理函数的微分形式f(α)和积分形式G(α)代入式(1)，计算得到标准曲线；将样品1和样品2的实验数据代入式(2)，得到样品在10、15、20 K/min三种升温速率下的实验曲线。运用Origin软件计算实验曲线和标准曲线的偏差，根据偏差的大小确定最概然机理函数。

以未活化的黄铁矿样品1在10、15、20 K/min三种升温速率下的实验数据为例进行计算，其y(α)-α实验曲线和标准曲线的对比见图6。

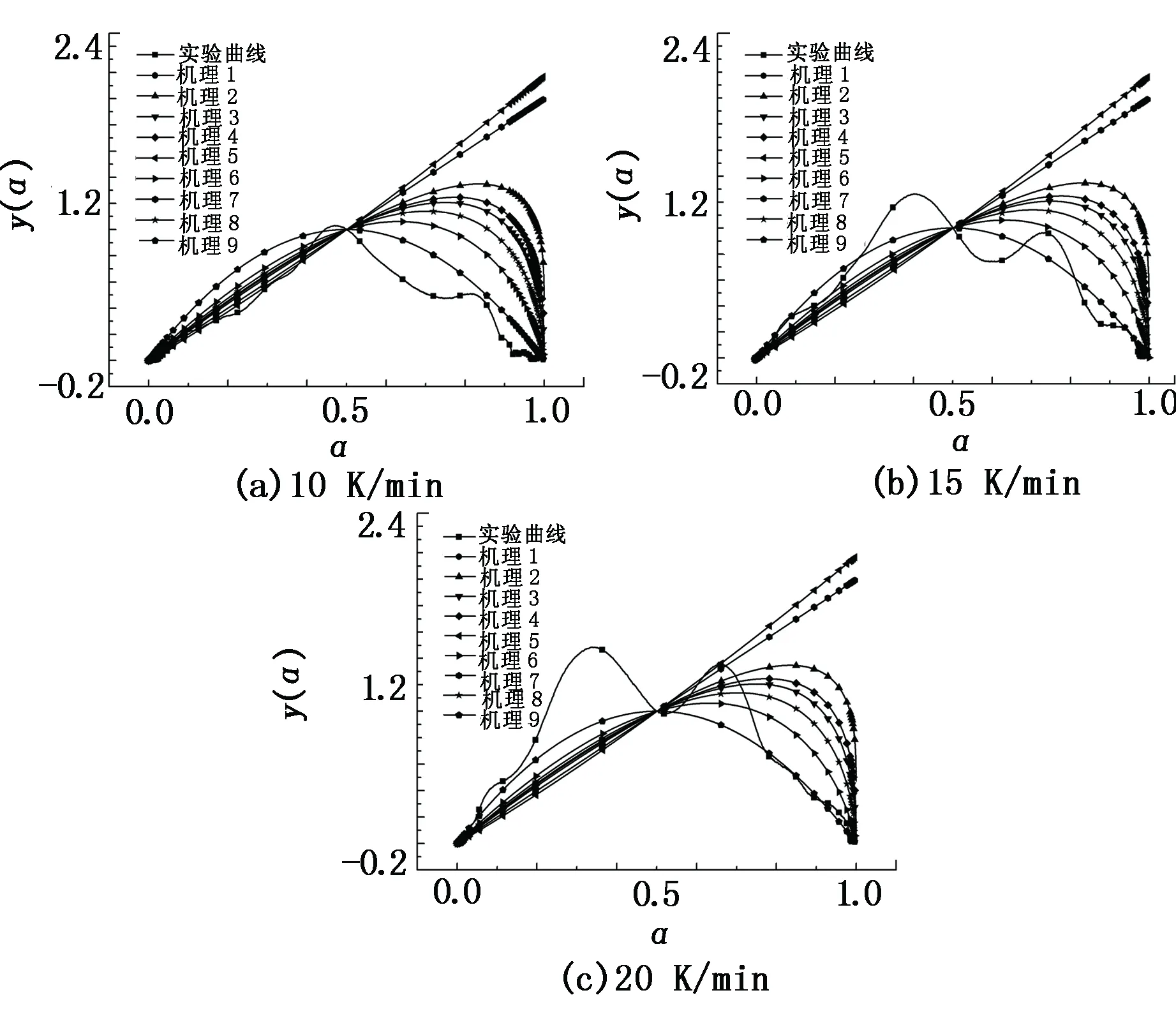
图6 样品1在三种升温速率下的y(α)-α曲线

由图6可知，样品1在三种升温速率下得到的实验曲线与机理函数9的标准曲线偏差最小，且偏差值随着升温速率的增大而减小。同理可证，对机械活化后的黄铁矿样品2在三种升温速率下的实验数据进行处理分析，得到的实验曲线同样与机理函数9的标准曲线偏差最小，表明机械活化前后的黄铁矿氧化自燃反应最概然机理函数均为反应级数方程f(α)=(1-α)2。

2.2.2 基于Achar-Brindley-Sharp-Wendworth法求解动力学参数

Achar微分法的方程为

(3)

式中，E为活化能，A为指前因子，R为气体常数。

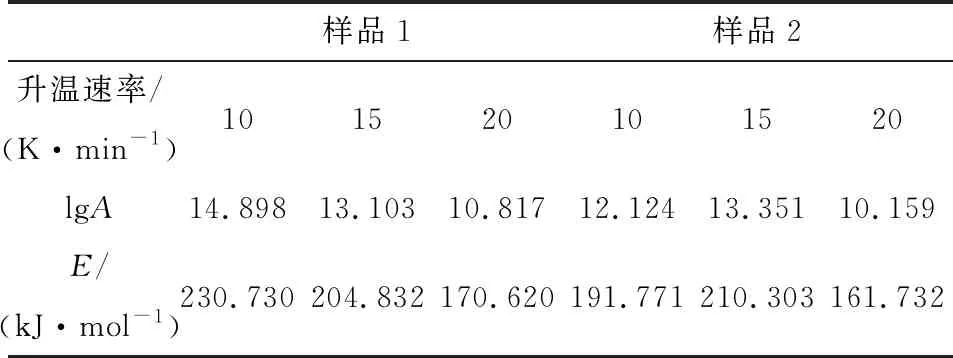
表4 样品1和样品2在三种升温速率下的动力学参数

对比表4中样品1和样品2的活化能可知，机械活化后黄铁矿在10、20 K/min升温速率下的活化能较未活化的黄铁矿小，而在15 K/min升温速率下两者活化能相近，表明在平均粒径相近的条件下，机械活化后的黄铁矿更易发生氧化自燃反应，即黄铁矿经机械活化后常态分子转化为活跃状态的分子，继而发生反应所需要的能量相比未活化的小，这与文献[6]研究结果一致。且样品1和样品2平均粒径相近，在排除粒径对黄铁矿活化能影响的前提下，机械活化后的黄铁矿活化能降低的主要原因是在机械力的作用下黄铁矿晶格发生畸变、晶粒粒径减小。

2.2.3 动力学模型验证

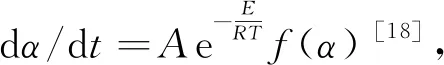
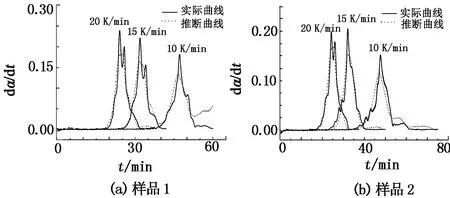
图7 三种升温速率下实际曲线与推断曲线的比较

由图7可知，用所求的最概然机理函数得到的计算曲线与实验曲线吻合度较好，且计算曲线和实验曲线随着升温速率的增加两者的偏差减小，该结果验证了反应机理函数f(α)=(1-α)2的准确性，表明该机理函数反应速率方程可以合理描述机械活化及未活化的黄铁矿的氧化自燃反应过程。

3 结论

a.通过对比机械活化前后的黄铁矿在10、15、20 K/min三种升温速率下的TG-DSC曲线，发现在平均粒径相近、质量相同的条件下，机械活化后的黄铁矿反应的初始温度较低，而最终转化率较高。

b.用Malek法推断出机械活化及未活化的黄铁矿的最概然机理函数均为f(α)=(1-α)2，且升温速率越高，标准曲线与实验曲线偏差越小，即反应机理为f(α)=(1-α)2的可能性越大。用Achar微分法分析相近粒径条件下活化及未活化的黄铁矿的动力学参数，排除了机械活化后粒径对黄铁矿的影响后，活化能相差较小，其主要原因是机械作用导致晶格发生了变化。

c.通过动力学模型验证发现，用Malek法求得的机械活化及未活化的黄铁矿的最概然机理函数对应的计算曲线与实验曲线吻合较好，表明该方法得到的机理函数可以合理描述机械活化及未活化的黄铁矿的氧化自燃过程。