基于AHP-正交试验模型围岩稳定性影响因素数值模拟研究

李 路

(上海勘测设计研究院有限公司，上海 200434)

随着中国水利水电事业的迅猛发展，地下工程建设规模的不断扩大，特别是水工隧洞得到了前所未有的发展，同时遇到的地质条件也越来越复杂，隧洞施工也出现了大量工程地质灾害问题，而围岩稳定性问题便是其中最突出的一种，因此研究围岩稳定性影响因素则变得尤为重要，对设计引水隧洞布置方案，制定合理的支护措施等提供技术支持。

影响围岩稳定性的因素多种多样，各种围岩分类所考虑的因素，选取的定性、定量指标也各有侧重，总体上来说不外乎地质因素和工程因素两大类[1]。地质因素主要包括岩石及岩质类型、岩体的结构类型和完整程度、地质构造、地下水状态、初始地应力状态等。工程因素主要包括洞室的轴线方向、断面形状及尺寸、洞室间距，以及施工开挖方法、爆破方式等。李晓静等[2]在研究大型地下洞室围岩稳定性因素时，通过数值模拟计算，建立了影响地下洞室稳定性的层次分析模型。薛彦平等[3]采用层次分析法对深部巷道围岩稳定性影响因素进行了评价分析。王迎超等[4]通过统计分析，得到隧洞塌方的主要影响因素，然后引入层次分析法，对隧洞塌方的影响因素进行了分析与权重计算。马俊杰等[5]综合熵权和层次分析法对围岩大变形影响因素进行权重求解，并结合专家评分法构建了围岩大变形烈度预测模型。方诗圣等[6]针对围岩稳定性影响因素的不确定性和模糊性问题，在云模型的基础上，结合熵权法建立了考虑多种地质和水文因素的稳定性评价模型，并实现围岩稳定性分类。凌标灿等[7]运用三维数值模拟分析了巷道断面形状、开挖面距离以及开挖顺序等工程因素对巷道围岩稳定性的影响。冷先伦等[8]在研究影响地下洞室群围岩稳定性时通过引入遍布节理模型，同时考虑岩块和节理属性，使研究更加符合岩体状态和工程实际。耿萍等[9]在研究影响隧洞围岩稳定性时，考虑了不同断层倾角的因素。就目前而言，围岩稳定性影响因素研究还不够全面且因素分析方法还存在不足，因此笔者综合考虑了区域地质和工程因素，采用正交试验设计数值模拟方案，通过极差分析方法获得围岩稳定性影响因素主次关系，进而采用层次分析法进行因素确权，从而消除主观判断影响，增加一致性检验的满意度，同时用递阶层次结构对围岩稳定性影响因素进行了表达，使分析结果更加可信。

1 工程地质概况

某水电站采用引水隧洞方案。引水隧洞长约13.27 km，沿线两岸山体雄厚，谷坡陡峻，属典型的中高山峡谷地貌，从上游到下游有多条冲沟切割。沿线地层岩性主要为眼球状片麻岩，局部夹有片岩，岩体完整性较好，多呈块状、次块状。围岩类别以Ⅱ、Ⅲ类为主，局部Ⅳ、Ⅴ类，基本具备成洞条件。岩石主要物理力学参数范围见表1。

表1 岩石物理力学参数

2 正交数值模拟试验

2.1 数值模型的建立

采用有限差分软件FLAC3D建立模型，对隧洞开挖过程中的围岩变形破坏位移进行计算机模拟。为了简化计算过程，将模型概化为单一均质岩体，应用Mohr-Coulomb本构模型，模型大小为50 m×50 m×50 m，模型X方向的边界采用约束X方向单向位移的边界条件，Y方向的边界采用约束Y方向单向位移的边界条件，底部边界采用固定约束边界，表面为自由边界，通过在模型顶部施加不同荷载来模拟不同埋深状态下应力大小，数值模拟计算模型见图1。

2.2 数值模拟方案设计

正交试验法是利用数理统计学与正交性原理，采取部分试验来代替全面试验的方法，它具有“均衡分散性”和“整齐可比性”的特点，能够较全面地反映各因素、各水平对指标影响的情况[10-12]。

由于引水隧洞跨度很大，因此区域内岩体的弹性模量、黏聚力与内摩擦角等重要参数差异也很大；由于不同区域的地层分布和厚度均不同，所以不同区域的引水隧洞埋深也不同；在满足工程布置和施工要求的情况下，隧洞横断面尺寸的确定关系到隧洞的造价和工程效益，尤其对于长距离的水工隧洞，其投资往往占整个工程投资的较大比重。隧洞洞径越小，在相同设计条件下，隧洞工程主体投资越小，但相应的隧洞水头损失就越大，电站发电水头就越低，从而导致电站发电量的损失及经济效益的减少。为了定量描述这些影响因素对隧洞围岩稳定性的影响，采用正交试验原理对地质因素岩体变形参数弹性模量E、岩体强度参数黏聚力C和内摩擦角Φ、工程因素隧洞埋深H和隧洞半径R等5个影响因素来进行数值模拟。数值模拟正交试验变量见表2。

表2 数值模拟正交试验变量

2.3 数值模拟结果分析

根据标准正交试验表选取L16(45)正交试验表，采用数值模拟软件进行16个工况模拟试验，得到隧洞顶部竖向位移和隧洞腰部水平位移(模型监测点所在平面为Y=25 m)，其中模型4的数值模拟结果见图2。

图2中，由Z方向位移云图和位移迹象线可知，越靠近隧洞，位移量也越大，但隧洞的不同位置位移量和位移方向是不同的：在隧洞顶部取得最大位移为10.6 mm，方向为竖直向下；隧洞腰部的位移为6.8 mm，方向为水平向；隧洞底部的位移为5.8 mm，方向为竖直向上；隧洞底部两侧位置取得最小位移，方向近似与临空面垂直，指向隧洞圆心偏下方。同理，对其他15个数值模拟试验进行分析，正交试验设计及数值模拟结果见表3。

图2 数值模拟结果

3 围岩稳定性影响因素分析

对正交试验数值模拟结果进行围岩稳定性影响因素分析，首先采用极差分析法确定主次因素关系，然后采用层次分析AHP法进行因素确权。

3.1 极差分析法

极差分析法是通过计算各因素在各水平下考察指标的平均值及其极差，以及绘制因素与考核指标的趋势图，分清各因素对考核指标影响的主次顺序以及各因素与考核指标的关系[13]。极差是指一组数据中最大数据与最小数据的差，反映了一组数据的离散程度[14]。极差可作为评价因素显著性的参数，正交试验极差分析法是根据极差值大小来比较各影响因素的重要性等级，极差越大，则该因素越重要，对结果产生的影响也越大，极差最大的因素也就是最主要的因素。极差越小的因素可以认为当该因素在所选用的范围之内变化时，对该指标影响不大。围岩稳定性影响因素极差分析见表4，隧洞顶部竖向位移与水平因素趋势见图3，隧洞腰部水平位移与水平因素趋势见图4。

表3 正交试验设计及数值模拟结果

表4 围岩稳定性影响因素极差分析

由表4可知，影响隧洞顶部竖向位移和隧洞腰部水平位移的主控因素均是隧洞埋深因素，最不重要因素均是内摩擦角因素，但主次因素并不是一样的，影响隧洞顶部竖向位移主次因素为隧洞埋深H>隧洞半径R>弹性模量E>黏聚力C>内摩擦角Φ，影响隧洞腰部水平位移主次因素为隧洞埋深H>弹性模量E>隧洞半径R>黏聚力C>内摩擦角Φ。

图3中，隧洞顶部竖向位移与埋深、半径均呈正比，即埋深越深、隧洞半径越大，隧洞顶部竖向位移也越大；弹性模量随水平因素增大时，其竖向位移先增大后减小，且当处于2水平时，其竖向位移量最大；黏聚力和内摩擦角均是随水平因素增大时，其竖向位移先减小后增大，且在3水平时竖向位移量最小。

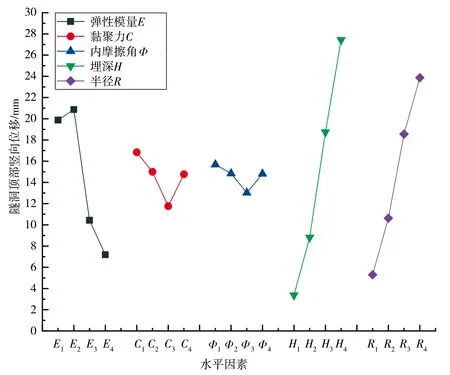
图3 隧洞顶部竖向位移与水平因素趋势

图4中，隧洞腰部水平位移在各因素水平下变化趋势整体与隧洞顶部竖向位移在各因素水平下变化一致，但位移量较小，整体来看，区域内影响隧洞竖向位移因素离散程度较影响隧洞腰部水平位移的因素更大。

图4 隧洞腰部水平位移与水平因素趋势

3.2 层次分析法

层次分析法是美国运筹学家Saaty于20世纪70年代提出的，其将与决策有关的元素分解成目标、准则、方案等层次，在此基础上进行定性和定量分析，具有系统、灵活、简洁的优点[15]。

根据极差分析结果进一步采用层次分析法确定权重，这一方法消除了传统单一采用层次分析法具有主观判断的影响，又弥补了极差分析不能用递阶层次结构表达评价对象的复杂关系，最终得到最低层相对于最高层的重要程度的权值。

3.2.1构建层次结构模型

根据隧洞数值模拟，把确定各影响因素的权值作为层次分析的目标层；把隧洞关键点位移最为层次分析的准则层；把隧洞位移影响因素作为层次分析的方案层，主要包含五大影响因素：弹性模量E、黏聚力C、内摩擦角Φ、隧洞埋深H、隧洞半径R。层次结构模型见图5。

图5 层次结构模型

3.2.2构建判断矩阵

按照各因素对隧洞顶部竖向位移量和隧洞腰部水平位移量的贡献大小，根据各因素位移结果分析极差值进行相互比较判断，就各因素相对重要性bij列出判断矩阵B，即：

(1)

式中bij——bi相对于bj的重要程度。

以定量化的判断矩阵表述各因素的相对重要程度，相对重要性以1～9标度，两两比较，其判断矩阵标度定义[16]见表5。

表5 判断矩阵标度定义

影响引水隧洞顶部竖向位移和影响引水隧洞腰部水平位移判断矩阵分别为B1、B2：

3.2.3一致性检验

对判断矩阵的一致性进行检验，一致性指标用CI计算，CI越小，说明一致性越大。用最大特征值对应的特征向量作为被比较因素对上层某因素影响程度的权向量，其不一致程度越大，引起的判断误差越大。

CI=(λmax-n)/(n-1)

(2)

式中λmax——最大特征值；n——矩阵阶数。

当CI=0时，有完全的一致性；CI接近于0时，有满意的一致性；CI越大，不一致越严重。为衡量CI的大小，引入随机一致性指标RI，随机一致性指标RI和判断矩阵的阶数有关，其对应关系见表6。

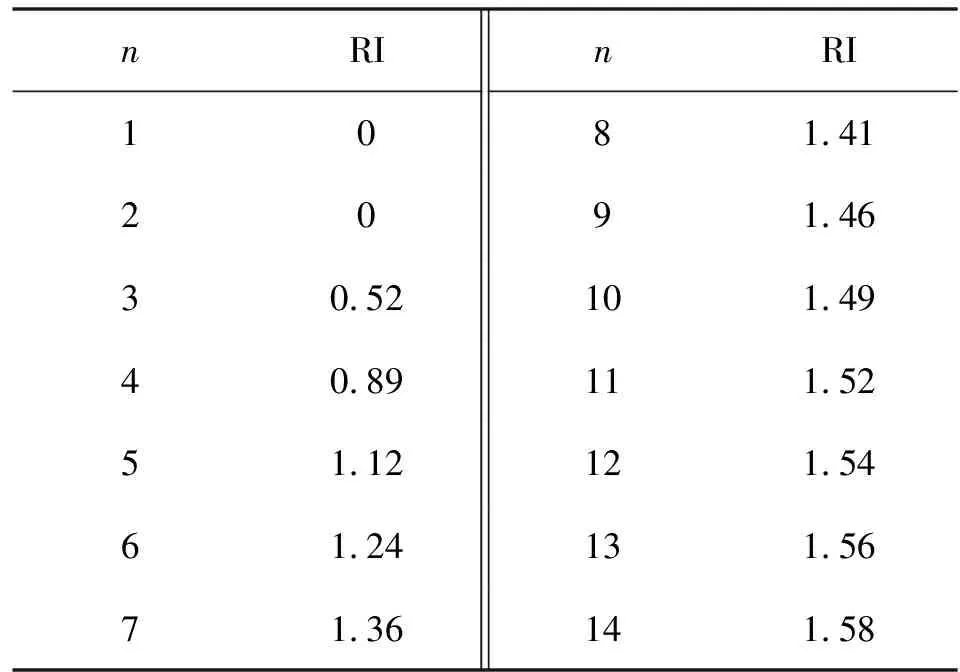
表6 平均随机一致性指标

考虑到一致性的偏离可能是由于随机原因造成的，因此在检验判断矩阵是否具有满意的一致性时，引入一致性比率CR。

CR=CI/RI

(3)

当CR<0.1时，则认为判断矩阵通过一致性检验，否则应对判断矩阵作适当的修正。

计算可知：判断矩阵B1和B2的最大特征值λmax均为5，一致性指标CI均为0，随机一致性指标RI均为1.12，一致性比率CR均为0(小于0.1)，判断矩阵具有完全的一致性，说明评价因素的权重分配是合理的。隧洞顶部竖向位移和隧洞腰部水平位移影响因素AHP层次分析结果见表7。

由表7可知，根据判断矩阵B1得到的最大特征根为5，特征向量W=(0.956,0.294,0.159,2.155,1.437)T，评价指标的权重分配为19.117%,5.871%,3.184%,43.097%,28.731%；根据判断矩阵B2计算得到最大特征根为5，特征向量W=(1.091,0.408,0.228,2.342,0.931)T，评价指标的权重分配为21.820%,8.160%,4.562%,46.832%,18.626%。

表7 AHP层次分析结果

4 结论

a)本文以某水电站引水隧洞为研究对象，基于正交数值模拟试验，结合引水隧洞区域内工程地质特征，建立了适合本区域内AHP-正交试验模型围岩稳定性影响因素评价方法。

b)根据正交试验极差分析结果进而利用层次分析法进行因素确权，通过判断矩阵的建立、特征向量求取及一致性检验，确定了5个影响因素的权重，通过定性与定量分析相结合，既消除了主观判断的影响，又用递阶层次结构对围岩稳定性影响因素进行了表达。

c)影响隧洞顶部竖向位移主次因素依次为隧洞埋深H、隧洞半径R、弹性模量E、黏聚力C、内摩擦角Φ，权重分别为43.097%、28.731%、19.117%、5.871%、3.184%；影响隧洞腰部水平位移主次因素依次为隧洞埋深H、弹性模量E、隧洞半径R、黏聚力C、内摩擦角Φ，权重分别为46.832%、21.820%、18.626%、8.160%、4.562%。