迭代法解析核信号成形电路数字解

李乐赛 周建斌 洪 旭 马英杰 刘 易

（成都理工大学核技术与自动化工程学院 成都610059）

常见核领域电路的公式推导大都采用拉普拉氏变换［1］，缺点是既不够普遍，不适用于所有的电路，且推导过程复杂。本文采用数值解的方法来推导核领域中常见的C-R、R-C、S-K滤波电路，但并未采用递归的方法，递推法需设定恰当的输出电压初值，才能得到理想的递归值［2-7］。实测条件下初值未知，不恰当的初值设定可能导致错误。而迭代法初值为假设值，对结果无影响。本文采用数值解中的迭代法推导电路的输出信号，得到的输出电压值精度可调［8-9］。迭代法与递归法得到的结果基本一致，误差精度上高于10-11，且迭代解与解析解的误差由数据采样率决定，故通过提高数据采样率能降低差值，误差可控［2］。

1 Jacobi迭代法

Jacobi迭代法的计算过程中系数矩阵A始终不变，容易并行计算。对于线性方程组：

式中：A为非奇异矩阵；x为解向量；b为常数向量。

解Ax=b的Jacobi迭代法的分量形式为［8］：

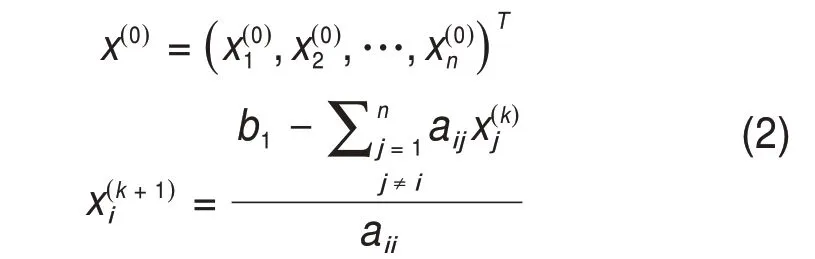
i=1，2，…，n；k=0，1，…迭代次数

2 R-C、C-R成形模型迭代法

2.1 R-C积分电路

R-C积分电路是核电子学电路中常用的滤波电路，图1（a）为R-C积分电路，输入信号为Vin、输出信号为Vout。基于基尔霍夫电流定律（Kirchhoff's Current Law，KCL）该电路可以等效成式（3）。

电容属于抗性器件，涉及到瞬态分析，可通过隐式欧拉法将微分化为差分。令极短时间Δt，则：

Vn和Vn-1分别代表nΔt和（n-1）Δt时刻电容两端电压值，式（4）化成：

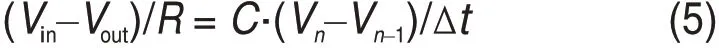
式（5）可化为：

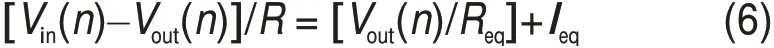
式中：Req=Δt/C，Ieq=C·(Vn-1)/Δt，即将电容看作一个电阻并联上电流源，等效模型如图1（b）所示［10］。

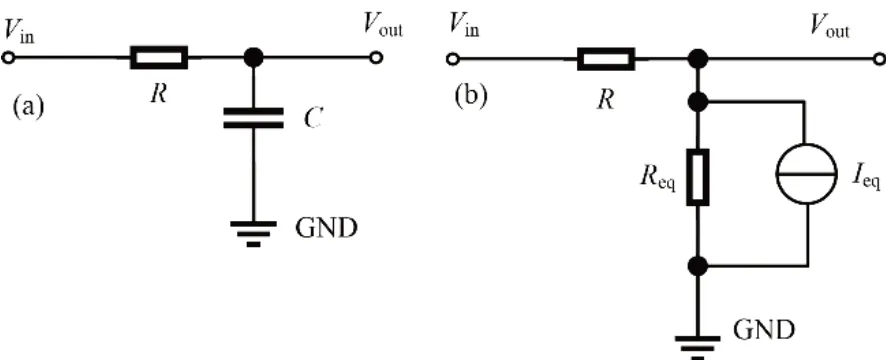
图1 R-C积分电路(a)与等效电路(b)Fig.1 R-C integral circuit(a)and its equivalent circuit(b)

整理得：

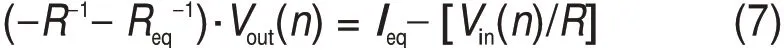
已知采样步长时间Δt，假设初始电压Vout（0），设置迭代精度e，通过某时刻输入信号Vin（n）能迭代出满足精度要求的输出电压Vout（n）。

2.2 R-C积分电路仿真

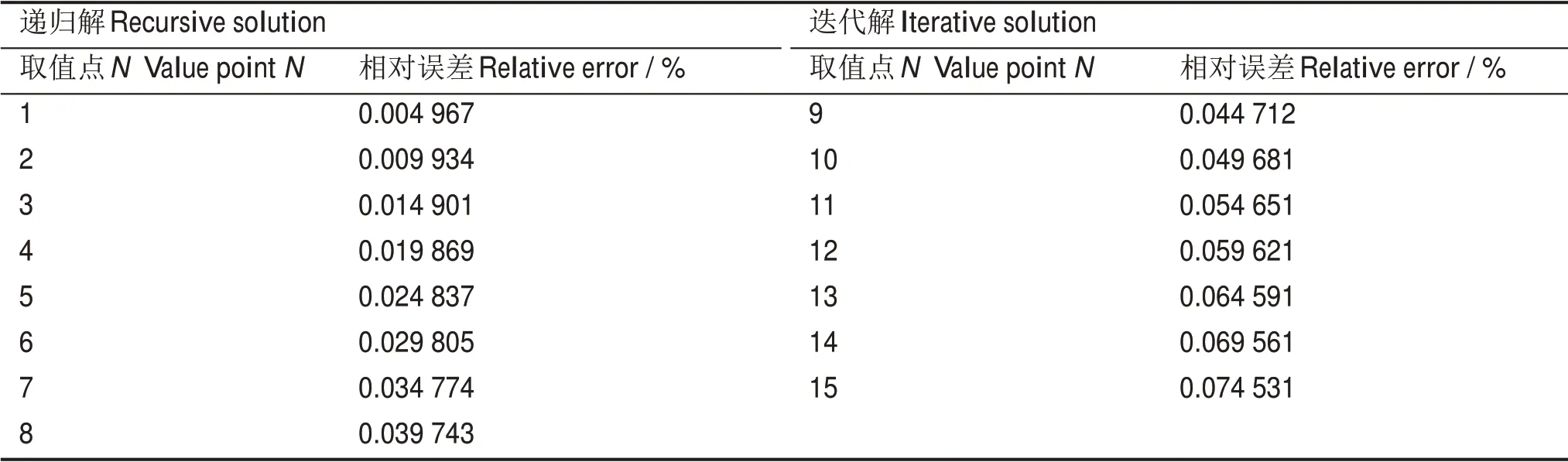
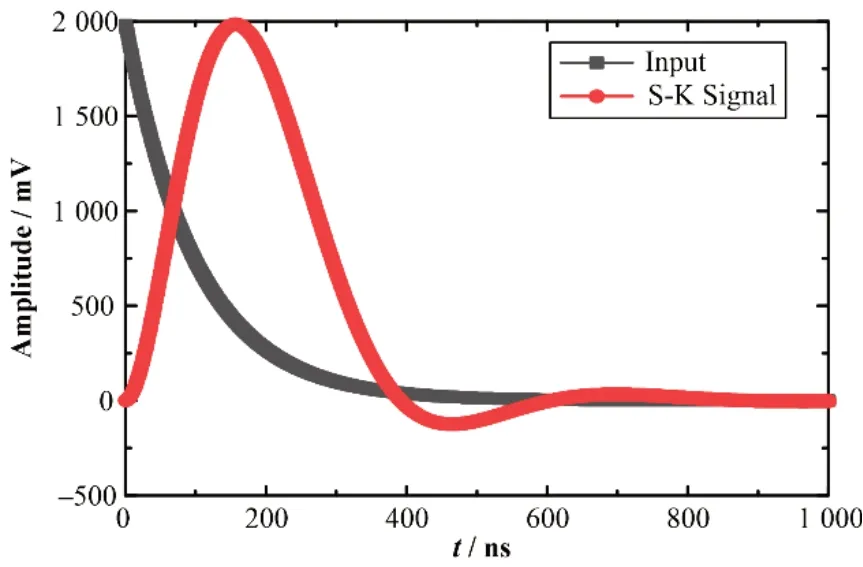
用Jacobi迭代法对式（7）仿真。用标准负指数衰减信号模拟核信号，表达式为y=2 000e（200-t）/50（t≥200）和y=0（0

图2 R-C仿真波形Fig.2 Simulation waveform of R-C circuit

由数值解公式Y（n+1）=［K·Y（n）+X（n+1）］/（1+K）可知［1］，K=（R·C）/Δt，输出信号波形随常数K值而改变，图2说明迭代法得到的输出信号同样符合此规律。表1对数值递归解和迭代解进行误差比较，结果几乎一致，误差量级在-13次方，说明迭代法的解误差较小。Vout（0）为假设值不影响迭代结果。采样步长时间Δt=50 ns、K=100、输入幅值为2 000 mV的阶跃信号。采用递归法，令初始输出电压Vout（0）为0时，得到的输出信号如图3（a）所示；令Vout（0）为2 000时，效果如图3（b）所示，输出信号错误地与输入信号相重合。而采用迭代法，初值Vout（0）为0、2 000时，得到的输出信号如图3（c）、（d）所示，皆可得到恰当波形。

图3 初值对递归法和迭代法的影响对比Fig.3 Comparison of the effects of initial values on recursion and iteration

表1 递归解和迭代解差值Table 1 Difference between the recursive solution and the iterative solution

可见，数值递推法在输出电压Vout（0）取值不恰当时，无法得到正确的输出信号，因此该方法不利于实测信号的处理，而迭代法不受初值Vout（0）影响，能够有效地解决这一不足。

2.3 C-R微分电路

C-R微分成形电路是核信号处理中的常用电路。图4（a）是一个C-R微分成形电路，电容同理等效转换为图4（b）模型［10］。图4（b）所示电路同§3.1的分析方法通过节点电压法可以得出等式（8）。

图4 C-R微分电路(a)与等效电路(b)Fig.4 C-R differential circuit(a)and its equivalent circuit(b)

根据式（8）可以迭代出任意时刻的输出电压值。当输入信号为阶跃信号时，dVin/dt为0，易推导C-R微分电路解析式（9）。

说明输入为阶跃信号得到的C-R电路输出信号是一个负指数衰减信号，常数K是Vin的初值，RC是输出信号的成形时间常数。在K=0.01，对式（9）理论值和数值迭代解作误差分析。

表2列出了在采样步长时间Δt=50 ns下，迭代解和解析解间的误差小于0.1%，且迭代解具数值解特性，都随采样步长时间Δt精度的提高而改善。在Δt=5 ns时，即K=0.001，误差下降到0.001%左右，可验证迭代法的可行性。

表2 迭代解和解析解相对误差分析Table 2 Relative error analysis of iterative solution and analytic solution

图5显示了用迭代法模拟连续的阶跃信号成形，阶跃信号是半导体探测器的前置放大器常见的输出信号。由于信号发生幅值不为定值，无法给定恰当初值，故递推法不适用，宜采用迭代法。

图5 迭代法(a)和递归法(b)对连续阶跃信号的成形对比Fig.5 Continuous step signal forming contrast of iteration(a)and recursion(b)

3 高斯成形模型迭代法

3.1 Sallen-Key滤波

S-K滤波器是常见有源滤波器电路。S-K滤波器有两个典型的电路，即高通和低通滤波器。对于正反馈控制，它具有很大的品质因数［11］。采用S-K滤波器对核信号进行成形，可以用较少的阶数获得高斯波形。低通S-K滤波器的原理图如图6（a）所示。同理，S-K电路等效模型如图6（b）。

图6 S-K低通滤波器电路(a)与等效电路(b)Fig.6 S-K low pass filter circuit(a)and its equivalent circuit(b)

3.2 高斯成形模型迭代法

通过节点电压法对图6（b）所示电路分析，选取三个节点根据KCL建立等式，在这里涉及到放大器的“虚短”和“虚断”性质，正负相电压相等，且无电流流入或流出正负相［1］。从而建立等式：

又因：

得到导纳矩阵：

电压向量：

电流向量：

基于上述矩阵，利用基本迭代法可得输出电压Vout。Δt=50 ns、K=70时，得到波形如图7所示。

图7 S-K低通核信号成形Fig.7 S-K circuit core signal forming

在迭代法中，需要给定精度阀值，当输出值达到该精度时则达到迭代终点，此时输出值即满足精度条件的迭代解。输入信号参数同上，只改变精度值e=10-12、10-9和10-6，如表3所示，输出值和迭代次数有所不同。迭代法精度可根据需要而调节，某些场合下精度要求低，可将精度阀值调低，则迭代次数会随着精度的下降而下降，更迅速地计算出结果；对S-K电路采用Jacobi迭代法，精度可达到10-12，采用Seidel、超松弛法、共轭梯度法甚至能达到更高的精度［8］。

表3 精度对迭代结果的影响Table 3 The influence of precision on iteration results

4 结语

本文采用迭代法研究核领域数字模型，有效解决时域递推法存在的初值问题。以R-C积分电路为例，输出电压初值设置不恰当时，采用递推法会得到不合理的输出电压波形，但迭代法可得到合理的波形。通过R-C积分电路、S-K低通滤波电路误差分析，得出在数值分析中利用迭代法来替代递归法是可行的，设置高精度阀值得到的迭代解几乎等同于递归解。C-R微分电路误差分析说明误差值随数据采样率的提高而降低，表明采用迭代法研究数字电路是可行的。