面向残余应力控制的高温合金铣削刀具几何参数优化方法*

朱卫华，王宗园，周金华，路超凡

（1.西北工业大学，西安 710072；2.海装驻西安地区第五军事代表室，西安 712101）

GH4169 是一种极难加工的金属材料，在切削过程中切削力大、温度高，容易发生塑性变形，且已加工表面残余应力常为拉伸应力[1]。上述问题会影响构件的残余应力分布状态，造成构件局部应力集中，导致表面裂纹的萌生与扩展，进而影响构件的使用性能[2]。

在高温合金切削加工过程中，残余应力的分布状态与刀具性能有着密切的联系，而可供选择的刀具材料主要为硬质合金，因此研究刀具结构对高温合金铣削加工性能以及残余应力分布的影响是十分必要的。Yen 等[3]通过有限元分析结合正交试验的方法，初步研究了刀尖形状对残余应力、应变、切削力、切削温度的影响。Lo[4]利用有限元法研究了刀具前角对残余应力、切屑的形成以及工件最后的表面粗糙度的影响。Zong 等[5]采用有限元方法研究了刀具后角对残余应力的影响，并对刀具几何参数进行优化，发现当后角取为6°时，残余拉应力达到最小，而当后角取为9°时，残余压应力最小。任军学等[6]针对硬质合金球头刀铣削TC17 钛合金，通过研究刀具参数对残余应力、表面粗糙度、形貌的影响，得到了一组较好的刀具参数。Liu 等[7]研究了刀尖圆角对CBN 刀具车削残余应力的影响，结果表明，刀尖圆角增加及刀具磨损都会使表面残余应力由压应力变为拉应力。Capello 等[8]试验研究了外圆车削C45 和39NiCrMo3 钢的残余应力，认为刀尖圆角与进给量对表面残余应力有主要的影响，切削速度与主前角的影响很小。Jiang 等[9]研究了刀具直径对铣削残余应力的影响，发现采用大直径的铣刀加工可以明显地减小残余拉应力。

本文针对球头多轴铣削过程，使用遗传算法优化的BP 神经网络建立了刀具几何参数对高温合金铣削残余应力影响的预测模型，并利用萤火虫算法对刀具几何参数进行优化，为高温合金航空结构铣削加工提供刀具选择的依据和方法。

1 试验过程

1.1 试件材料

高温合金按基体元素可以分为铁基高温合金、镍基高温合金、镍铁基高温合金和钴基高温合金四大类。GH4169 为以体心立方γ″和面心立方γ′相沉淀强化的镍基高温合金，其化学成分及力学性能如表1和表2所示。

表1 GH4169 的主要化学成分（质量分数）Table 1 Main chemical composition of GH4169 (mass fraction) %

表2 GH4169 力学性能（20℃）Table 2 Mechanical properties of GH4169 (20℃)

1.2 试验方案

试验机床采用FVP-800A 三坐标精密立式加工中心，铣削方式为逆铣，冷却方式为乳化液冷却。采用17种Φ8 硬质合金球头刀进行试验，为了减小刀具磨损对铣削残余应力的影响，每次试验均采用一把全新的刀具。球头铣刀的具体材料与参数为：K44 硬质合金，四齿，直径为8mm，总长为110mm，刃长为12mm，铣削试验时的刀具悬长设置为76mm。根据刀具参数的不同，采用3 因素4 水平正交试验的方法进行高温合金GH4169 铣削试验，如表3所示。

表3 试验因素及其相应水平Table 3 Experimental factors and their corresponding levels

每个试件规划6 个加工区域，斜面与水平面的夹角Φ均为85°，每个区域为37.5mm×20mm 的矩形，以保证每组试验加工区域的条件相同，如图1所示。指定进给方向为x轴，y轴位于加工表面内并垂直于x轴。试验前，对试件进行去应力退火热处理，并且铣掉加工区域距表面0.5mm 深度的硬化表层，分两次进行，铣削深度分别0.3mm 和0.2mm，具体试验铣削参数如表4所示。铣削试验现场如图2所示。

图1 试件实物尺寸Fig.1 Physical size of specimen

表4 铣削参数Table 4 Milling parameters

图2 铣削试验现场Fig.2 Milling experiment site

1.3 残余应力测试及结果

残余应力测试采用PROTO LXRD-MG2000 残余应力测试分析系统。测试采用Mn 靶K Alpha 波段，靶电压25kV，靶电流20mA，布拉格角152°，曝光时间2s，曝光次数10 次，焦斑大小2mm。残余应力测试过程如图3所示，测试结果如表5所示。

图3 PROTO LXRD-MG2000 残余应力测试系统Fig.3 Residual stress test system of PROTO LXRD-MG2000

表5 正交试验残余应力测试结果Table 5 Results of orthogonal experimental residual stress tests

2 遗传算法优化BP 神经网络

神经网络算法通过模拟大量神经元的信息传导方式，将其互联起来组成网络模型。虽然BP 算法有寻优精确的特点，但学习速度慢且为局部搜索的优化方法，可能陷入局部极值，使训练失败。遗传算法具有良好的全局搜索能力，求解时使用特定问题的信息少且具有极强的容错能力，同时选择、交叉和变异都为随机操作，无须确定的精确规则。因此，利用遗传算法优化传统BP 神经网络，既可以减小遗传算法的搜索空间，提高搜索效率，又可以较易地搜索最优解。通过GA 算法优化BP 网络的初始阈值和权值，使网络结构更加科学规范，从而实现更好的预测效果。优化要素主要包括以下内容。

（1）种群初始化。

设初始化的种群C={C1,C2,…,CN}，第n个个体Cn包含BP 神经网络输入层到隐含层的权值矩阵W1n、隐含层到输出层的权值矩阵W2n、隐含层神经元的阈值向量B1n、输出层神经元的阈值向量B2n。

式中，N为种群规模；M为输入层神经元的个数；I为隐含层的神经元个数；J为输出层的神经元个数；ω1nij表示输入层的第m个神经元到隐含层的第i个神经元的初始权值；ω2nij表示隐含层的第i个神经元到输出层的第j个神经元的初始权值；b1ni表示隐含层第i个神经元的阈值；b2nj表示输出层第j个神经元的阈值。将W1n、W2n、B1n、B2n中的所有元素随机赋予某区间上的值。

（2）适应度函数。

神经网络模型确定后，通过训练样本对网络进行训练，系统可预测输出结果，将预测结果与期望的输出结果作差，即误差，将个体适应度值F设置为误差绝对值和：

式中，n表示网络的输出节点数目；yi表示网络的第i个节点期望的输出结果；oi表示第i个节点的预测结果；k为系数。

（3）选择操作。

轮盘赌法作为遗传算法的选择操作，该选择策略实际是依据适应度比例，每个染色体i的选择概率pi可以表示为：

式中，Fi是染色体i的适应度；k为系数；fi为个体适应度值，N1为种群染色体数目。

根据选择概率pi（i=1，2，…，n）把一个圆盘分成n份。在进行选择时，可转动圆盘，若某点落到第i个扇形内，则选择个体i。

（4）交叉操作。

由于染色体采用实数编码，因此交叉操作采用实数交叉的方法，第k个染色体ak和第l个染色体al在j位置的交叉方法可以表示为：

式中，b为随机数，范围是[0,1]。

（5）变异操作。

选取第i个染色体的第j位基因a进行变异操作，可表示为：

式中，amax为基因aij的上界；amin为基因aij的下界；f（g）=r2（1-g/Gmax）2；g为当前迭代次数；Gmax是最大进化次数；r、r2都为随机数，范围是[0，1]。

确定神经网络的合适结构之后，GA 对网络权值和阈值进行初始化，会随机分配权值、阈值向量ω、b值给不同的神经元，输入向量x，经过S 型函数变换后，作为下一层的输入量，最终经过输出层线性函数变化，得到网络模型输出结果σx、σy，其与测量值之间存在误差e，e是ω、b的函数，把16 组训练数据的绝对误差和作为适应度函数。将刀具几何参数范围设为约束条件：前角γ0=[3°，18°]，后角α0=[5°，20°]，螺旋角β=[30°，54°]。

由于过度训练是BP 网络训练面对的主要问题之一，每个依赖其学习能力的神经网络应当避免过度训练[10]。目前通过反复调试程序的方法，不断尝试改变GA 终止进化代数、初始种群规模、交叉概率、变异概率，可以获得合适的神经网络权值阈值，即得到使得16 组训练数据误差和最小的权值ω和阈值b。最终采用的遗传算法主要参数如表6所示。基于GA 优化的BP 神经网络建模流程如图4所示。

图4 GA 优化BP 神经网络流程图Fig.4 Flowchart of GA-optimized BP neural network

表6 遗传算法主要参数Table 6 Main parameters of genetic algorithm

3 工艺参数优化方法

3.1 萤火虫算法

萤火虫算法（FA）是受自然界中的萤火虫通过荧光进行信息交流这种群体行为的启发演变而来的一种新颖的仿生群智能优化算法。萤火虫彼此吸引的原因取决于两个因素，即自身亮度和吸引度。其中，萤火虫发出荧光的亮度取决于自身所在位置的目标值，位置越好目标值越佳。萤火虫的吸引度与亮度，与它们的距离成反比关系[11]。

在萤火虫算法中，萤火虫由于“亮度”不同，受到的“吸引力”也不同，从而产生“位移”，算法的3 个要素：亮度、吸引度和位移[12]，具体定义为：

3.1.1 萤火虫的亮度

（1）相对荧光亮度。

假定在解空间中的位置向量xi和位置向量xj上存在两个萤火虫个体i和j，它们的相对荧光亮度可以表示为：

式中，I0表示最大荧光亮度，也就是自身光源（r=0）处的亮度，与目标函数（适应度函数）关系密切，目标函数越好萤火虫会越亮；γ表示光强吸收系数，设置γ是为了体现荧光随距离增加和传播媒介吸收逐渐减弱的特性，可设为常数；rij为萤火虫i与j之间的空间距离，由笛卡尔距离公式给出：

式中，D是空间维数；xi，m表示萤火虫i在D维空间中的第m个分量。

（2）绝对荧光亮度。

目标函数决定了萤火虫的绝对亮度，因此绝对亮度的取值大小反映了该萤火虫表示的潜在解的好坏，萤火虫的绝对亮度越大，则它代表的潜在解越好。

在具体优化问题中，在位置x处的萤火虫绝对荧光亮度I（x）∝F（x），F（x）为目标函数。将萤火虫i与萤火虫j绝对亮度分别表示为Ii（x）、Ij（x）。若Ii（x）＞Ij（x），则萤火虫i吸引萤火虫j向其移动；相反，萤火虫j吸引萤火虫i向其移动。

3.1.2 萤火虫吸引度

萤火虫吸引度可以表示为：

式中，β0表示萤火虫吸引度的最大值，也就是自身光源（r=0）的吸引度；γ表示光强吸收系数，可设为常数；rij表示不同的萤火虫i与j之间的空间距离。

3.1.3 位置更新

假设Ii＜Ij，即萤火虫j吸引萤火虫i向其移动，萤火虫i位置更新由式（4）决定：

式中，xiold和xinew分别为萤火虫i更新前后的位置向量；α为步长因子，是[0，1]上的常数；rand 为[0，1]上服从均匀分布的随机因子。显然，位置更新公式的第2 项取决于吸引度，第3 项是带有特定系数的随机项。

3.2 目标优化函数

3.2.1 约束条件

建立BP 神经网络模型时，刀具前角、后角、螺旋角是在一定范围内变化的，模型在该范围内才能较为准确地进行预估计算，因此刀具几何参数优化的约束条件为：前角γ0=[3°，18°]，后角α0=[5°，20°]，螺旋角β=[30°，54°]。对于既定的铣削试验，铣削参数被认为是确定的，即进给F、切宽ae、切深ap、切削速度Vc、每齿进给量fz。

3.2.2 目标函数

目标函数F（x）为铣削残余应力的预测模型σx（γ0，α0，β），σy（γ0，α0，β）。最终的最佳适应度即最小拉应力/最大压应力，平均适应度为所有萤火虫个体适应度的算术平均值，则总体优化目标函数可表示为：

3.2.3 优化模型

由于萤火虫算法是搜寻亮度最强的萤火虫的位置，而本文的目标是寻找使残余拉应力最小/残余压应力最大的刀具几何参数。把萤火虫的位置向量用刀具几何参数表示：

则萤火虫的亮度函数可以定义为：

将式（12）代入式（9）和式（10），即可得到萤火虫的吸引度和位置更新函数。具体刀具几何参数优化流程如图5所示。

图5 刀具几何参数优化流程图Fig.5 Flowchart of tool geometry optimization

4 结果与讨论

4.1 残余应力预测结果

经过遗传算法优化后，BP 神经网络的初始权值、阈值已经达到较佳的状态，然后用训练数据集对BP 神经网络的初始权值、阈值进行学习。当达到网络训练要求后，停止训练。最终得到的两个表面残余应力分量模型为σx（γ0，α0，β），σy（γ0，α0，β），将刀具几何参数作为铣削残余应力模型的输入值，经过计算得到预测输出值。图6为训练σx和σy的BP 网络时，GA 的收敛情况。

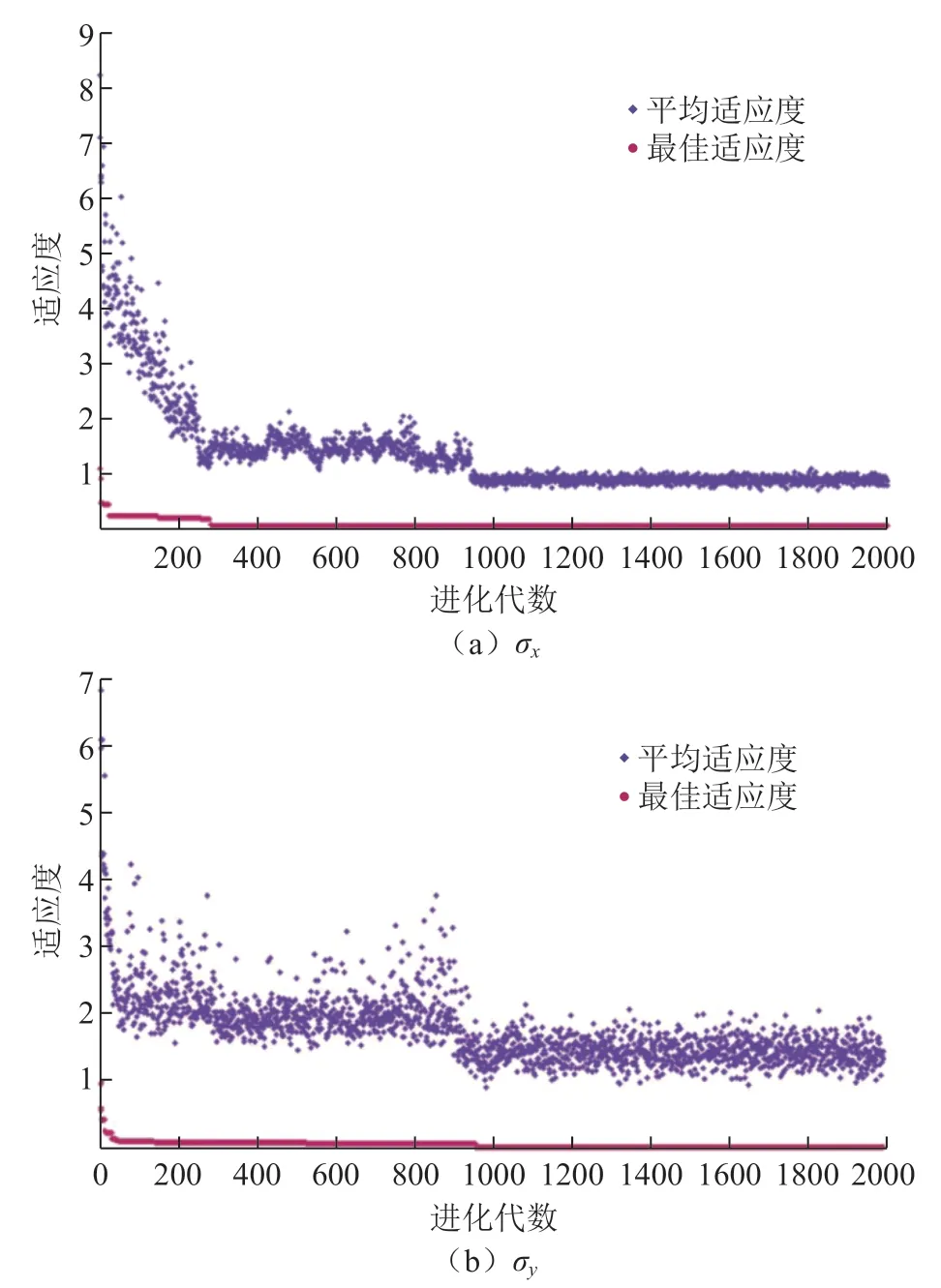
图6 GA 优化σx 和σy 网络的适应度收敛图Fig.6 Convergence plot of adaptation for GA optimized σx and σy network

将σx和σy的BP 网络模型的预测值与相应的试验真实值进行对比，结果如图7所示，其中前16 组分别为两种BP 网络的训练数据预测结果，第17 组为测试数据的预测结果。表7给出了两种网络模型的最终误差统计情况。

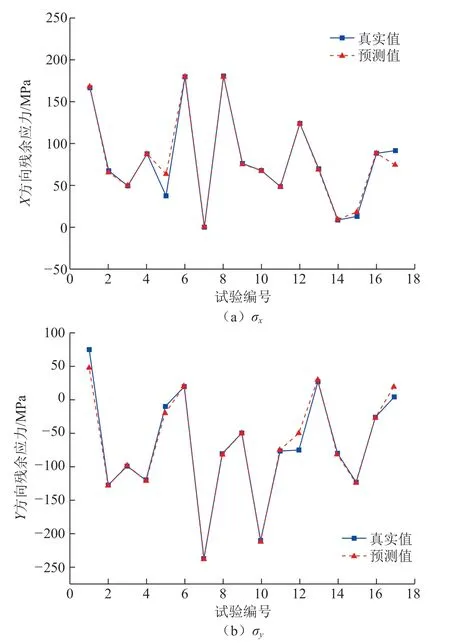
图7 σx 和σy 的BP 网络预测结果Fig.7 BP network prediction results for σx and σy

表7 σx 和σy 的网络模型误差统计Table 7 Network model error statistics for σx and σy

可以看出，模型的预测值和真实值非常接近，训练数据和测试数据的误差很小，网络已被很好地训练。这得益于之前大量调试程序获取的合理的GA 终止进化代数、初始种群规模、交叉概率、变异概率，因此优化的BP 网络初始权值阈值更能满足网络需求。

4.2 刀具几何参数优化结果

经过大量程序测试，萤火虫算法的主要参数最终选定：种群规模为100；迭代次数为1000；步长因子为0.2；光强吸收系数为1；初始吸引度为1。采用萤火虫算法对刀具几何参数进行多目标优化，适应度收敛曲线如图8所示。优化结果如表8所示。应用萤火虫算法对刀具几何参数进行多目标优化，即考虑x方向最小残余应力、y方向最大残余应力。由于刀具在制作过程中存在偏差，同时为了便于工人磨制刀具，因此刀具角度取为优化结果的相近值：前角γ0=6.5°、后角α0=8.5°、螺旋角β=48.5°。

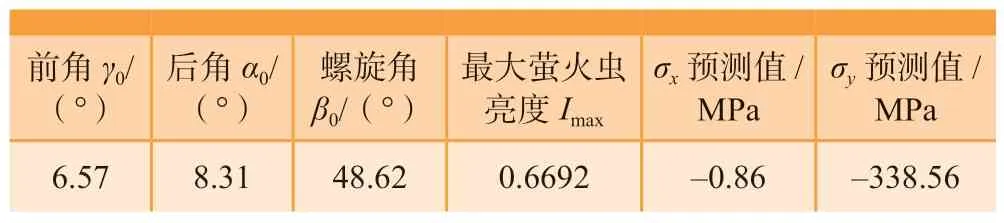
表8 萤火虫算法多目标优化结果Table 8 Multi-objective optimization results of firefly algorithm

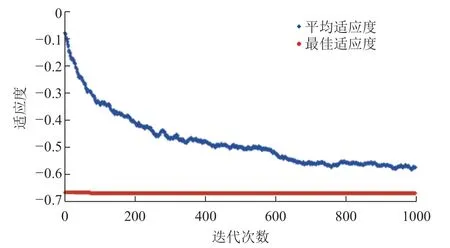
图8 萤火虫算法多目标优化的适应度Fig.8 Adaptation of firefly algorithm for multi-objective optimization

4.3 试验验证

为了证明优化结果的可行性，需要通过实际加工试验对优化结果进行验证。由于刀具在制作过程中存在偏差，同时为了便于工人磨制刀具，因此刀具角度取为优化结果的相近值：前角γ0=6.5°，后角α0=8.5°，螺旋角β=48.5°，刀具其他参数及铣削参数与1.2 节中试验方案相同，加工完后对表面残余应力值进行检测，测量值如表9所示。可知，σx和σy的测量结果和优化结果误差较小，说明使用本文优化的刀具几何参数，可以获得较为满意的表面残余应力σx和σy。

表9 刀具参数优化方案验证结果Table 9 Validation results of tool parameter optimization

5 结论

（1）运用遗传算法优化神经网络的初始阈值和权值，可以使神经网络能更高效准确地对数据样本进行训练，能够提高网络模型的精准度。

（2）基于残余应力的GA-BP 预测模型，应用萤火虫算法对刀具几何参数进行多目标优化。最终综合考虑x方向、y方向残余应力，优选的刀具几何参数为：前角γ0=6.5°、后角α0=8.5°、螺旋角β=48.5°，验证试验结果表明，优化方法与结果可行。