W1型弹条扣压力与疲劳性能的试验研究

余 剑，伍 曾，张景坤，黄新杰

(昆明理工大学建筑工程学院，昆明 650500)

高速铁路不仅是交通运输行业的重要领域之一，还具有国防战略的重要意义。近十年，随着中国高速铁路的快速发展，高速铁路已经成为人们出行选择最频繁的交通方式之一。

W1型扣件技术是中国无砟轨道广泛使用的扣件技术，其工作原理是利用自身产生的弹性变形将钢轨和轨道下部结构连接成一个整体，而高速铁路无砟轨道扣件在承受列车复杂多变的荷载作用下会引发一系列的弹条断裂和锈蚀问题[1-4]。因此，为使列车平稳运行和保护乘客安全，高速铁路无砟轨道扣件的疲劳寿命具有重要的研究意义。

中国对W1型扣件弹条的安装规范按照铁科院于2004年7月公布的WJ-7型扣件组装暂行技术条件进行操作，W1型弹条紧固件安装到位，即弹条中端圆弧位移达到14 mm时其扣压力不小于9 kN，然而目前中国对无砟轨道W1型扣件弹条疲劳寿命对其扣压力影响的研究较少。Thompson等[5]、Byuea等[6]对不同高频作用下各类扣件的力学特性做了试验研究；Casado等[7]通过试验研究了不同扣压力对弹条模态参数的影响；李天夫等[8]对断裂的弹簧钢进行电镜扫描分析，得出弹条原材料在热轧工艺阶段产生折叠造成应力集中而使弹条断裂；黄旭升等[9]对W1型扣件弹条的强度进行了试验和有限元计算，得出弹条的最大应力在弹条后圆弧处；伍曾等[10]对W1型弹条在室温蠕变作用下扣压力的损失进行了试验研究，得出即使在室温条件下，蠕变现象也会使弹条扣压力下降10%左右。目前的研究主要集中在轨下垫板刚度对扣件系统的疲劳影响，但对弹条本身疲劳性能的研究还较少。

首先对W1弹条的原材料60Si2MnA弹簧钢进行静载拉伸试验，得到60Si2MnA弹簧钢的抗拉强度和应力应变关系函数曲线，然后对W1型弹条进行应变电测试验，得出W1型弹条在不同扣压力作用下的应力分布状态，最后对W1型弹条施加三种疲劳荷载工况，研究弹条疲劳性能与扣压力的关系。

1 W1型弹条强度试验

1.1 60Si2MnA静载拉伸试验

为了得到W1型弹条的常规力学性能，将W1型弹条的原材料60Si2MnA弹簧钢前直端截取一部分进行机械加工，加工试件设计图和试件加工实际试样图如图1、图2所示。将加工好的试验试件于MTS810伺服液压试验机上固定进行拉伸试验，通过在弹簧钢试件上施加的荷载和弹条产生的拉伸变量就能绘制弹簧钢的应力-应变曲线，如图3所示。

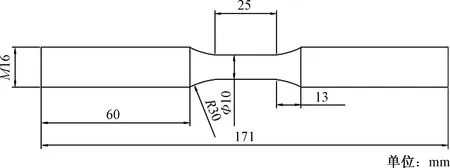
图1 试件设计尺寸

图2 试件加工实际试样图

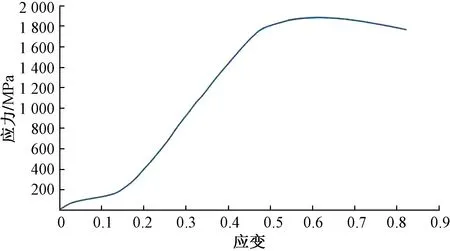
图3 应力-应变曲线

从图3可以看出，60Si2MnA弹簧钢的应力-应变曲线与低碳钢相似，呈4个阶段。第一阶段：应力-应变呈抛物线函数关系，应力随应变增大而缓慢增大；第二阶段：应力-应变呈线性关系，在1 600 MPa左右达到屈服强度，但是没有出现很明显的屈服点；第三阶段：强化阶段，在1 900 MPa左右达到弹簧钢的极限强度；第四阶段：颈缩阶段，应力随着应变的增大反而降低，一直到试件被拉断。

1.2 W1型弹条应变电测试验

为确定弹条最佳扣压力值，对W1型弹条进行应变电测试验，弹条应变花粘贴点位置及弹条各部位名称命名如图4所示，应变花分别粘贴在测点1至测点6上。弹条出厂时表面有一层绝缘的涂料，为使试验结果更精确，试验前需对弹条表面用粗锉刀进行打磨。由于弹条是一个对称结构，正常工作下两边的受力状态基本是一致的，所以只需对弹条一侧进行打磨。打磨完后使用氰基丙烯酸酯黏结剂(520胶)将应变片粘贴在弹条各测点上，本次试验使用的是型号为BF120-2CA的箔式电阻应变片，其敏感栅长度为2 mm、宽为1.3 mm，电阻值为120 Ω，所用的基底材料为酚醛-缩醛，该材料具有良好的柔韧性，方便粘贴，在-30°～+80°其材料性能仍然稳定，电阻应变花粘贴部位及实物图分别如图4、图5所示。

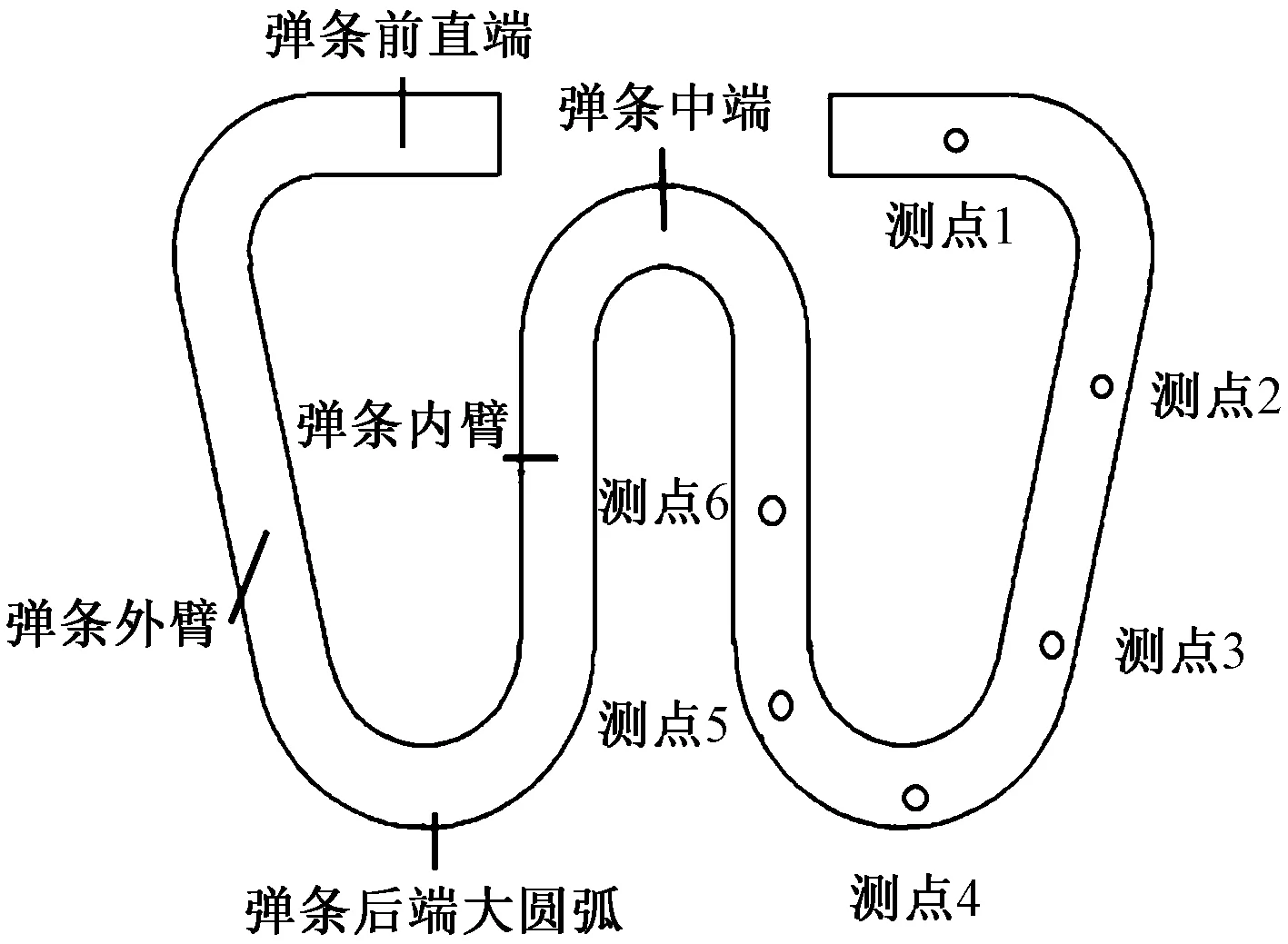
图4 弹条各部位名称及应变花粘贴点

图5 应变花粘贴实物图

在MTS810电液伺服液压试验机上进行W1型弹条应变电试验，如图5所示，试验从0开始加载至35 kN结束，以2.5 kN为加载梯度，应变电测数据从12.5 kN开始记录，同样以2.5 kN为梯度记录数据至35 kN结束。

应变电阻片能测出弹条各测点的应变，但若获得各测点的等效应力值还需要将应变换算为应力，由于弹条形状较为复杂，受力时其各测点的应力方向是未知的，若在弹条任意一测点位置取出一个三维实体单元将存在3个未知的应力分量，因此需要在测点的3个方向上贴上应变片，如图6所示，通过测出这3个方向上的应变来计算出弹条各测点的应力值。

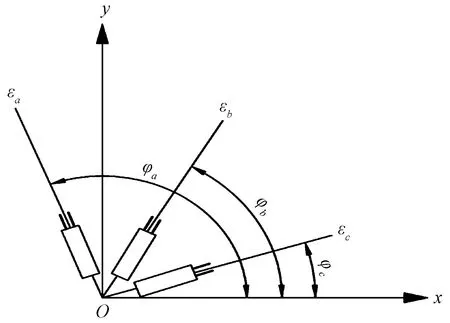
O为测测点；φa、φb、φc为应变片的粘贴角度，分别为90°、45°、0°；εa、εb、εc为对应的每一片应变片所测得的应变，记录3个弹条各测点在90°、45°、0° 3个方向上的线应变εa、εb、εc

由式(1)可解出切应变γxy和x、y方向上的线应变εx、εy。

(1)

式(1)中:φa、φb、φc为应变片粘贴角度，为90°、45°、0°。

由式(1)求出的εx、εy和γxy可通过式(2)计算出最大主应变ε1和最小主应变ε2。

mti(TAEi),maj(TAj)表示mti的制造任务的任务特征集合TAEi与maj的制造活动的任务特征集合TAj进行比较，如果有相同的制造任务特征集合，则该值为True，否则为False。

(2)

再由广义胡克定律式(3)求出最大、最小主应力σ1、σ2。

(3)

式(3)中：E、μ分别为弹性模量和泊松比。

由第三强度理论可知导致材料屈服的主要因素是最大切应力的产生，在平面二向应力状态，最大、最小主应力就是σ1和σ2，则弹条紧固件的屈服准则为

σ3=σ1-σ2

(4)

以MTS810液压机施加的荷载为横坐标，应力为纵坐标，绘制1～3个弹条各测点的应力曲线图如图7所示。

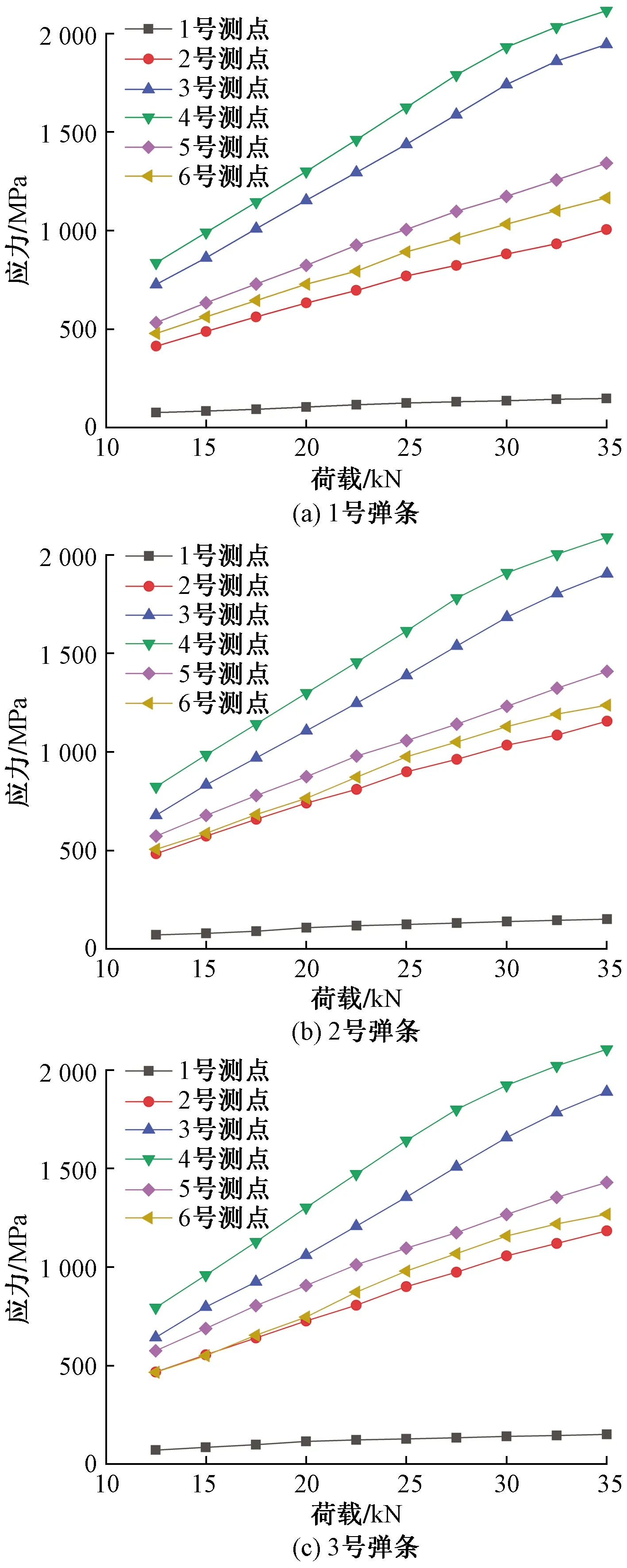
图7 弹条应力-荷载曲线

从图7中可以看出，每个弹条各应力值变化趋势基本一致，当荷载小于25 kN时，1～3号弹条的应力与荷载呈现出线性关系，各测点应力值随着荷载的增大而增大，其中3组弹条1测点的应力值都远小于其他各点的应力值，而4号测点(弹条内侧圆弧)的应力值最大，分别为1 623.8、1 612.8、1 641.2 MPa,达到了弹簧钢的屈服强度，3号测点(弹条圆弧外侧)应力值也偏大，分别为1 436.9、1 387.1、1 354.8 MPa，说明这两处位置出现应力集中。当荷载大于25 kN时，3、4测点的应力值快速增大且增长速度远大于其他测点，在32.5 kN时已经超过了弹条的极限抗拉强度，说明弹条已经开始进入塑性变形阶段。因此，通过试验数据可以确定弹条内侧圆弧是弹条应力最大、最易断裂的位置且弹条的最佳安装预压力为25 kN。

2 W1型弹条疲劳性能试验

W1型弹条疲劳试验同样在MTS810液压试验机上进行，将CFBLZ型压力传感器和D020型位移传感器分别放置在弹条前趾端和弹条中端圆弧下方并接入MTS810伺服液压试验机的控制系统采集压力和位置变化的数值，如图8所示。

图8 传感器实验装置图

由静力试验得出弹条的最佳安装预压力为25 kN，这时弹条测点4的应力值已超过1 600 MPa，达到弹簧钢的屈服强度要求，弹条中端圆弧位移为14.1 mm，弹条扣压力为9.2 kN，已达到WJ-7型扣件暂行技术说明的要求，说明弹条紧固件在25 kN预压力下已达到正常工作所需的扣压力，因此将25 kN设置为压力荷载的平衡位置，疲劳试验采用正弦波作为加载波形，频率为5 Hz，疲劳试验采用荷载位移控制，位移控制方式为使用MTS810伺服液压试验机在W1型弹条上方施加荷载，以0.5 kN作为荷载步长缓慢施加，荷载达到20 kN时记录此时弹条中端圆弧的位移，然后继续以0.5 kN的荷载步长将荷载加载到25 kN时停止并记录此时弹条中端圆弧的位移值，接着继续加载荷载到30 kN并记录此时弹条中端圆弧的位移值，将20、25和30 kN荷载作用下弹条中端圆弧产生的位移分别作为弹条的位移荷载的上值、中间值和下值，这就是弹条在(25±5)kN，即在循环荷载为5 kN作用下的位移荷载控制试验方式。同理，循环荷载为7.5 kN和10 kN的疲劳试验方式也一样。

疲劳位移荷载幅值分别为5、7.5、10 kN，每种循环荷载下取3组试件，每组试件取3个弹条试样进行试验，共计9个弹条试样，即每个位移荷载疲劳试验有3个弹条试件。在平均值为25 kN，循环荷载为5 kN时，循环荷载每循环10 000次作为采集步长记录此时弹条扣压力和中端圆弧位移，7.5 kN和10 kN的采集步长则为2 500次和1 000次。由于每个循环位移荷载试验下3个弹条中端圆弧位移和扣压力变化差值较小，因此取3个弹条的试验平均值绘出弹条中端圆弧达到下值时弹条前趾端所具有的扣压力、中端圆弧位移达到下值时与荷载循环次数的曲线如图9所示。

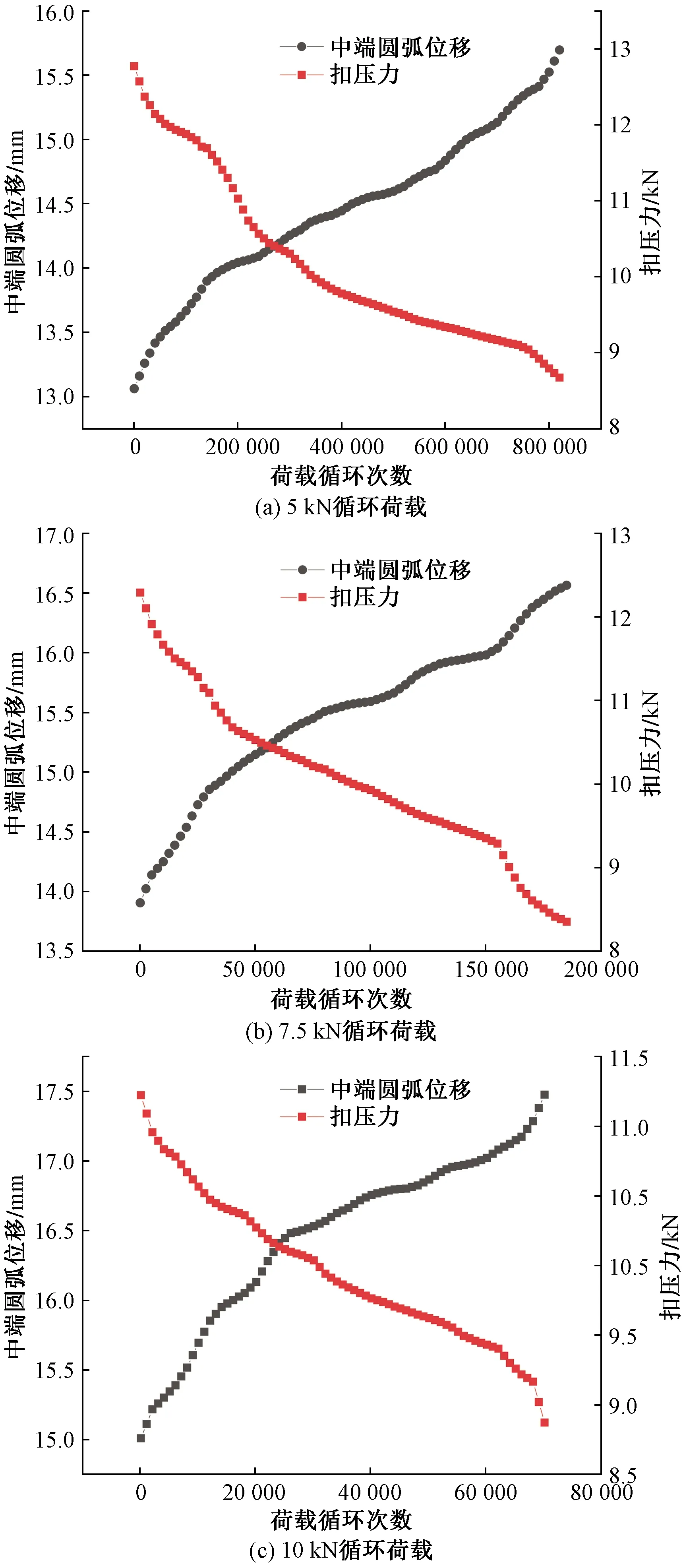
图9 W1型弹条扣压力和中端圆弧位移与荷载循环次数关系曲线

从图9(a)中可以看出，弹条中端圆弧位移从最初的13.062 mm增至15.659 mm时弹条断裂，扣压力从12.771 kN降至8.671 kN时断裂。在5 kN循环荷载作用下，W1型弹条大约能承受80万次循环次数，疲劳寿命满足扣件设计要求。

从图9(b)中可以看出，7.5 kN循环荷载作用下，弹条前期和后期扣压力下降较快，中期下降则比较缓和，扣压力从12.27 kN降至8.352 kN时弹条断裂，根据铁道部公布的《各类扣件技术说明》，这时扣压力已经低于W1型弹条9 kN扣压力的标准。弹条中端圆弧位移增长速度也较5 kN循环荷载快，断裂时位移增大至16.565 mm。

从图9(c)中可以看出，循环荷载10 kN时，弹条中端圆弧位移开始阶段快速上升，仅16 000次荷载循环，中端圆弧位移就从初始的15.01 mm增至16.002 mm，中间阶段增长平稳，经历近4万次荷载循环，也只从16.132 mm增加至17.174 mm，即1.042 mm的位移，但在后期弹条中端圆弧位移又快速变化，仅经历4 000次荷载循环，中端圆弧位移就从1.174 mm增至17.476 mm，说明此时弹条已经达到疲劳极限。

2.1 弹条中端圆弧位移与扣压力的关系

为表征在不同循环荷载作用下W1型弹条中端圆弧位移与扣压力之间的关系，根据试验数据绘制两者的关系曲线并线性拟合，如图10所示。

图10 扣压力与弹条中端圆弧位移关系和线性拟合曲线

从图10可以看出，弹条中端圆弧位移与扣压力呈反向关系，扣压力越大，弹条中端圆弧位移越小，弹条的变形就越小越不易疲劳破坏。依据疲劳试验数据拟合出弹条中端圆弧位移X与扣压力S之间的关系式，循环荷载10 kN时，拟合曲线关系式为X=-1.143S+27.855；7.5 kN时的拟合曲线为X=-0.682S+22.343；5 kN时的拟合曲线则是X=-0.534S+19.887。

3 结论

(1)通过静力拉伸试验可以得到高速铁路无砟轨道W1型弹条的屈服强度为1 600 MPa，抗拉强度为1 900 MPa。

(2)通过应变电测试验得出弹条内侧圆弧处应力值最大，是最易断裂的位置，并确定出25 kN是弹条的最佳安装预压力。

(3)在不同循环荷载作用下，弹条扣压力受其影响较大。5 kN循环荷载作用下随着循环次不断增加，弹条中端圆弧位移逐渐增大，扣压力不断降低，大约82万次荷载循环后弹条断裂；在7.5 kN和10 kN荷载循环作用下，弹条扣压力下降速度明显，7.5 kN荷载循环作用下不到19万次荷载循环弹条断裂，相较5 kN的荷载循环，疲劳寿命下降77%，10 kN荷载循环作用下弹条仅7万次就断裂，疲劳寿命下降91.5%。

(4)由试验得出，在不同循环荷载作用下，扣压力越大，中端圆弧位移越小，反之，扣压力越小，中端圆弧位移越大，两者呈反相关系。