关于加速箱内气球运动的演示实验
路峻岭,顾 晨,任乃敬,马泊一
(清华大学 物理学系,北京 100084)
我国实行改革开放国策之后,中西方文化交流空前活跃,我国注重理论思辨和西方注重从实验出发的特点,在物理学的教学中表现得特别显著. 现在,可以很方便地登录美国物理教学平台,查询与本论文相关的内容[1-3],其对实验的解释虽然未必准确,但把它们引入演示实验教学,对提高学生的学习兴趣,深化对物理原理的理解,很有裨益.
1 实验装置简介
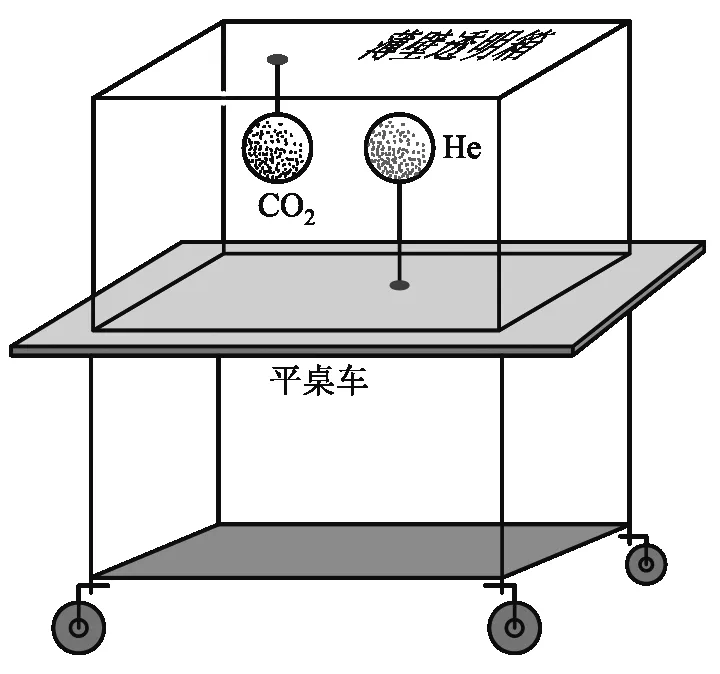
图1 加速箱内气球运动实验简图
本实验装置主要由一个可以加速运动的薄壁透明箱体和箱体内的两个充以不同气体的气球组成,如图1所示.
薄壁透明箱体实际上是一个透明的长方体箱壳,固定在平桌车的桌面上,构成随车一起运动的封闭箱体. 箱体内有封闭的可以随箱体一起运动的空气,在这一箱空气中还设置了两个气球. 一个充入二氧化碳气体,一个充入氦气,令二者的大小差不多,分别用轻细丝线系住,轻细丝线固定于上下箱壁上,并使二气球的中心高度大体相等,且其中心的连线与预运动方向一致. 本实验的主要实验现象是:操作者将静止的平桌车加速推动时,氦气球将取得与平桌车加速度方向相同的加速度;二氧化碳气球将取得与平桌车加速度方向相反的加速度,故可观察到两个气球作相离运动. 如果取向相反的方向加速推动平桌车,则可观察到两个气球作相向运动.
2 实验原理
2.1 网上物理教学平台上的解释
查阅网上相关文章,可以见到一些对本实验的解释[1-3],大都是举一些日常生活的例子,促使学生通过这些具体例子体会本实验所涉及的物理概念,其特点是通俗易懂,但也会出现肤浅误解的情况.例如,加速启动轿车,坐在车座上的人会觉得自己的身体会受到一个推力,使身体向后倾斜,这个力没有施力者,完全是由于人的惯性所产生的,即惯性力.加速启动轿车,轿车内的空气分子也会由于惯性力的作用而向后运动,被车的后壁挡住而堆积在那里形成气压较高的区域,使系在轿车中的氦气球的后部受到的空气的压力较其前部的大,因此氦气球将向车的前部运动.
这样引入惯性力概念的方式值得肯定,但在分析氦气球的运动原因时,只是考虑了车内空气的惯性力,却没有考虑氦气球受到的惯性力;由于惯性力使车内空气运动而产生车内空气气压的不平衡是一个瞬时暂态过程,其解释过分地突出了暂态过程的影响.
还有一个解释涉及到广义相对论爱因斯坦等效原理[3],说是,轿车的突然停止,在轿车(非惯性系)中观测,车内空气和气球都有了一个指向车头的加速度,它与在下山陡坡上静止的车中气体受到的重力加速度相当,结果是氦气球必然将向车的尾部运动.这种解释的特点是:等效原理本质上是非惯性系中惯性力引起的效应;车内空气和氦气球一并考虑;没有明确指出有浮力的作用.
实际上,本实验所涉及的物理原理有:在加速运动中的箱体内的空气、气球内的气体的状态都是近似平衡态的;加速运动流体的引力等效原理;加速运动参照系中的惯性力等等.
2.2 热平衡态近似[4,5]
在均匀且恒定的外部条件的制约下,当一个热力学系统偏离其平衡态时,分子间的相互作用总是使它的状态向平衡态趋近,这一过程称为弛豫过程,其特征时间称为弛豫时间,记为τ.如果所研究的物理过程所需要的时间为Δt,若Δt>>τ,则物理过程所进行的每一个时刻,热力学系统的状态都可以被看作是平衡态,称为准静态.例如,内燃机等热机气缸中活塞运动的加速度通常是很大的,气缸内压缩气体的体积、压强、温度等状态参量都随时间变化.即便是这样,由于Δt>>τ,气缸内气体的状态也被认为是热平衡态(准静态).在本实验中,箱体内的空气、气球内的气体的体积基本上是不变化的,所以,它们的体积、压强、温度等状态参量也都被认为不随时间而变化,是热平衡态,且在加速运动中,封闭气体容器前后壁附近气体分子密度的瞬时变化等在此也可忽略不计.
2.3 等效原理[6-8]
大家熟知,沉浸在相对于惯性系(地面参照系)静止的流体(液体或气体)中的物体,都受到向上的浮力,浮力的大小等于物体排开流体的重量(阿基米德定律).浮力之所以产生,是来源于地球对流体的引力.倘若流体处于地面上的自由落体运动中,则沉浸在其中的物体受到的浮力也就消失了.可见流体中的物体受到的浮力与流体的运动状态相关.在相对于惯性系向上作加速运动(加速度为g)的流体中的物体受到的浮力,与在相对于惯性系静止且有引力(引力加速度为g)的流体中的物体受到的浮力完全相等.也就是说,通过观测沉浸在流体中的物体受到的浮力,无法判断流体是处于静止的引力场中,还是处于相对于在没有引力的惯性系作加速运动中.流体作加速运动与它处于静止的引力场中等效,称为等效原理.
对加速箱内气球的受力分析如图2所示,气球所受重力与细丝线拉力平衡,在竖直方向可以不用去管.在水平方向,设薄壁透明箱连同它内部的空气的加速度为a,气球的体积为V,气球内部气体的密度为ρ,箱内空气的密度为ρ0,箱内空气中的等效引力、气球所受等效浮力F浮如图2所示,且有
F浮=ρ0Va
(1)
注意,F浮是一个真实的力,它是箱内空气对气球表皮各点压力的合力,方向与a相同.

图2 加速箱内气球的受力
2.4 惯性力[6,7,9]
众所周知,牛顿定律只在惯性参照系中成立,设一惯性系为K1系,在K1系中有
F1=m1a1
(2)
若另有一个参照系K2相对于K1系以加速度a0作匀加速直线运动,如图3所示,则由相对运动的关系可知:a1=a2+a0,即a2=a1-a0.而且在非相对论条件下在参照系K2中观测,力和质量都不随参照系的不同而改变(F1=F2,m1=m2).式(2)即可表示为
F1=m1a1=m1(a2+a0)=m1a2+m1a0
(3)
移项可化为
m2a2=m1a2=F1-m1a0=F2-m2a0
(4)
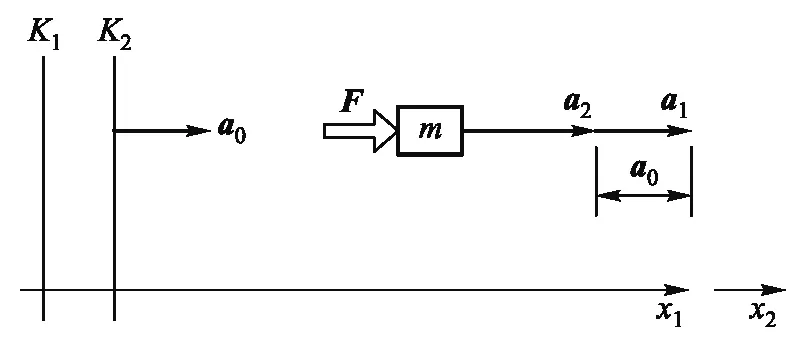
图3 非惯性系中的牛顿定律
式(4)像是可在非惯性系K2中直接应用的牛顿定律,与惯性系表达式的不同就是多出了一项-m1a0,称为惯性力.惯性力不是物体之间真实的相互作用,而是物理学家为了计算形式的方便人为地造出来的一个力,惯性力没有反作用力.在以加速箱为参照系研究箱内气球的运动时必须考虑这个惯性力,它的大小等于气球质量与箱体加速度(非惯性系的加速度)的乘积,它的方向与箱体加速度(非惯性系的加速度)的方向相反.
2.5 具体分析
在加速箱参照系中观测箱内的气球,每个气球都是受到四个力的作用.在竖直方向,重力与细丝线的拉力平衡;在水平方向,气球都是受到等效浮力F浮和惯性力m1a0,两者的方向相反,实验中气球的运动决定于两者谁大谁小.
F浮-ma0=ρ0Va0-ρVa0=(ρ0-ρ)Va0
(5)
在标准状况下(温度为0 ℃,压强为1个大气压)22.4升的空气为29克,22.4升的氦气为4克,22.4升的二氧化碳气为44克.因此,对氦气球来说,ρ0-ρHe>0,上式大于零,氦气球将沿与平桌车加速度相同的方向作加速运动;对二氧化碳气球来说,ρ0-ρCO2<0,上式小于零,二氧化碳气球将沿与平桌车加速度相反的方向作加速运动.换言之,可观察到两个气球在作相离运动,都是相对于加速箱在作加速运动.
3 小结
本实验是典型的必须考虑在非惯性系中分析才比较简洁的问题,同时还要运用等效原理考虑由于箱内空气的加速而产生的水平浮力分量的影响,在操作者沿着两个气球中心的连线的方向,将静止的平桌车加速推动时,两个气球将在等效引力和惯性力的共同作用下作相向或相离加速运动.

