有质弹簧缓慢腐蚀过程中的浸渐不变量及其电学推广

范洪义，陈俊华，吴 泽

(1. 中国科学技术大学 材料科学与工程系，安徽 合肥 230026；2. 合肥工业大学 电子科学与应用物理学院 物理系，安徽 合肥 230026；3. 中国科学技术大学 近代物理系，安徽 合肥 230026 )

量子力学除了有薛定谔的波动力学表述、海森堡的矩阵力学表述(这两种表述被狄拉克视为同一，并发展为符号法)和费曼的路径积分表述外，还有一种常用的是相空间表述[1]，相空间的维数是系统的自由度的两倍.可以说，玻尔-索末菲作用量的量子化(旧量子理论)就是在相空间中进行的.系统动力学的相空间描述的方式有利于“绝热不变量”(或称为浸渐不变量)的讨论.力学系统在外部条件无限缓慢改变(外来干扰)下的进程叫做“绝热”的[2,3,4].相对于外来干扰而言，需要加以量子化的量[5]，从经典力学层面上看必须是对外来干扰不敏感的量.爱因斯坦曾经提出绝热不变量的概念，即在绝热过程中它是一个不变量.玻尔的原子轨道量子化也是受浸渐不变量的影响.

本文想到这样一个物理问题：现实生活中充满风雨阴晦，金属弹簧在空气和雨水浸蚀下缓慢腐蚀，刚度逐渐变小，或说劲度系数逐渐变化.于是就产生了一个有趣的物理问题.在弹簧缓慢腐蚀过程中，什么是浸渐不变量(或称为绝热不变量)? 本文求出这个问题的浸渐不变量，再将它推广到介观电容-电感回路的一种缓变情形，即讨论电解质电容中的电解液缓慢改变的情形下，什么是浸渐不变量.

1 弹簧缓慢腐蚀过程中的浸渐不变量

(1)

系统能量

腐蚀不但使得弹簧刚度k变小，也使得弹簧质量m变小，所以缓慢腐蚀引起的能量改变是

上式在平均意义下也成立.注意到平均势能与平均动能各占总能量的一半，所以有

鉴于

所以

积分得到

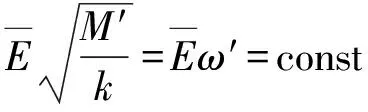
(2)

2 平行板电容器中的电解质液体缓慢腐蚀情形下的浸渐不变量

假设电路的电容是板面积为A的两平行板电容器，相距d，填满介电常数为ε的材料，那么电容是

每块板带电为Q，根据电磁学知识，电容器储能：

分开两块板所需的作用力作功：

所以一个板对另一块板的作用力F为

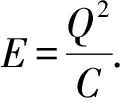
所以

积分得到

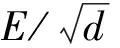
(3)

所以E/ω是相应的浸渐不变量.

上述电容电介质腐蚀的情况也可以推广到讨论磁介质磁导率的退化情形下的浸渐不变量，因情况类似，此处不详述.