函数零点虚设后的几种处理策略

魏东升

(江西省瑞金第一中学 342500)

函数与导数主要考查学生逻辑推理、直观想象和数学运算等核心素养的主要载体，其一直是高考考查的重点之一.在处理函数与导数的压轴题时，对零点的处理往往是一个关键环节，有些函数的零点确实存在，但无法精确求解，此谓之“隐零点”；有些导数的零点虽然可求，但因含参而需要讨论.对于这类问题，常见的处理方式主要有虚设零点和化隐为显两大类.

其中虚设零点是指为了处理函数的隐零点问题，通过采取假设函数零点却不直接求解，通过谋求整体的转化,将函数转化为易求的形式进行求解的一种处理技巧.本文通过结合2019年高考的几道导数压轴题，试图呈现隐零点问题中虚设零点后的几种策略，以供大家参考.

例1 (2019年江苏卷)设函数f(x)=(x-a)(x-b)(x-c),a,b,c∈R,f′(x)为f(x)的导函数.

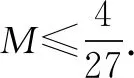
证法1 (降次留参)因为a=0,c=1，所以f(x)=x(x-b)(x-1)=x3-(b+1)x2+bx，

评析对于所求问题对应的高次函数含参，且其零点可求但形式繁琐，以致无法通过将该零点正常代入函数的方式求得最值时，可考虑对函数进行适当变形，以便零点可以以整体形式代入，从而达到降次以消去主元，只留下参数的方式.

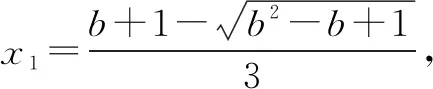
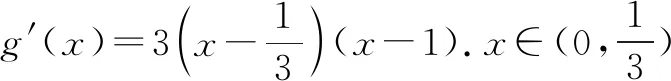
评析对于上述这种类型，除了降次留参的策略，还可以考虑通过参数的有界性消去参数，进而构造以零点为主元的参函数，通过放缩的形式间接达到要证明的结论.

例2 (2019年天津卷文)设函数f(x)=lnx-a(x-1)ex，其中a∈R.

评析如果所求问题对应的函数含参，但是参数可以通过所建立的方程关系比较方便地分离出来，则可考虑将该参数消去，只留下与所求问题有关的量.

(1)略；

(2)设x0是f(x)的一个零点，证明曲线y=lnx在点A(x0,lnx0)处的切线也是曲线y=ex的切线.

评析如果所求问题对应的函数是个超越函数(和指数函数、对数函数和三角函数等函数结合的函数)，在假设零点后，可以考虑把超越式(如lnx、ex等)分离出来再代入所求，以达到将超越函数转化为普通函数的目的.

例4 (2019年全国2卷文)已知函数f(x)=(x-1)lnx-x-1.证明：

(1)略；

(2)f(x)=0有且仅有两个实根，且两个实根互为倒数.

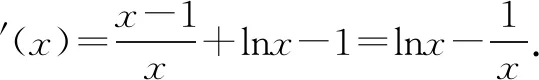
评析在一类函数零点个数判断(或根据零点个数求参、或零点所在区间判断)的问题中，往往会碰到判断导函数零点对应原函数值的符号，而零点本身并不可求，这时可以考虑利用该零点附近的特殊点的函数值来确定符号.

通过上述几个例题我们知道，结合已知条件和结论假设函数零点却不直接求解，通过谋求整体的转化,将函数转化为易求的形式进行求解的一类主要处理策略.在导数压轴题的教学过程中，像这样以专题的形式介绍隐零点问题的处理策略，尽量一次性彻底地解决与其有关的问题，对学生解题水平的提升、逻辑思维的训练和核心素养的培养，显然都是极好的.