三角形“五心”的坐标公式

甘志国

(北京丰台二中 100071)

三角形的重心坐标公式是大家熟知的(见以下定理1)，但笔者再解决有些问题时，还需知道三角形的外心、内心、垂心、旁心(它们和重心统称为三角形的“五心”)的坐标公式.比如，可以证明质线三角形(该三角形的质量均匀地分布在其三边上)的重心是其各中位线组成的三角形的内心.所以，本文给出三角形“五心”的坐标公式.

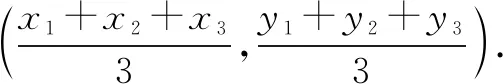
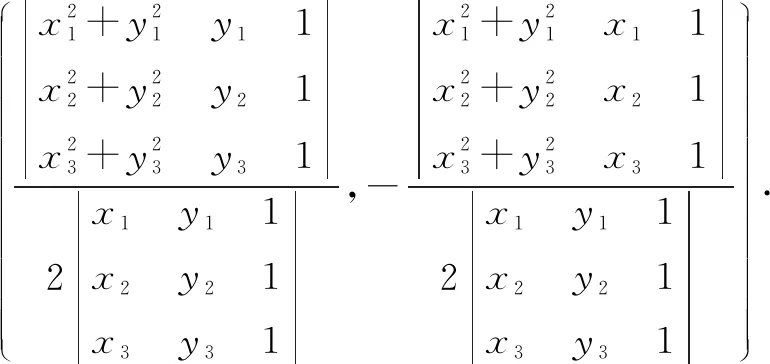
证法1可得边AB的中垂线方程是

(x-x1)2+(y-y1)2=(x-x2)2+(y-y2)2

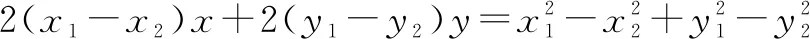
①

同理可得边AC的中垂线方程是

②

用行列式法解①②组成的二元一次方程组，得到的解就是△ABC外心Ω的坐标(因为任意三角形的外心存在且唯一，所以此方程组的解也存在且唯一)，通过解方程组可得：

从而可得欲证成立.

证法2可证△ABC外接圆的方程(可见盛祥耀，葛严麟，胡金得，张元德编《高等数学辅导(下册)》(1983年清华大学出版社)第17页第7.7题)

再用配方法可得欲证结论成立.

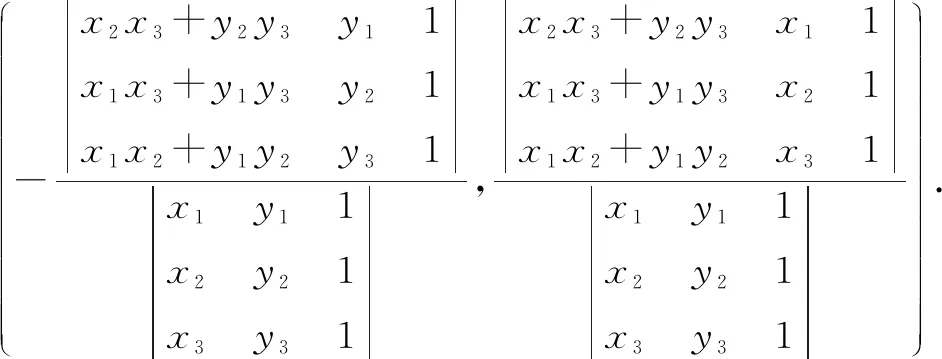
证明可得边AB上的高所在直线的方程是

(x1-x2)x+(y1-y2)y=(x1-x2)x3+(y1-y2)y3

③

(因为易知该直线与AB垂直，且过点C(x3,y3).)

同理可得边AC上的高所在直线的方程是

(x1-x3)x+(y1-y3)y=(x1-x3)x2+(y1-y3)y2

④

用行列式法解③④组成的二元一次方程组，得到的解就是△ABC垂心H的坐标(因为任意三角形的外心存在且唯一，所以此方程组的解也存在且唯一),通过解方程组可得：

([(x1-x2)x3+(y1-y2)y3](y1-y3)-[(x1-x3)x2+(y1-y3)y2](y1-y2)/[(x1-x2)(1-y3)-(x1-x3)(y1-y2)]，(x1-x2)[(x1-x3)x2+(y1-y3)y2]-(x1-x3)[(x1-x2)x3+(y1-y2)y3]/[(x1-x2)(y1-y3)-(x1-x3)(y1-y2)])

从而可得欲证结论成立.

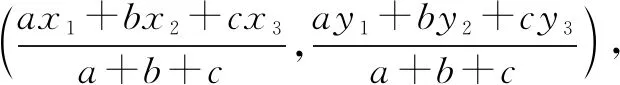
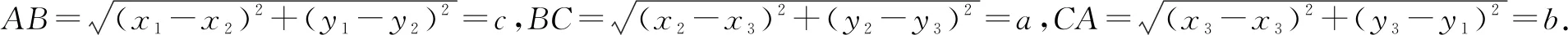
如图1，设AI交BC于D，连结BI,CI.

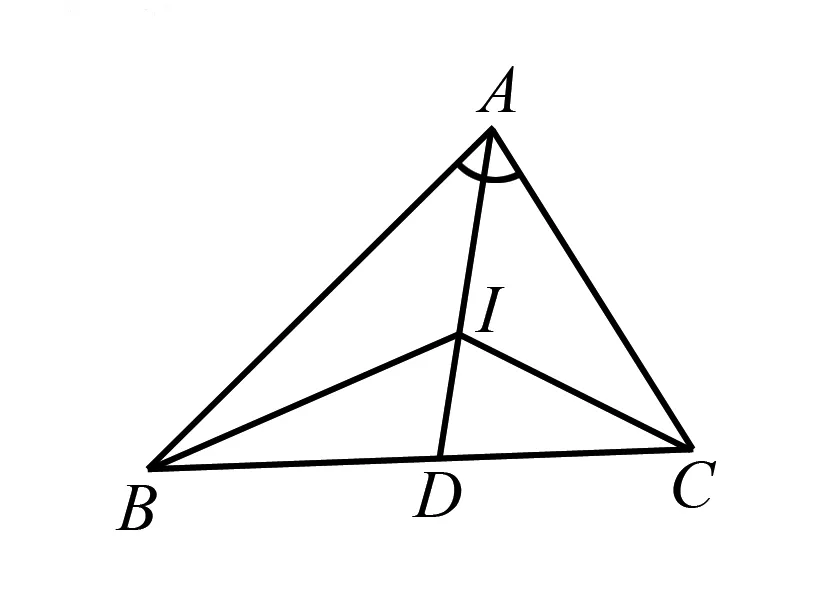
图1

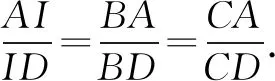
注贵刊发表的文献[1]也给出了定理4.

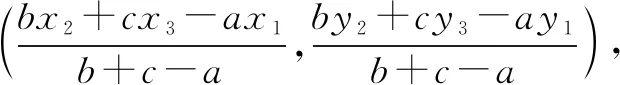
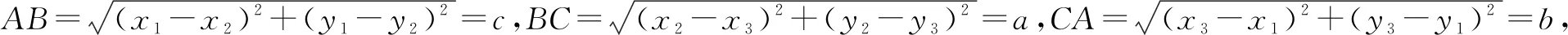
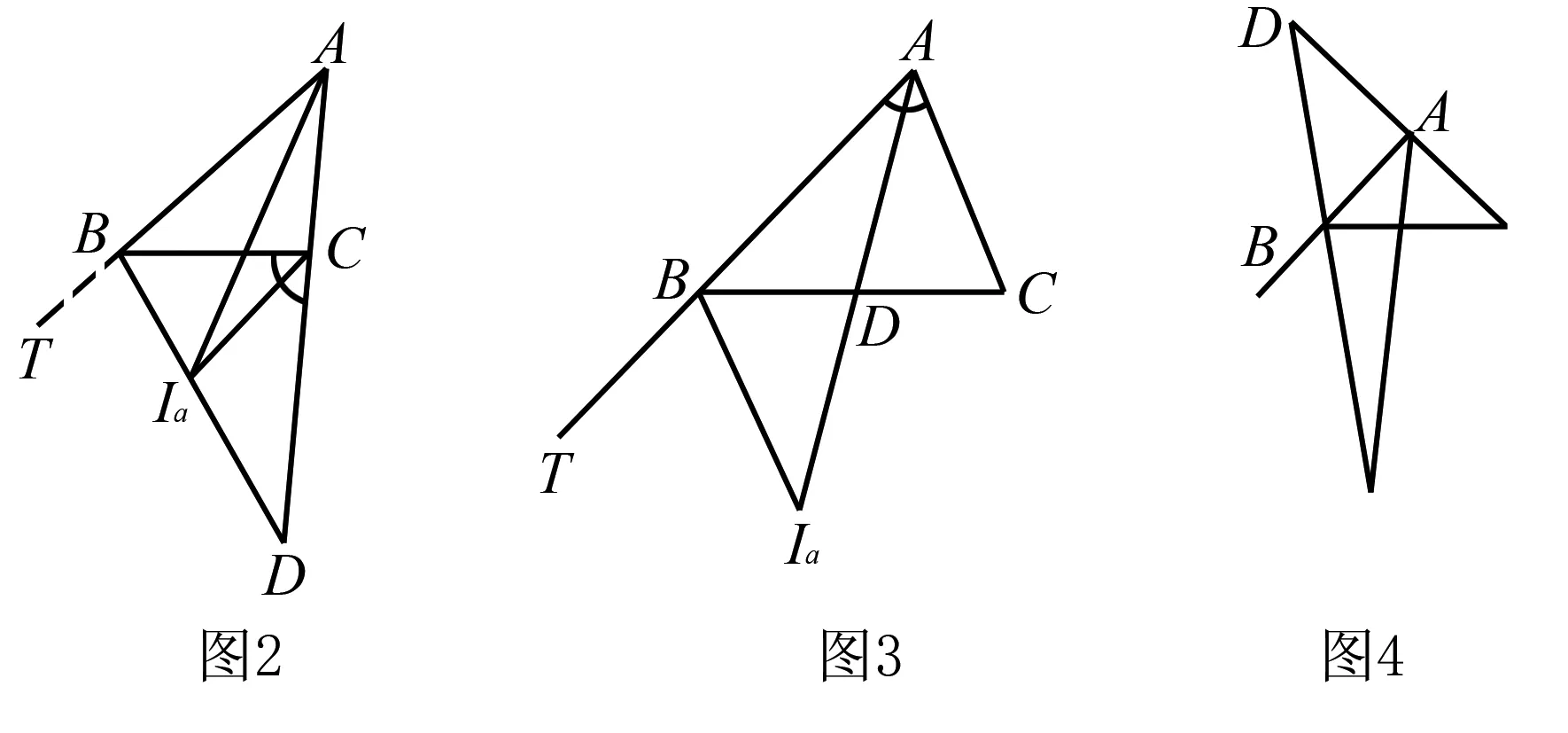
(1)当c>a时，如图2，可证△ABC的∠ABC外角的平分线与边AC的延长线一定相交(设交点为D)：即证∠CBD<∠ACB，也即2∠CBD<2∠ACB.

180°-∠ABC<2(180°-∠ABC-∠BAC),

2∠BAC<180°-∠ABC,

∠BAC<180°-∠ABC-∠BAC,

∠BAC<∠ACB,∴c>a.

所以欲证结论成立.