至少类问题的直接解答

俞新龙

(浙江省绍兴市柯桥区平水镇越崎中学 312050)

高中数学中有一种至少类问题广泛出现在各主干知识点中，此类问题常因直接解答时极易出错而且错误原因较难分析，从而通常以分类讨论形式解答，虽说问题也解决了，但实际上学生心里是不满意的，为什么不能使用首先在大脑中生成的直接解法来解答呢？本文对课本中一道例题的教学进行分析，试图对至少类问题的直接解答进行一次有益探索.

一、原题及解答

题目(人教版选修2-3第34-35页例8)在100件产品中，有98件合格品，2件次品，从这100件产品中任意抽出3件，

(1)有多少种不同的抽法？

(2)抽出的3件中恰好有1件次品的抽法有多少种？

(3)抽出的3件中至少有1件次品的抽法有多少种？

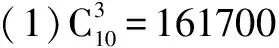
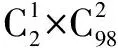
二、学生错误解法以及错误原因分析

绝大多数学生在解答上述第(3)小题时给出的并不是上述两种解法之一，而是下面错误的直接解答：

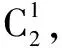
从答案上看显然是多算了，问题出在哪？到底多算了哪些？为了直观上理解这个问题，我们不妨采用列举法，又为了列举的方便且不会改变问题本质，我们不妨将问题改为：

在5件产品中，有3件合格品，2件次品， 从这5件产品中任意抽出3件，抽出的3件中至少有1件次品的抽法有多少种？

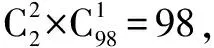
三、直接解答的进一步理解

为便于学生对正确的直接解答的理解，我们可以找下面的例子来帮助巩固.

1.通过集合来理解

在人教版的近几版教材中都有一份阅读与思考材料《集合中元素的个数》，该材料指出，对任意两个有限集合A，B，有card(A∪B)=card(A)+card(B)-card(A∩B)，所以对于选修2-3例8(3)来讲，我们可以从集合中元素的个数角度来理解.

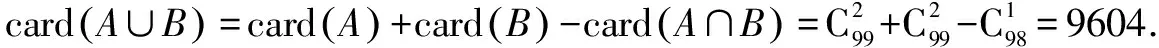
对于这个思路，还可以类比理解原例题的如下变式.

变式1 在100件产品中，有97件合格品，3件次品，从这100件产品中任意抽出3件，抽出的3件中至少有2件次品的抽法有多少种？

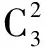
变式2 在100件产品中，有96件合格品，4件次品，从这100件产品中任意抽出3件，抽出的3件中至少有2件次品的抽法有多少种？

变式3 在100件产品中，有97件合格品，3件次品，从这100件产品中任意抽出3件，抽出的3件中至少有1件次品的抽法有多少种？

2.通过一道经典排列题来理解

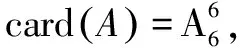
四、用直接解答解决问题

至少类问题存在于不同的主干知识中，为帮助学生对正确的直接解答方法的掌握，可通过类似以下习题的解答来强化.

问题1 已知关于x的二次方程x2+2mx+2m+1=0至少有一根在(1,+∞)内，求m的取值范围.

解析如果不是直接解答，一般常用分类讨论求解.

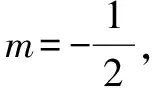
其实类似该题的问题完全可以直接解答：

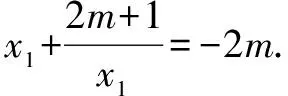
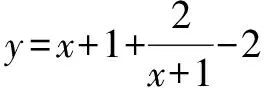
问题2 若方程2x2-ax+1=0在[3,+∞)上有解，求实数a的取值范围.

解析若不是直接解答，一般常用变量分离法求解.

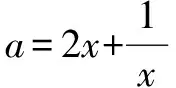
因为有解即表示至少存在一个，所以类似该题的问题完全可以直接解答：

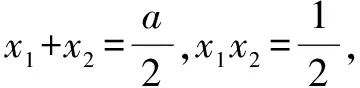
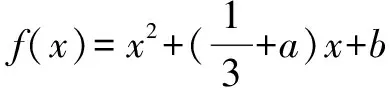
解析本题分类讨论求解非常繁杂，还是直接解答来得比较好.

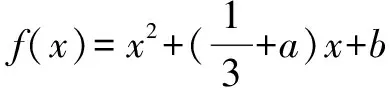
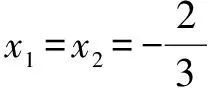
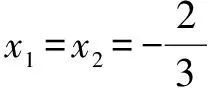
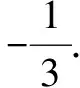
五、一点想法

哈尔斯说：“问题是数学的心脏.”数学学习离不开解题，波利亚说：“中学数学的首要任务就是加强解题训练”“解题是一种实践性的技能，就像游泳、滑雪或弹钢琴一样，只能通过模仿、练习和钻研来学到它.”因此，在解题教学实践中，教师讲解时应该找准解题教学的着力点，笔者认为像本文前面论述的这种情况正是教师应该着力研究并解决的解题状况，也符合在学生最近发展区开展教学的要求.最后以美国著名数学教育家波利亚说的一句话与老师们共勉：“一个专心的认真备课的教师能够拿出一个有意义的但又不复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域.”