变式训练教学模式在初中数学解题中的应用探索

官月兰

(福建省光泽第二中学 354100)

数学能力是初中阶段的基本能力之一，而数学学科的基本作用是在有限的课时内，通过数学题目的展示和分析，使学生充分感受理性分析的魅力，扩展思维广度，加强对实际生活的感知程度，进而深入落实创新精神的培养办法.变式训练教学模式能够很好的对接初中数学的基本作用和要求，结合学生的发展脉络，适当提升运用比例，帮助学生构建数学模型，形成全面的知识结构.

一、变式训练的基本内涵

从字面意思理解，通过转变思维和思考方向，将原有题目转变解决的办法和形式，形成最优解的过程.从数学内涵上看，通过合理规划数学题目，找到题目中隐含的本质性问题，结合不同学生的发展进程，运用不同的思维深度和层面，对接题目本质性问题，最终应用到现实题目中，形成完备的解题办法.因此，变式训练教学模式是一种有助于提升学生思考、分析和运用能力的方法，对于提升学生知识水平的深度有着积极的促进作用.

二、变式训练的基本原则

变式训练教学模式有以下几种原则：

1.指向性

指向性原则指的是基于数学知识多变性的特点，利用数学规律和逻辑分析开展变式训练的过程中，教师需要顺应学生的发展特点，结合其掌握数学知识的水平，并且立足于教材内容，开展有针对性的教学活动，从而使训练过程有很强的指向性.

2.适度性

适度性与针对性在本质上是相似的，适度性是指教师在引导学生转变思考方向的进程中，不应凌驾在学生现阶段情况之上，要明确他们能够接受的知识水平，适度提升问题思考的难度，引导他们以最近发展区的水平，分析已知问题.适度性的原则要求教师在教学中，不能只考虑应用数学知识的难度，还应当了解是否因为题目的变化，为学生的思考增加不必要的负担.

3.集中性

集中性体现在教师选用的方法，学生应当参与进来，充分满足他们对于数学学习的欲望，提升自主探究的兴趣.教师要设置生活情境，创建和谐的课堂气氛，为学生构建一个能够充分展示自我的平台，使他们感受到作为学习主体的意义，加强对知识的探究.

三、变式训练教学模式在数学解题中的应用

1.以教材为基础，多层面迁移

变式训练将教材内容作为变化的前提条件，立足于教材中对学生知识和能力水平的要求，挑选典型例题，通过更改题目基本条件，充分调动学生的思考深度，提取有关数学记忆，完成题目的分析解答过程.对于初中数学来说，教师在明确基本数学概念和运算定理后，在一道题中使用不同的方法，使学生了解一题多解的办法，从而扩展思维广度.

如图1所示的题目类型，可以首先分析图形结构，发现这是一个不规则的图形，看起来像是三个三角形堆叠到一起，形成的交差结构.

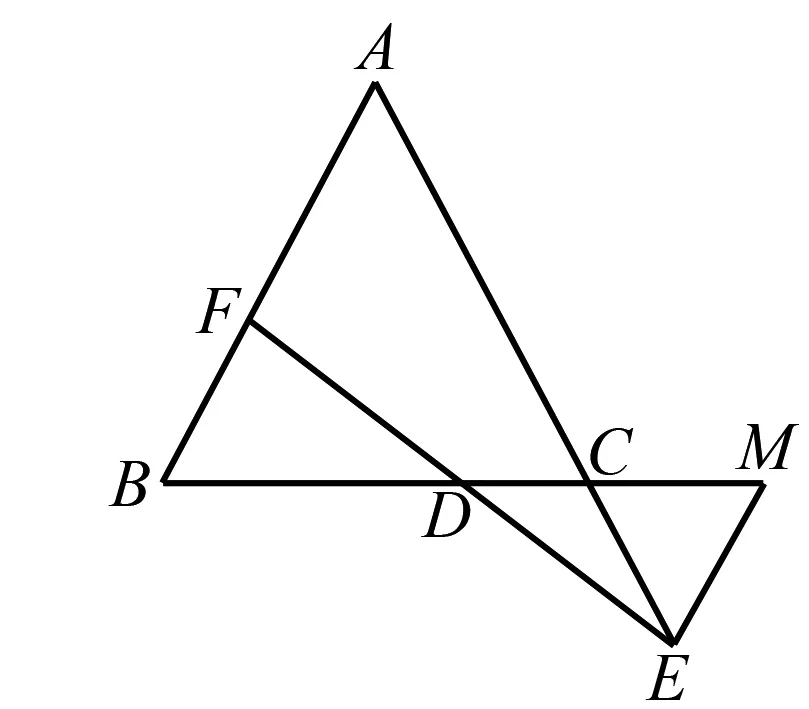
图1

如图1，已知AB=AC，E是AC延长线上一点，且有BF=CE，连接EF交BC于D.求证：FD=DE.

面对此种结构的解决办法是从题目本身出发，利用全等三角形的判定定理、平行四边形的判定定理、中位线的性质等，选用不同的思考方向，解决该问题，下面提供几种对应的解答方式，供大家参考：

(1)作图如图2所示，此时BF=GC，∵AB=AC且BF=CE，∴GC=CE，根据中位线性质，最终判定出FD=DE.

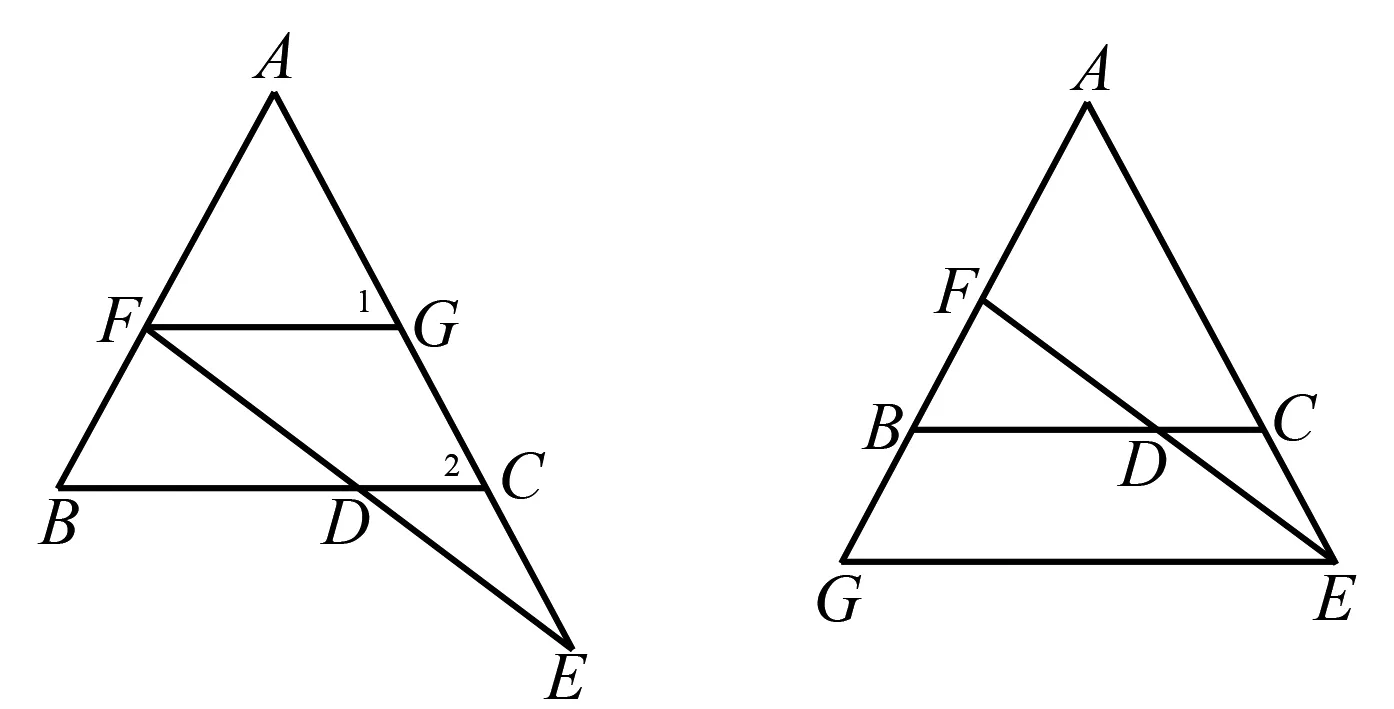
图2 图3

(2)作图如图3所示，取一点G，使CE=GB，则GB=FB，根据BA=AC得到BD∥GE，根据中位线性质，得到FD=DE.

以上给出的两种方法是基础的解答形式，学生可以根据小组探究和自我研究的方式，调取之前所学的内容，满足学生思维发散的要求.教师在学生小组探究中应当起到引导的作用，多方面考量他们的基本知识结构，找到提升学生学习兴趣的方法.

2.构建数学模型，统一内在联系

有些数学题目间存在内在联系，虽然题目要求和解决问题的方式不同，但究其根本使用的是统一的数学知识理论，对于此类问题，教师要及时记录，通过收集和整理此类数学问题，找到其中隐含的数学知识.课堂上，通过深度展示数学题目，使学生感受到知识间的联系，结合比对解题办法，得到内在联系的证据，从而构建数学模型.这种归化同类问题的方式，能够有效形成处理和解决数学问题的能力.例如，教师为了使学生深刻了解毕达哥斯拉定理的内容，希望他们可以结合自我探究的过程，对数学定理有深刻的认识.在课堂中，利用多媒体动画为学生展示，在直角三角形中，分别以每条边为边长做正方形，然后布置思考任务，让学生根据图形的演示结果，找到三个正方形面积之间的关系.此类属于基本性问题，学生仅通过运用勾股定理和正方形面积计算公式，就能够得到最终面积关系.教师先不急于为学生提供定理的主要内容，而是继续为他们播放以直角三角形三条边为边长和半径的等边三角形和半圆，允许其以小组讨论的方式，计算出面积关系.结合图形的变换，学生逐渐深入到定理内部，将不同形式的问题和已知条件整合成一种思想，最终形成数学模型.

3.运用发散思维，提升数学能力

变式训练教学模式完美的契合发散思维训练的要求，学生在处理同一道问题的过程中，选用不同的数学理论作为解题的基础，结合具体过程比对出不同方法的优缺点以及运用的基本定理，不仅锻炼了他们整合和应用知识的能力，还充分扩展了他们的思维广度，提升创新思维的运用深度.例如，教师在解决图形问题中，选用不同的图形验证方式，靠近最终求证的内容，帮助学生理顺每个求证方法的具体适用原则，提升对基本理论的应用广度.

4.提升变式训练教学模式效果的方法

(1)培养学习兴趣

学生的兴趣是转变教学方式的基准点，变式训练教学模式对于基础较差的学生来说，如果教师选用的刺激兴趣的方法不当，容易给学生造成思想的负担，使他们产生畏难情绪，从而不愿意深入到探究中去.由此可见，教师要适当结合多媒体、微课等新型教学模式，渗透多种教学方法，达到全面提升学生参与度的效果.

(2)扩展学生思维

教学中适当增加拓展思维的题目，无需选用难度较大的题目，容易使学生失去处理数学问题的自信，不利于发展数学思维.因此，教师在选择题目的过程中，注意结合学生知识的掌握情况，有针对性的设置问题和变化形式，加强他们对数学理性的认知.

(3)教学详略得当

教学中注意主次分明，对于不适合和没必要使用变式训练的内容尽量不要占用太多的教学时间，这会增加学生的负担，尤其是对于初三复习的学生，大量没有章法的数学题只会给学生营造一种数学题目繁多复杂的气氛，不利于变式训练的开展和能力的提升.

综上所述，在初中数学中加强变式训练，需要选用具有指向性特定的训练方式对接不同学生的发展特点，找到最优解，加强对知识的理解深度.不难发现，变式训练是一种创新性的数学教学行为，通过整合多种数学知识要点，寻找统一的思考渠道，将学生带离原有数学意识的框架，跳出固有思维的心智，充分应用他们的理解和实践能力，把一道数学题变为多种能力提升的工具，发展学生思维，加强数学知识的应用效果.