“线性相关”教学案例及分析

曾振新

(云南省西双版纳职业技术学院 666100)

美国学者萨普认为，“概念在数学中不仅是首要的，而且实际上就是一切；在很大程度上，‘数学对象’没有独立的或超过概念之外的存在”.《线性代数》课程中，有许多概念需要认真学习和领会，特别是在线性空间的知识内容中碰到的概念会更多一些.

一、关于线性相关概念的分析案例

线性空间的基本元素是向量，向量之间的第一层关系是“线性组合”或者称“线性表示”.然而，与之密切相关的“线性相关性”在《线性代数》整个课程中却占有很重要的位置.

《线性代数》教材中关于“线性相关”的定义是这样表述的：对于向量组α1，α2，…，αs，如果存在不全为零的数k1,k2,…,ks使关系式k1α1+k2α2+…+ksαs=0成立，则称向量(组)α1，α2，…，αs线性相关；否则称向量(组)α1，α2，…，αs线性无关.满足上面等式的不全为零的数k1,k2,…,ks，称为向量组α1，α2，…，αs的一组相关系数.

1.教学分析

一个数学概念的给出，总要回答这样两个问题，一是为什么，即有什么作用.二是怎么做，即如何解决这样的问题.

本定义提供的重要信息是它是用来判别一组向量是否是线性相关或线性无关的，即它的作用.很明显，在定义中，给出了基本条件有两个，即：

(1)有s个向量α1，α2，…，αs；

(2)s个实数k1,k2,…,ks.

显然，定义中，也给出了两个判断条件即：

(1)满足一个线性关系即：k1α1+k2α2+…+ksαs=0；

(2)s个不全为零的数或s个全为零的数.

本定义提供的第二个信息是如何来判断一组向量是线性相关或线性无关.因为判断条件是一个等式及这个等式中的这s个数即k1,k2,…,ks，因此，解决问题的关键因素是求出k1,k2,…,ks这s个数，即解齐次方程.

2.问题解决分析

对任意向量组α1，α2，…，αs，总有0α1+0α2+…+0αs=0，问题是是否存在不全为0的数k1,k2,…,ks，使得关系式或方程k1α1+k2α2+…+ksαs=0成立，若存在，则α1，α2，…，αs线性相关；若不存在，则α1，α2，…，αs线性无关(不存在的意思是k1α1+k2α2+…+ksαs=0充分必要条件是k1=k2=…=ks=0).

此问题的关键点是求关于未知数x1,x2,…,xs的线性方程x1α1+x2α2+…+xsαs=0的解，有非零解，即α1，α2，…，αs线性相关；若仅有零解，则α1，α2，…，αs线性无关.

3.逻辑关系分析

我们知道，数学课程的设置总是以演绎严谨的思维、表现慎密的逻辑关系，来达到培养人的心智功能，并鼓励人们求真、向善、唯美为目的的学科.所以数学学习的过程就是一段逻辑演绎的过程，《线性代数》也不例外.

显然，无论是解齐次线性方程组还是一般线性方程组，都需要矩阵的知识，即矩阵的初等变换，重点是矩阵的秩.求矩阵的秩还需要行列式的知识，环环相扣，缺一不可.

而线性相关概念后的知识走向，就是求极大线性无关组，得出线性方程的基础解系，从而获得线性方程的全部解.还可得到线性空间的基，线性空间的维数及任意线性空间向量的坐标，这是其中一个落脚点.

综上所述，认识、理解和解决数学概念问题的基本方法应该是：了解概念的过去，然后再思考它的未来.

二、相关问题解决案例分析

1.例题评析

例设空间任意向量α,β,γ，证明：α+β，β+γ，γ-α线性相关.

方法一常规的解法是应用定义，即先求解线性方程组：x1(α+β)+x2(β+γ)+x3(γ-α)=0的解，然后再来判断.

证明：可以设有一组数k1,k2,k3使k1(α+β)+k2(β+γ)+k3(γ-α)=0成立，整理得

(k1-k3)α+(k1+k2)β+(k2+k3)γ=0.

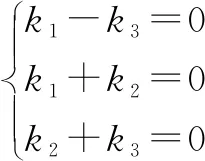
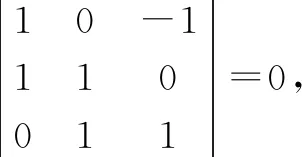
本法证明中规中矩，逻辑平稳、严密，体现出了数学思维(演绎推理的思想方法)的普遍现象，是一种常用的解题方式.

然而，解题中也有少数学生给出了如下证明，

方法二证：∵α+β=(β+γ)-(γ-α)

∴α+β，β+γ，γ-α线性相关.

方法三证：由∵(α+β)+(β+γ)+(γ-α)=2(β+γ)得(β+γ)=(α+β)+(γ-α),∴α+β，β+γ，γ-α线性相关.

能给出方法一、方法二这样的证明，需要有一定的联想能力，即应用相关的定理：“向量组线性相关的一个充要条件是向量组中有一个向量是其余向量的线性组合”来证明该结论.而在文中的《线性代数》教材中没有例出该定理的情况下，有学生能够考虑到这种简明的方法，干净利落，很出乎意料.

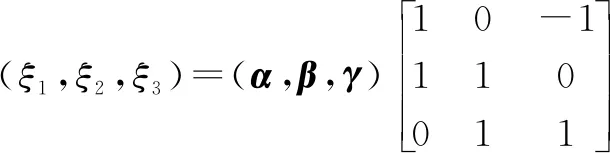
从而ξ1=α+β，ξ2=β+γ，ξ3=γ-α线性相关.

问题思考：如果上题条件改变为设空间向量α,β,γ线性相关，证明：α+β,β+γ,γ-α线性相关.事实上，这可以把它看作是原例题的特例.

当然，相对于一部分人来说，这么反复折腾一个概念也没有什么实际意义.在柏拉图主义看来，数学的研究和学习并不是为了要有实用价值，而是为了最高形式的理性训练，对绝对理念的感悟和认识，以及对哲学研究有益.

2.线性相关性的几何解析

基本概念:①两向量共线的充要条件是它们线性相关.

②三向量共面的充要条件是它们线性相关或混合积为0.

③空间的任意四个或以上的向量总是线性相关.

方法五仅证明混合积为0.即：

(α+β,β+γ,γ-α)=0

∵[(α+β)×(β+γ)](γ-α)

=[α×β+α×γ+β×β+β×γ](γ-α)

=(α×β)γ+(α×γ)γ-(β×γ)α

=0

或∵(α+β)×β=α×β

(β+γ)×β=-γ×β

(γ-α)×β=γ×β-α×β

∵[(α+β)+(β+γ)+(γ-α)]×β=0

∴α+β,β+γ,γ-α向量共面即线性相关.

方法六设α,β,γ是三维空间的任意向量，并令

α=(x1,y1,z1),β=(x2,y2，z2),γ=(x3,y3,z3)

则有(α+β,β+γ,γ-α)

所以三向量α+β,β+γ,γ-α线性相关.

可以看出，线性代数与空间解析几何也有密切的联系，本来《线性代数》研究的主要内容就是向量.而几何的基本元素是点、线、面相对应也是向量.因此，在讨论线性空间的概念时，用几何的方法来思考也是学习者常常用到的.

三、问题推广及一题多解案例

例1设向量α1,α2,…,αn线性无关，证明：向量组β1=α1，β2=α1+α2，…，βn=α1+α2+…+αn也线性无关.

证明 方法一由于向量组α1,α2,…,αn线性无关，则可作为n维空间的一组基，从而向量β1=(1,0,0，…，0)，β2=(1,1,0，…，0)，β3=(1,1,1，…，0)，……，βn=(1,1,1,…,1),由行列式知

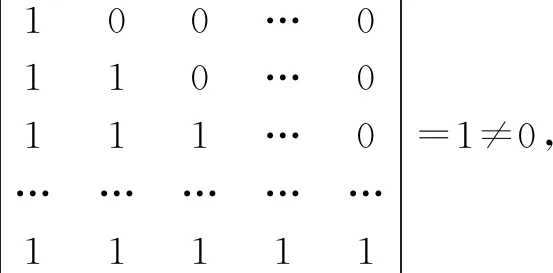
推广应用：对于向量

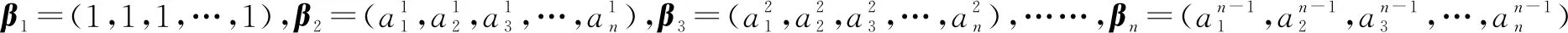
方法二按定义设存在k1,k2,…,kn∈R,使k1β1+k2β2+…+knβn=0.从而有

k1α1+k2(α1+α2)+…+kn(α1+α2+…+αn)=0

(k1+k2+…+kn)α1+(k2+k3+…+kn)α2+…+knαn=0,而α1,α2,…,αn线性无关，即有k1+k2+…+kn=k2+k3+…+kn=…=kn=0,所以,k1=k2=…=kn=0即向量组β1，β2，…，βn线性无关.

例2 求向量组α1=(2,4,2)，α2=(1,1,0)，α3=(2,3,1)，α4=(3,5,2)的一个极大无关组，并把其余的向量用该极大无关组线性表示.

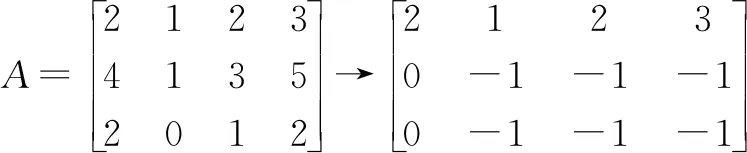
解方法一 常规解题，由3维向量组α1，α2，α3，α4得到对应矩阵并实施初等行变换：A=

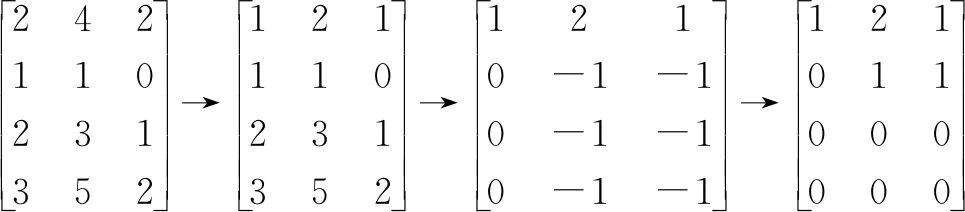
得矩阵的秩为2，且极大无关组为α1，α2.

再由方程x1α1+x2α2=α3和方程x1α1+x2α2=α4分别得到两个方程组：

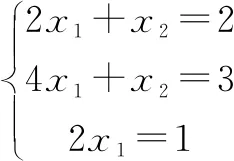
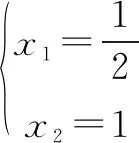
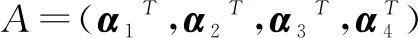
由最后一个矩阵可知：α1，α2为一个极大无关组，从最后一个矩阵直接得知：

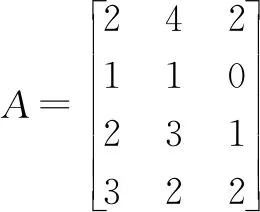
对A施以初等行变换，化为阶梯形矩阵，并在矩阵右侧标注所作的变换：

由最后的阶梯形矩阵可知，α1，α2为一个极大无关组，通过对每一步的计算纪录得到：

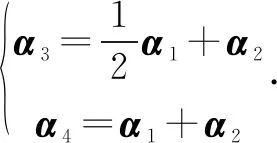
事实上，本题是一道典型的关于线性相关性的例题，即是对线性相关性概念学习的一个小结，也是这一章节学习的主要目标.

四、问题和展望

现在很多学生也包括相当一部分教师流行数学学习的“无用论”，但从以上的理解和解题中，我们分明看到了智慧的光芒.实际上，数学以严谨的逻辑思维为手段的学习方式能够充分发挥人的心智功能，从而使数学具备了除了应用价值以外的理性价值.

近一两百年间，全世界的专业学院在各自的领域内做出的最大贡献，可能不在于培养多少实用型的工程师、律师或医生，而在于开展了大量看似无用的科学活动.某种程度上，数学活动就是这样的一种科学活动.从这些无用的科学活动中，我们获得许多发现，它们对人类思想和人类精神意义之重大，远远胜过这些学院建立之初力图达成的实用成就.

数学教与学原则从来都是让学生了解数学知识“从何而来，到何处去”.如果我们遵循这一原则，那么，我们就会站得更高，看得更远，想得更透.