核心素养视野下的高中函数恒(能)成立问题教学“再创造”

马宝星

(江苏省沙溪高级中学 215400)

高中函数恒(能)成立问题是高考的热点，也是学生学习中的难点，贯穿高中三年数学学习，如何在高三二轮复习中突破难点，提升能力，是每个老师都积极努力的目标.但是高中数学学科因其特殊性，很多高三数学课堂存在一定的困难，包括教师层面重复讲解，学生方面重复训练，最后师生深陷题海，并没有实现数学学科的核心素养这个目标.整体的效率低下，教师和学生都苦不堪言.可见习题教学在高三数学学习的重要性，进行合理的数学学科的教学设计，在实现数学核心素养的目标上往往能起到事半功倍的作用.笔者以一节高三二轮复习课为例阐述如下：

一、“再创造”的教学设计重视辨析概念的内涵和外延，把握数学本质

问题一：什么是恒(能)成立问题？

设计意图：章建跃老师曾说：数学教学的基本任务是帮助学生将数学知识理解到位，并能用于解决实际的问题.我们要讲清楚一类问题，就必须要引导学生弄清其本质，才可以做到更好的去应用.恒成立问题，是高中数学中的全称命题，通常含有“所有的”“任意一个”等全称量词，符号语言可记为∀x∈M,P(x).能成立问题，是高中数学中的存在命题，通常含有“存在一个”“至少有一个”等存在量词，符号语言可记为∃x∈M,P(x).并且全称命题∀x∈M,P(x)的否定为：∃x∈M,P(x)，存在命题∃x∈M,P(x)的否定为：∀x∈M,P(x)，这里我们可以看出两类问题是可以相互转化的，类比恒(能)成立问题，其实高中数学中很多核心概念如单调性、奇偶性、周期性等都含有“任意”字眼，具有相似的处理策略.笔者认为，尽管二轮复习时间紧任务重，但我们不能就题论题，应引导学生深刻领会常用逻辑用语在数学问题中的作用，才能提升数学的问题解决.

二、“再创造”的教学设计重视问题情景的开放性，提高探索能力

例题精讲已知函数f(x)=lnx-ax，g(x)=x2,a∈R.若f(x)≤g(x)恒成立，求a的取值范围．

问题二：如何求a的取值范围？

问题三：你们还有没有其他做法？大家思考3分钟.

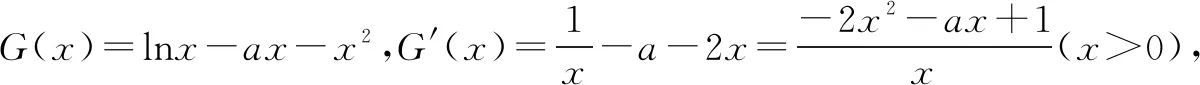
生3：令F(x)=lnx-ax-x2≤0对∀x∈(0,+∞)恒成立，所以F(1)=-a-1≤0,得a≥-1，所以F(x)=lnx-ax-x2≤lnx+x-x2，易证lnx≤x-1,当且仅当x=1时取“=”，故F(x)≤x-1+x-x2=-(x-1)2≤0，所以a≥-1成立.(教室里出现了掌声)

问题四：如果本题是填空题，如何求a的取值范围？

生4：由题知，ax≥lnx-x2，y=ax与y=lnx-x2皆好作图，如下图易得a的取值范围.

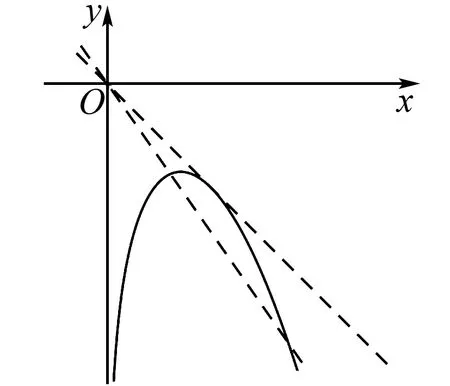
图1

点评生1选择了参变分离法，由于分离变量后h(x)的最值好求，故大部分同学皆选此法；生2选择利用函数的性质，通过求导，求G(x)=lnx-ax-x2的最值，只要G(x)max≤0，这个过程中导数的零点存在，直接求出比较繁琐，他采用了“隐零点”的处理方法，求出x0的取值范围，根据x0与a的等量关系求出a的取值范围；生3抓住了F(x)=lnx-ax-x2≤0对∀x∈(0,+∞)恒成立这一本质，它一定对x=1时恒成立，故F(1)≤0，求出a的取值范围，这一必要条件开路的技巧，体现了由一般到特殊的性质，数学问题解决的特殊化可使学生的直观想象素养得以提升；生4是把恒成立问题转化为两个图像的位置关系问题，体现了数形结合思想.笔者认为，在二轮复习教学中，学生已经有了一定基础，我们可以设计开放性问题，大胆放手让学生解决，激励学生更好地参与问题，提出不同见解，在多种方法甚至犯错中加深问题理解，优化解题方法，提高复习效率.

三、“再创造”的教学设计重视学生的自主总结，形成知识体系

回顾高考(2020山东)已知函数f(x)=aex-1-lnx+lna．若f(x)≥1，求a的取值范围．

本题的解题方法有多种，其中有的同学说还可以构造同构处理：f(x)=aex-1-lnx+lna=elna+x-1-lnx+lna≥1等价于elna+x-1+lna+x-1≥lnx+x=elnx+lnx,

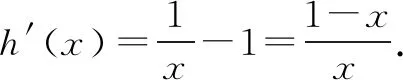
在(0,1)上h′(x)>0,h(x)单调递增；在(1,+∞)上h′(x)<0，h(x)单调递减，

∴h(x)max=h(1)=0,lna≥0，即a≥1，∴a的取值范围是[1,+∞).

问题五：本节课我们学习了恒(能)成立问题的哪些解决方法？

设计意图：《普通高中数学课程标准(2017年版)》指出：通过高中数学课程的学习，学生能养成良好的数学学习习惯，发展自主学习的能力.一节高三复习课，作为教师，到底要教会学生什么，通过知识载体能够提升学生哪些数学素养，是我们每一节课前需要仔细思考的问题.笔者认为，让学生“动起来”，“动”“静”结合，有条不紊，才可以不断提高学生的实践能力.本节课留足时间让学生自主总结，可以采用点名提问、小组讨论、师生生生互动点评等方式，增强学生的自主性.引导学生在实践解决问题中，能够自主构建知识网络，绘制数学思维导图如下.在同伴、老师不断提醒中，回顾旧知识，唤起新知识，在同伴老师的赞赏中增强学好数学的自信心，夯实自己的薄弱，强化各自的学习能力，才可以在以后再碰到类似问题，无间断的迁移到本节课所学知识方法，用好用活恒(能)成立问题的解决策略.

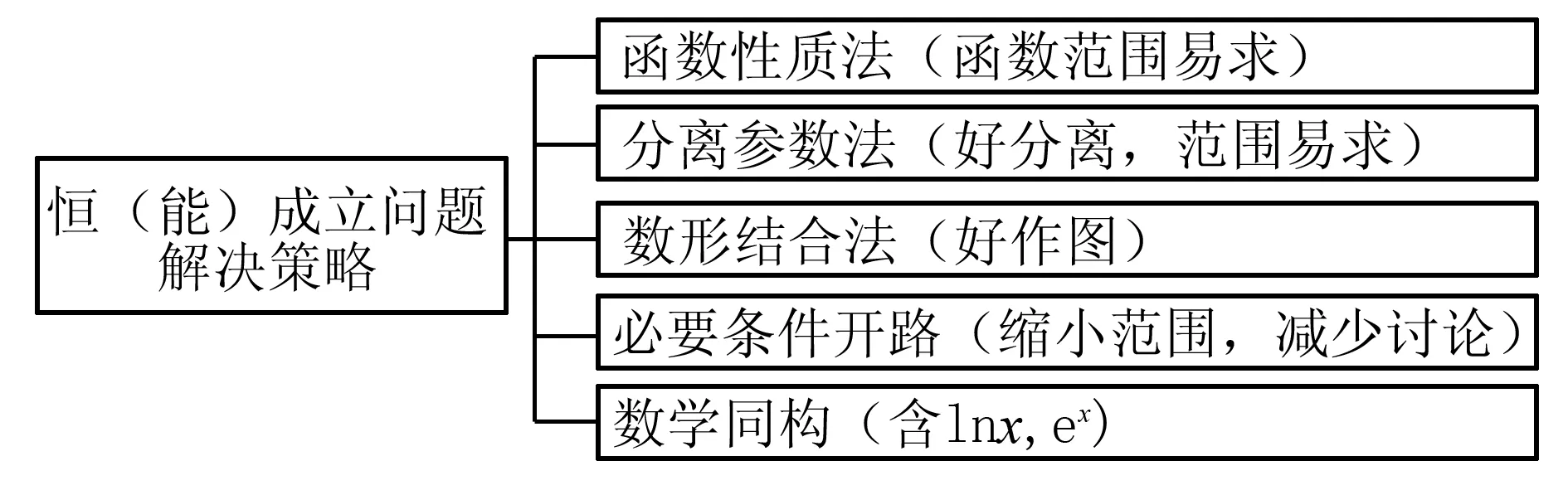
图2

本节课从一个典型例题出发，通过一般化的概念理解，特殊化、类比、联想等思维活动提出新的数学问题和变式，师生探究，学生总结形成解决问题的一般策略，注重数学思想、逻辑连贯、系统总结，用“数学的方式”教数学学数学.通过“创造性”的教学设计，强化“四基”，提高“四能”，超越数学知识而使数学核心素养真正落地.