基于单方向阻尼源项的数值消波方法

王凡瑜，权晓波，魏海鹏，孔德才

（北京宇航系统工程研究所，北京 100076）

波浪是水利工程、船舶与海洋工程等领域关心的重要环境因素之一。研究波浪及其影响主要有实验与数值模拟两种手段。数值模拟手段具有成本低、可研究的空间尺度大等优点，并能够较简便地模拟更接近真实水文环境的各种不规则波，在工程实践中发挥着重要作用。

数值消波方法用于消除计算域出口附近产生的反射波，避免反射波影响上游流场，是开展波浪数值模拟的关键点之一。其中人工阻尼消波法通过修改控制方程模拟自然界中沙滩或实验水槽中消波端的阻尼作用实现消波，具有实现简便、适用于非线性波数值模拟的优点，在波浪数值模拟中得到了广泛应用。ISRAELI M等[1]首先提出人工阻尼消波法，其后LARSEN J等[2]以及BAKER G R等[3]分别在Boussinesq方程和二维边界元模型中实现了人工阻尼消波。国内方面，高学平等[4]结合人工阻尼消波法和辐射边界条件消波法模拟了二阶Stokes波、驻波与不规则波，董志等[5]基于人工阻尼消波法比较了不同造波方法的二阶Stokes波模拟效果，査晶晶[6]在开源计算流体力学软件OpenFOAM中植入了人工阻尼消波法，王巧莎等[7]研究了适用于不同重力加速度条件与不同波陡条件的人工阻尼消波法，穆泽楠[8]基于人工阻尼消波法比较了不同造波方法的不规则波模拟效果。但是一些研究[6,9-10]指出，波浪数值模拟中存在如图1所示的平均自由面缓慢抬升现象，数值解波形逐渐向上偏离解析解，使波浪模拟精度略有损失，给开展波浪数值模拟带来一定困扰。

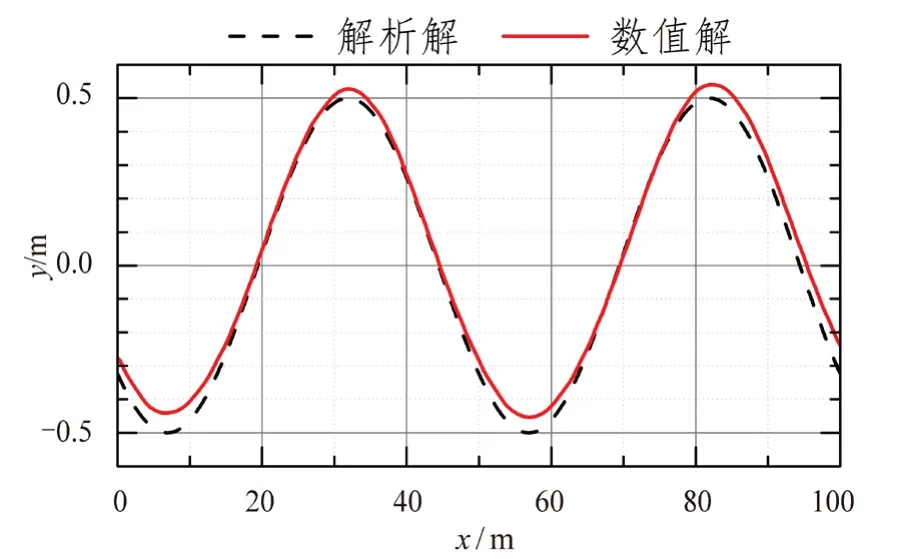
图1 平均自由面抬升现象

本文提出了一种基于单方向阻尼源项的数值消波方法，采用VOF模型与边界条件造波法模拟了大、小两种波陡条件的线性波，通过比较获得的数值波面并定量分析平均自由面抬升程度，验证了单方向阻尼源项抑制平均自由面抬升的效果。在此基础上，进一步研究了阻尼系数与密度依赖性对波浪数值模拟精度的影响。

1 数值方法

1.1 控制方程

对常黏性系数牛顿流体的二维不可压缩流动，有连续性方程：

动量方程：

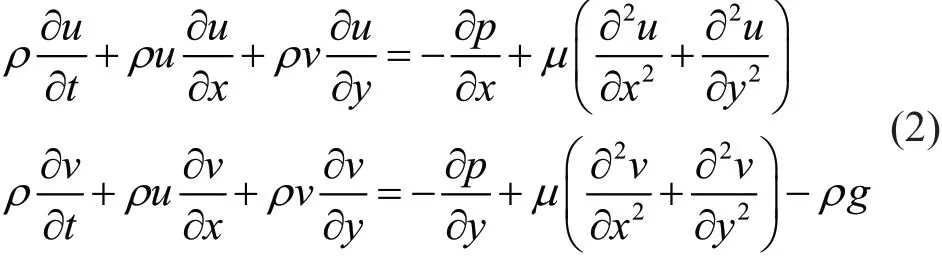
式中：u、v分别为水平速度分量与竖直速度分量；ρ为密度；p为压强；μ为动力黏性系数；g为重力加速度。

气水自由面采用VOF模型[11]模拟，相分数隐式求解；瞬态项采用一阶隐式格式离散，压力项采用PRESTO!格式离散，对流项采用二阶迎风格式离散；控制方程组采用SIMPLE算法[12]求解。

1.2 造波方法

本文采用边界条件法造波。边界条件造波法根据波浪解析解或数值解设置入口边界的速度条件与相分数条件，具有计算量小、易生成各种波浪的优点。

以线性波为例，波浪理论指出，自由面高度为：

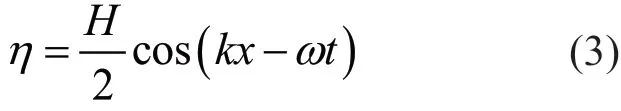
液相速度分量为：

式中：H为波高；k为波数；ω为角频率；T为周期；d为静水水深。入口边界的相分数条件可由式(3)确定，速度条件可由式(4)确定。

1.3 消波方法

1.3.1 人工阻尼消波法 人工阻尼消波法以多孔介质模拟自然界中的沙滩或实验水槽中的消波端。假设消波区填充有多孔介质，为模拟对流体运动的阻碍作用，向式(2)右端添加阻尼源项。

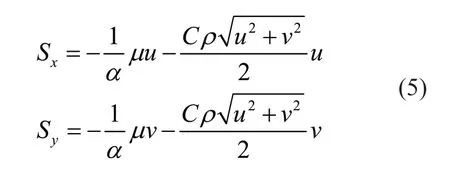
式中：μu/α和μv/α反映多孔介质导致的黏性损失，α为多孔介质渗透率；和反映多孔介质导致的惯性损失，C为惯性阻力系数。实际使用中一般只取μu/α和μv/α，并改写为[6,8,13]：

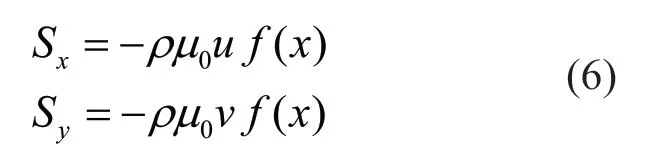
式中：μ0为阻尼系数；f(x)为阻尼分布函数。通常采用线性阻尼分布函数：

使阻尼源项自消波区起始端从零逐渐增大，以避免在消波区起始端产生反射波。式中xs、xe分别为消波区起止端水平坐标。

1.3.2 单方向阻尼源项 多孔介质对流体运动的阻尼作用使消波区内流体趋于静止，在避免出口处产生反射波的同时，也阻碍流体通过出口边界流出。采用边界条件造波法时，液相流体在入口边界存在净流入量，计算域内液相流体总量不断增加，使得平均自由面高度不断抬升[6]。

平均自由面抬升的根本原因是计算域内液相流体总量不断增加，故考虑取消水平方向阻尼，即令

以减少流体水平速度衰减，使液相流体能够通过出口边界流出，降低计算域内液相流体净增量。为尽可能避免出口处产生反射波影响上游流场，仍保留竖直方向阻尼，使自由面波动在消波区内逐渐衰减。因仅有竖直方向阻尼源项，所以称作基于单方向阻尼源项的数值消波方法，相应地将式(6)所示的阻尼源项称作两方向阻尼源项。1.3.3 密度依赖性 一些研究[5,7]采用常系数代替阻尼源项中的流体密度，本文称之为密度无关型阻尼源项，该系数数值上等于液相流体密度。相应地将式(6)所示的阻尼源项称作密度依赖型阻尼源项。

2 算例设置

计算域为长400 m、高35 m的矩形区域，如图2所示，其中静水深25 m。左侧边界设置为速度入口，右侧与顶部边界设置为压力出口，底部边界设置为无滑移壁面。时间步长取0.005 s。

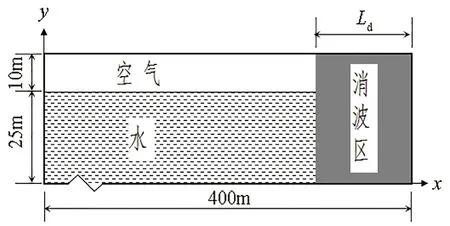
图2 计算域示意图

分别在大、小波陡条件下采用各种形式的阻尼源项开展波浪数值模拟。小波陡条件下，波高H=1 m，波长L=50 m，消波区长度Ld=50 m；大波陡条件下，波高H=2 m，波长L=40 m，消波区长度Ld=80 m。计算条件如表1所示。

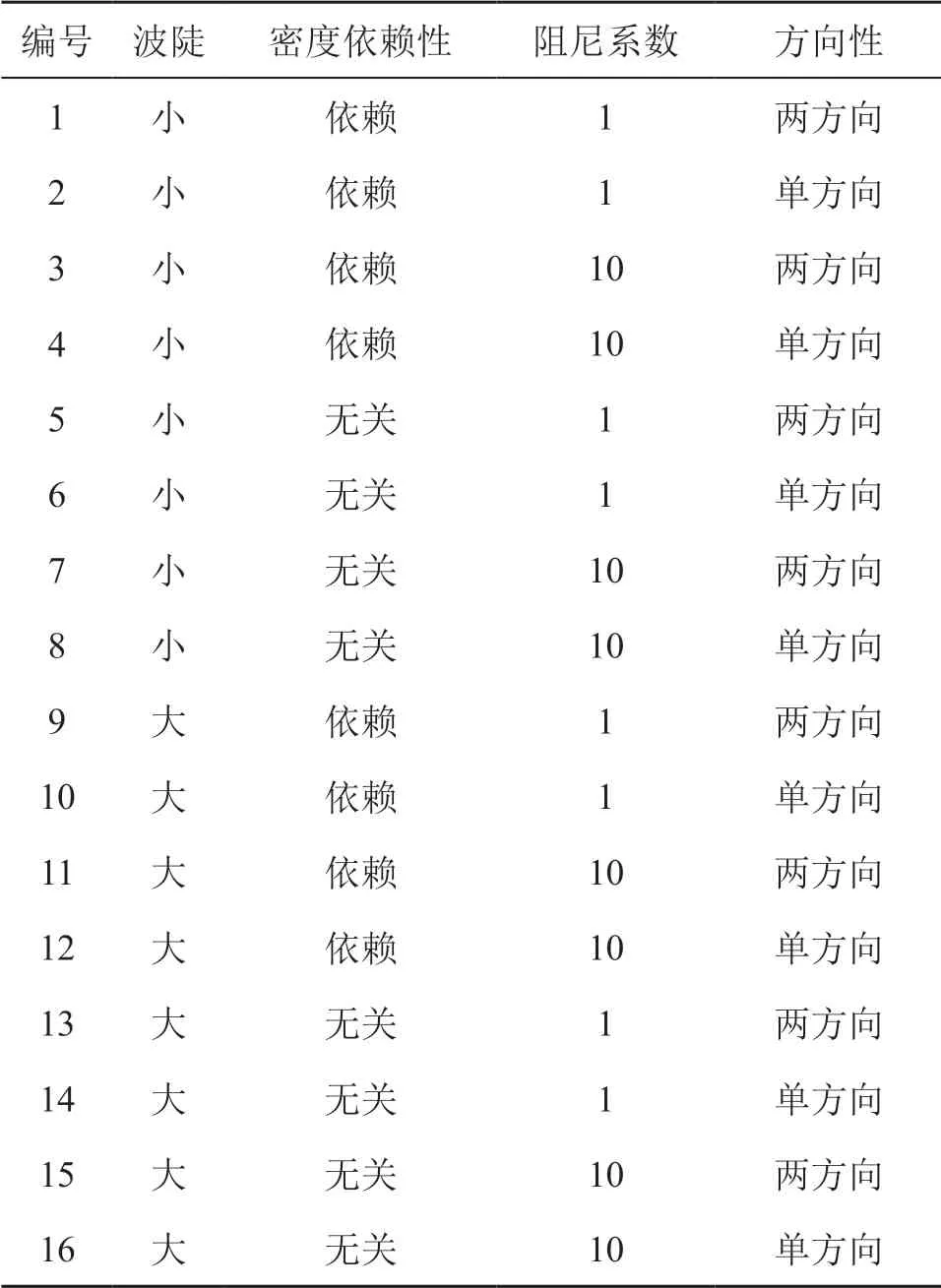
表1 计算条件

3 结果与分析

3.1 单方向阻尼源项改进效果

3.1.1 平均自由面抬升 比较采用不同方向性阻尼源项获得的数值波面，如图3所示，黑色虚线对应两方向阻尼源项，红色实线对应单方向阻尼源项。与两方向阻尼源项相比，采用单方向阻尼源项获得的数值波面在小波陡条件下略有降低，在大波陡条件下降低明显。

图3 不同方向性算例的数值波面对比

为定量分析，取观察区间内平均波峰高度与平均波谷高度的算术平均值表征平均自由面高度：

式中：m、n分别为观察区间内波峰或波谷的个数；yi,cj、yi,tj分别表示算例i中第j个波峰或波谷的高度。观察区间定义为2～5倍波长范围，即小波陡条件下取为100～250 m，大波陡条件下取为80～200 m。

比较采用不同方向性阻尼源项获得的平均自由面高度，如表2所示。相较于两方向阻尼源项，采用单方向阻尼源项可使平均自由面高度下降60%～80%，抑制平均自由面抬升效果显著。

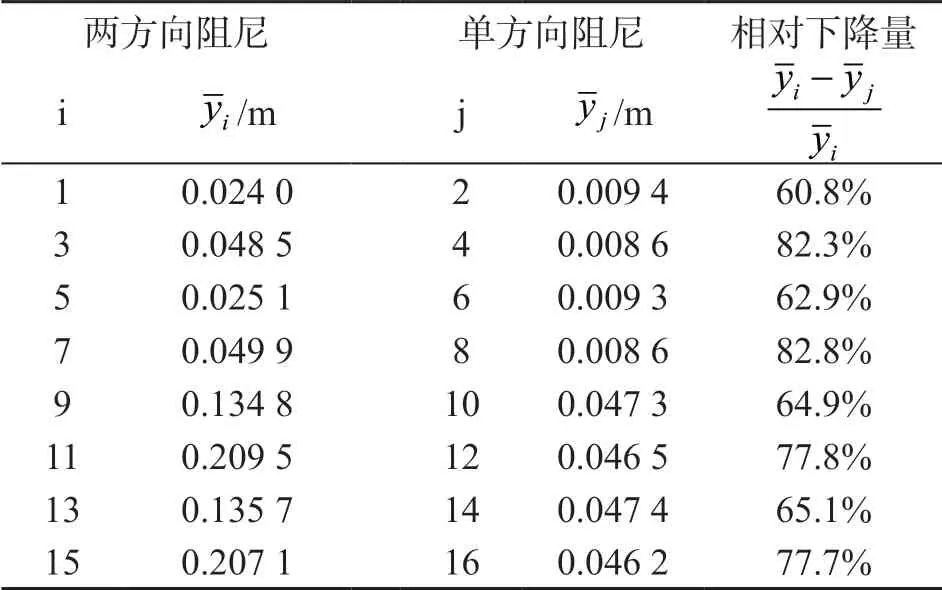
表2 不同方向性算例的平均自由面高度对比

3.1.2 波浪模拟精度 为评价波浪模拟精度，定义自由面高度数值解与解析解的偏差平方和为：

式中：η表示自由面高度；n表示数值解；a表示解析解；i=1,2…表示观察区间内沿水平方向分布的各离散点。偏差平方和越小，表示模拟精度越高。

不同方向性阻尼源项的偏差平方和对比如图4所示，黑色实心条柱对应两方向阻尼源项，红色斜纹条柱对应单方向阻尼源项。保持其他条件不变，采用单方向阻尼源项的偏差平方和普遍较小，表明采用单方向阻尼源项抑制平均自由面抬升，可提高波浪模拟精度，获得更接近波浪理论解析解的数值波面。

图4 不同方向性算例的偏差平方和对比

3.2 阻尼系数影响

比较采用不同系数阻尼源项的偏差平方和，如图5所示。图中黑色实心条柱对应μ0=1算例，红色斜纹条柱对应μ0=10算例。小波陡条件下，取μ0=1的偏差平方和较小；大波陡条件下，取μ0=10的偏差平方和较小。阻尼系数对波浪模拟精度的影响在大、小波陡条件下相反，原因在于：大波陡条件下，波浪能量较强，消波所需阻尼较大，故取μ0=10模拟精度较高；小波陡条件下相反，波浪能量较弱，取μ0=1产生的阻尼较合适，模拟精度较高。

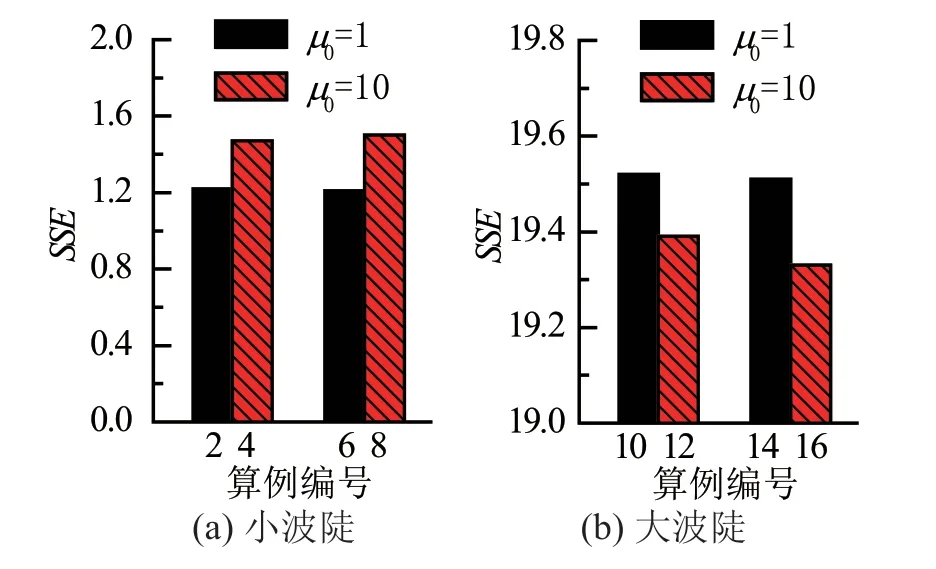
图5 不同阻尼系数算例的偏差平方和对比

3.3 密度依赖性影响

比较采用不同密度依赖性阻尼源项的偏差平方和，如图6所示。图中黑色实心条柱对应密度依赖型阻尼源项，红色斜纹条柱对应密度无关型阻尼源项。与采用不同阻尼系数相比，采用不同密度依赖性的偏差平方和相差不大，说明密度依赖性对波浪模拟精度的影响小于阻尼系数。

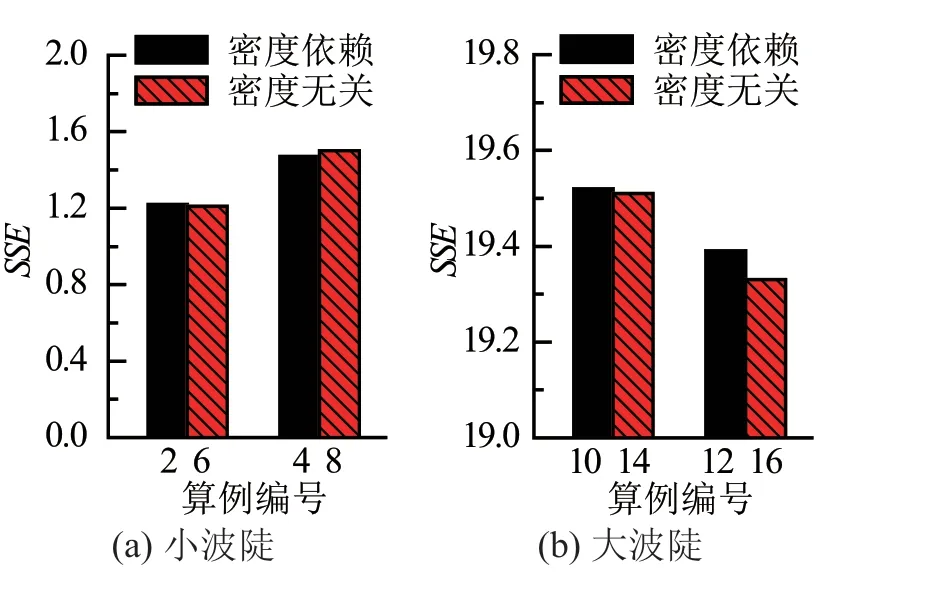
图6 不同密度依赖性算例的偏差平方和对比

尽管两者差异较小，但仍可以看出：小波陡条件下，密度依赖型阻尼源项的偏差平方和较小；大波陡条件下，密度无关型阻尼源项的偏差平方和较小。阻尼源项依赖密度与否主要影响消波区内气相阻尼大小，其中密度无关型阻尼源项产生较大的气相阻尼。如前所述，大波陡波浪能量较强，消波所需阻尼较大，故大波陡条件下密度无关型阻尼源项波浪模拟精度较高。相反，小波陡条件下波浪能量较弱，消波所需阻尼较小，密度依赖型阻尼源项模拟精度较高。

4 结 论

基于VOF模型与边界条件造波法，采用不同方向性阻尼源项在大、小波陡条件下开展了波浪数值模拟，定量比较了平均自由面抬升程度，并进一步研究了阻尼系数与密度依赖性对波浪模拟精度的影响，结果分析表明：（1）采用基于单方向阻尼源项的数值消波方法，可有效抑制平均自由面抬升，提高数值模拟精度，获得更接近理论解的数值波面；（2）阻尼系数的优取值与波陡有关，波陡较大时，消波所需阻尼较强，阻尼系数取值偏大，波浪模拟精度较高；相反，波陡较小时，阻尼系数取值也应较小；（3）密度依赖性对波浪模拟精度的影响弱于阻尼系数，小波陡条件下，密度依赖型阻尼源项模拟精度较高；大波陡条件下，密度无关型阻尼源项模拟精度较高。