点吸收式波浪能摩擦纳米发电系统输出性能的仿真研究

张 迪，林忠华,3*，杨绍辉,2,3，李 晖,2,3，蒋清山,3，肖国红,3

（1. 集美大学 机械与能源工程学院，福建 厦门 361021；2. 福建省能源清洁利用与开发重点实验室，福建 厦门 361021；3. 海洋可再生能源装备福建省高校重点实验室，福建 厦门 361021）

随着全球化石能源的日益消耗，寻求新的能源获取方式成为人们关注的焦点。传统方式获取机械能转化为电能得到了飞速发展，但是波浪能发电技术却发展缓慢[1]。波浪能开发利用方法根据收集原理可分为：点吸收式（振荡浮子式）、筏式、振荡水柱式、越浪式、摆式、点头鸭式等[2]。目前国内研制的点吸收式波浪能发电装置有：中山大学利用齿轮齿条传动研制的一种点吸收波浪能发电装置，山东大学研制的120 kW“山大一号”，中科院广州能源所研制的岸式振荡浮子发电站，中国海洋大学研制的10 kW组合型振荡浮子波浪能发电装置，浙江海洋大学研制的“海院一号”，集美大学发电研制的“集大一号”波浪能发电平台，以及在“集大一号”平台基础上改进的，利用液压系统进行能量传递的“集大二号”和新建造的半潜式“集大三号”波浪能发电平台。国外点吸收式波浪能发电装置主要有加拿大Finavera公司按照阵列布置设计并建成的42座Aqwa Buoy波浪能装置，爱尔兰研制的Wavebob装置，美国俄勒冈州立大学研制的10 kW点吸收波浪能发电装置，英国的阿基米德波浪摆（AWS）和丹麦的Wave Star阵列式波浪能发电装置等[3-5]。波浪能转换传递方式有机械齿轮式、液压式、直线电机式和磁流体式等，上述能量转换装置结构的复杂性大大限制了波浪能装置的小型化和微型化发展。2012年，王中林院士提出了一种新型发电方式——摩擦纳米发电机（TENGs），相比于传统的机械能捕获方式，摩擦纳米发电机具有结构简单、成本低、绿色无污染、输出电压高等特点。另外，摩擦纳米发电机是基于摩擦生电和静电感应相结合的原理将机械能转化为电能的新型发电方式，可有效地将波浪能转化为电能[6-7]。

本文提出了一种基于点吸收的波浪能摩擦纳米发电系统，该系统由振荡浮子、具有纳米摩擦层的连杆套筒和固定在海底的支架组成。摩擦纳米发电机采用垂直滑动模式，其两个摩擦层采用聚二甲基硅氧烷（PDMS）薄膜和铝(Al)作为接触摩擦的材料，并利用仿真模型分析了垂直滑动摩擦模式摩擦纳米发电机（TENGs）的电能输出特性，为该装置的造波水槽实验和实海况海试提供理论基础。

1 理论模型

1.1 系统的结构介绍及工作原理

本文提出的理想模型是利用波浪能进行摩擦发电。如图1 (a)所示，外部有4根脚架作为支撑固定到海底，采用垂直滑动摩擦方式进行发电，它采用套筒式连杆，上部较粗的套筒固定在上平板，下部较细的连杆连接浮子。在较细的连杆外壁先涂一层绝缘材料，然后在绝缘材料上镀一层光滑的Al电极，在较粗的连杆内侧也是先涂一层绝缘材料，再在绝缘材料上镀一层光滑的石墨电极，最后在Al电极表面黏贴一层PDMS薄膜，再用导线把两个Al电极连接到负载。在此装置中Al电极不但作为电路电极，也作为摩擦层。图1 (b)为装置的三维图。

图1 点吸收式波浪能摩擦纳米发电机

该装置通过脚架固定在海底，浮子受到波浪的作用进行上下振荡，从而带动连杆运动，浮子静止在水面时套筒内的两个摩擦层是重合的，如图2(a)所示连杆上的电极1（Al电极）会在套筒内部的介电层（PDMS薄膜）进行往复性摩擦。如图2(b)所示设极板和介电层在垂直方向长度均为l，垂直方向分离的距离为x，介电层的厚度为d。当浮子在波浪作用下向上运动时，电极1与介电层分离时，由于摩擦生电，在介电层分离区域的表面均匀分布着电荷密度为-σ的摩擦电荷，而电极1表面分布着极性相反且等量的电荷，因此在开路状态下，电极2（石墨电极）的电荷总量为0，随着浮子向上运动摩擦距离增大，电极1需要更多的正电荷来平衡接触电场，所以当用导线连接外部负载电路时，电子会由电极1流向电极2，产生电流对外做功。当浮子往上运动到最顶点时，此时两个电极的电势差最大，电极1聚集的正电荷达到最大值，浮子从位移的最顶点慢慢往下运动时，摩擦层之间的接触面积增大，电极1上聚集多余的正电荷，此时电子会从电极2流向电极1，两个摩擦层重合时，电势差为0。浮子继续向下运动，由于摩擦发电只与摩擦的距离大小有关，所以以摩擦层重合时为对称点，电极1向上运动和向下运动摩擦发电的情况是一样的。

图2 摩擦纳米发电机内部构造图

1.2 点吸收式波浪能振荡理论

假设流体为理想不可压缩的无粘性流体，当浮子振动时波浪运动无旋，如图3所示H(t)为浮子重心的位移；h0为浮子在静水平面以下的高度，浮子在波浪作用下上下振动，波浪假定为规则波，波浪的波面方程为：

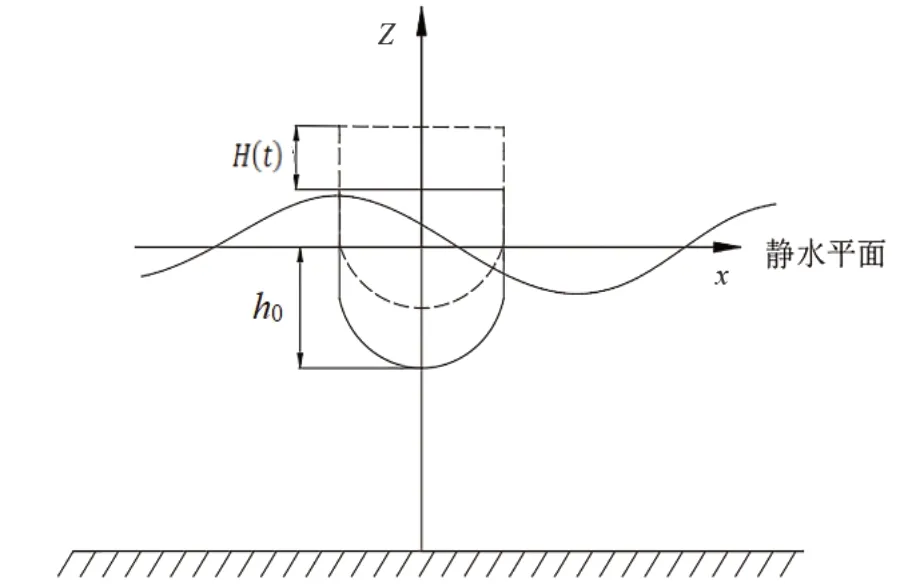
图3 浮子升降示意图

式中：A为波浪振幅；ω为波浪圆频率，当浮子的直径远小于波浪长度L时，浮子对波浪场的运动形式的影响可以忽略不计，根据线性波理论，速度势函数φ可以表示为[8]：

式中：k为波数，波传播一个波长，水质点振荡一周g为重力加速度。根据牛顿第二定律可得浮子的运动方程可以表示为[9]：

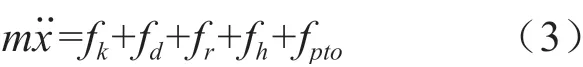
式中：m为浮子的质量；为浮子在垂直方向的运动加速度；fk为弗洛德-克雷洛夫力，即波浪入射力；fd为绕射力；其中入射力fk加绕射力fd等于波浪激励力fe；fr为辐射力；fh为静水恢复力；fpto是能量输出装置（PTO）产生作用于浮子的垂直负载。

在规则波中，波浪激励力可以表示为：

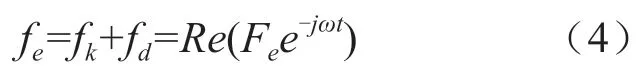
式中：Re表示取其实部，设{x,fe}=Re({X,Fe}e-jωt)，X、Fe为位移和波浪激励力的复数模，由于浮子在X轴方向的尺寸远小于入射波的宽度，根据文献[10]Fe为波浪激励力的振幅可大致表示为：

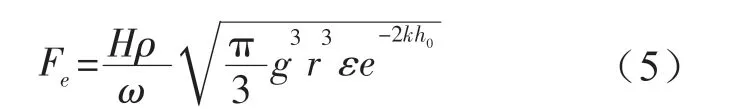
式中：H为自由波面高度；ρ为水的密度；ε为阻尼系数，r为浮子的半径。

辐射力fr与浮子的运动加速度和速度有关，因此可以表示为：

式中：B是浮子在流体中由于运动而使得周围流体一起运动产生的附加质量；C是关于波浪频率的辐射阻尼系数；，分别为浮子在垂直方向的速度和加速度。辐射阻尼系数可近似表示为[10-11]：

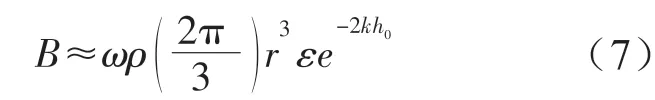
静水恢复力fh是浮子排开液体的重量与自身重量之差，可以表示为：

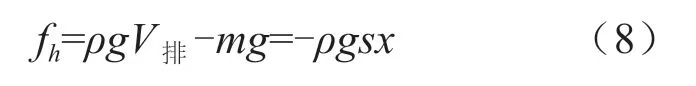
式中：V排为浮子排开液体的体积；s为浮子吃水线处的浮子截面面积。

由于本文所提出的点吸收式摩擦纳米发电机能量输出装置（PTO）没有液压油缸等结构，只有摩擦层之间的摩擦力，所以fpto=–μN，μ为PDMS摩擦层的摩擦系数；N为PDMS摩擦层与套筒内侧电极之间的正压力。所以由公式（3）得：

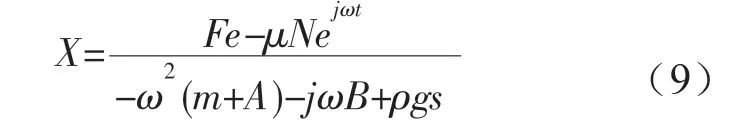
由于套筒和连杆的尺寸是固定的，连杆外侧的PDMS介电层和套筒内部的电极1之间处于刚好接触到间隙配合之间，它们之间的正压力N接近于0，所以PDMS介电层与电极1之间的摩擦力可以忽略不计。运动时电极之间产生电场，PDMS介电层随着电极2一起运动，在电场作用下它靠近电极两侧会分布等量的异性电荷，其整体处于静电屏蔽状态，且不切割磁感线，即不会产生电磁阻尼力，所以浮子在垂直方向运动近似看作自由振荡。所以公式（9）可以写成：

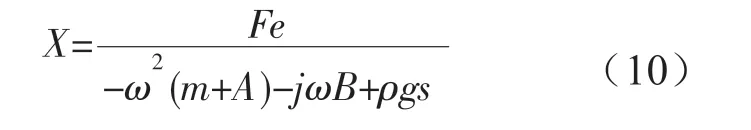
从式（10）可以看出浮子在垂直方向的自由振荡与波浪激励力、波浪频率、浮子质量、附加质量、辐射阻尼系数、浮子吃水线处截面面积等有关。Jeffery基于傅里叶变换对波浪能发电装置的浮子振荡情况进行了时域分析，其运动方程为：

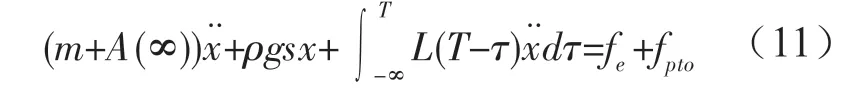
1.3 滑动式摩擦纳米发电机理论

在推导垂直滑动模式TENGs的理论表达式时，考虑到实际情况l（极板和介电层长度）总是比d（介电层厚度）的数量级大得多，况且当两个摩擦层完全分离后很难回到原来的状态而不损坏介电层，所以在实际应用中垂直分离的距离x要小于等于0.9l，使得两个介电层有个重叠区域，便于下次的往返运动；介电层的厚度与其长度相比小得多，只要两个摩擦层没有完全分离，总电容就由重叠部分区域的电容决定，设定d0为有效厚度常数，为相对介电常数，电容C的表达式为：

这里的ε0为空气介电常数；w为PDMS介电层的宽度；x为电极1的位移也就是浮子的位移，取向上运动为正，向下为负，系统的摩擦发电只与电极1位移的大小|x|有关，与位移的方向无关。

如图2(b)所示，对于电极2未重叠区域电荷密度为：

式中：σ代指电荷密度的数值。

对于电极2重叠区域电荷密度为：

对于电极1未重叠区域电荷密度为：

对于电极1重叠区域电荷密度为：

根据上面的式子可以推导出开路电压Voc的表达式为：

短路时转移电荷量为：

短路电流为：

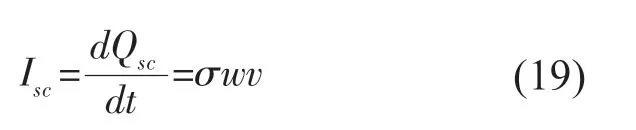
式中：v是|x|对时间t的导数。

连杆套筒之间的滑动摩擦是利用波浪的上下振动，设定波浪频率为0.2 Hz，波浪高度分别为0.3 m、0.35 m、0.4 m、0.45 m、0.5 m，利用水动力软件AQWA对浮子的上下振动位移进行仿真，为了确保仿真的可靠性，垂直分离的距离x的绝对值要小于等于0.9l。

2 仿真分析

2.1 点吸收波浪能装置的振荡仿真分析

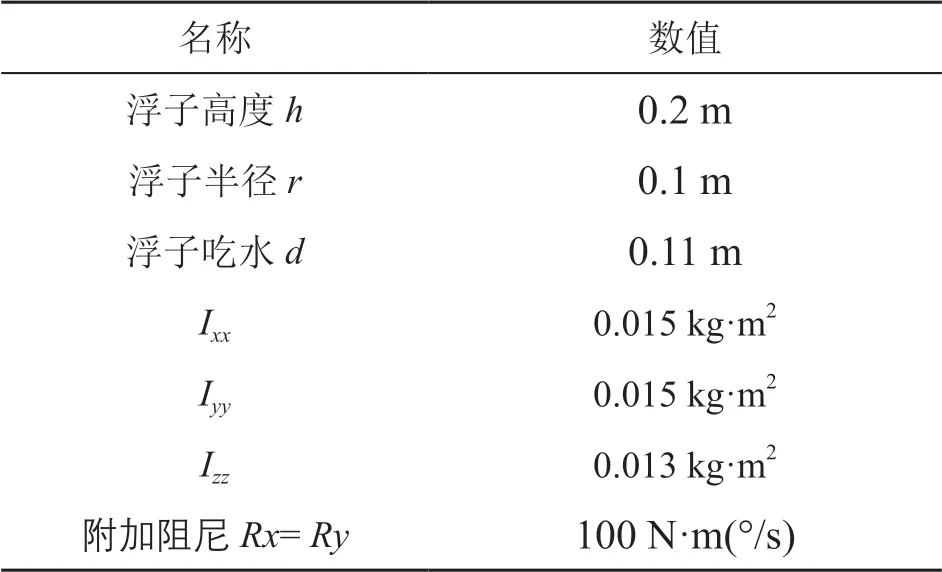
表1 用于浮子位移仿真的主要参数

对点吸收装置进行简化建模，只保留了浮子部分，浮子在z轴方向上下振动，浮子本身的质量为2.85 kg，浮子表面会受到入射波的影响，在浮子表面的压强分布不一样，如果没有约束的话，浮子会产生翻滚现象，本文仿真只要求在垂直方向运动，所以在X轴设置旋转的附加阻尼Rx=100 N·m(°/s)，在Y轴方向同样设置旋转阻尼Ry=100 N·m(°/s)，来防止浮子发生翻滚；由于能量输出装置（PTO）的摩擦阻力非常小，所以在垂直方向的PTO阻尼设置为0。具体建模过程如下。

（1）利用SolidWorks进行浮子的三维建模，并把模型转化成XT格式；然后打开ANSYS中的workbench界面；（2）把建好的模型导入Design Modeler，按照吃水线把模型分割成两部分，再进行抽壳，厚度设为0；（3）设置海域面积为S=100 m×100 m，水深15 m，重力加速度9.8 m/s2，浮子吃水深度0.11 m，计算浮子中心，设置中心位置；（4）设置附加阻尼Ry=Rx=100 Nm(/s)；（5）对浮子进行网格划分，设置最大网格尺寸为0.01 m，最小绕射单元网格尺寸为0.004 m；（6）将AQWA频域计算部分的波浪频率设为100份，时域计算部分的规则波波高0.5 m，波浪周期5 s，计算时长为60 s，步长为0.05，波浪入射方向与x轴呈180°。

图4所示为波浪频率0.2 Hz时，不同波浪高度下的浮子位移，是以浮子重心为位移0点，向上位移为正，向下位移为负，由于是浮子的上下振动使得套筒内的摩擦层进行上下往复摩擦，所以下文中的摩擦位移与浮子位移是一致的。

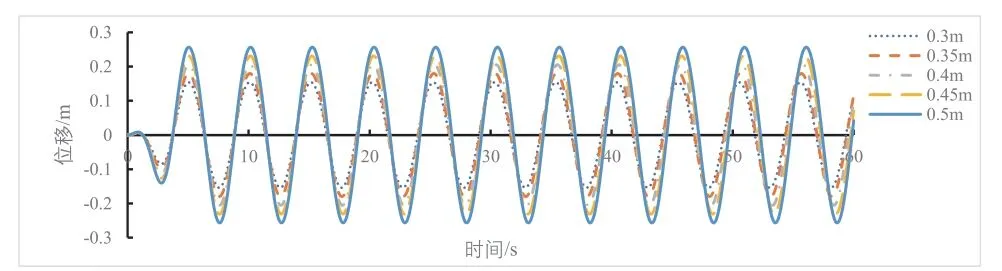
图4 波浪频率0.2 Hz，不同波浪高度下浮子的位移

2.2 不同波浪高度下TENGs输出特性的仿真分析

将AQWA仿真得到的浮子位移数据导入数学仿真模型中，然后对摩擦纳米发电机TENGs的输出性能进行仿真分析，表2为摩擦纳米发电机仿真时的具体参数。

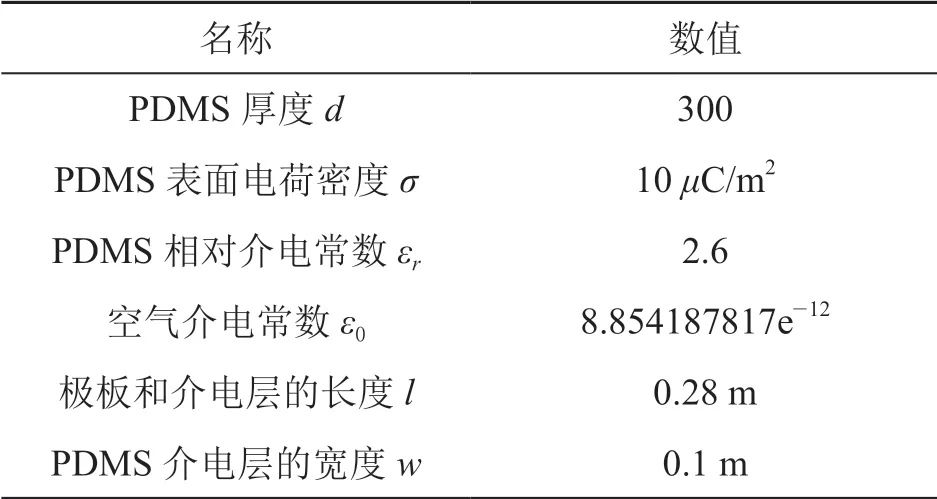
表2 摩擦纳米发电机用于仿真时的各项参数[12]

浮子的上下振荡情况就是摩擦纳米发电机PDMS介电层和Al电极的相对运动情况，仿真分析结果显示，不同波浪高度下的开路电压、转移电荷量、电容和短路电流的变化与绝对摩擦位移|x|的大小有对应，波浪高度影响到绝对摩擦位移|x|的最大值，当不同波浪高度下的绝对摩擦位移|x|相等时，开路电压、转移电荷量、电容和短路电流是一样的，在图5至图7中，波浪高度0.3 m的数据会依次被波浪高度0.35 m、0.4 m、0.45 m、0.5 m的数据所覆盖。根据开路电压公式求得开路电压与位移的关系，摩擦位移x有正有负，但是摩擦层只要有相对位移就能产生电压，摩擦位移x向上为正，向下为负，当摩擦位移x值为正时，摩擦位移x从0到最大值（最高点）时，电极1需要更多的正电荷来平衡接触电场，电流从电极2流向电极1。摩擦位移x从最大值（最高点）返回到0时，电极2的电势高于电极1的电势，电流从电极1流向电极2，当摩擦位移x为负时，发电情况和摩擦位移x为正时一样，只与绝对摩擦位移|x|有关，从图5可以看出绝对摩擦位移|x|值越大，相应的开路电压越大。不同波浪高度下，只要绝对摩擦位移|x|相同，产生的开路电压就相同，从图2上解释为电极1和PDMS介电层重叠的部分越小对应的开路电压越大，且波浪高度越大，最大开路电压也越大。从图6可以看出波浪高度0.5 m时短路时转移电荷量与位移呈正比关系，只要绝对摩擦位移|x|相同，转移电荷量就相同，绝对摩擦位移|x|值越大，转移的电荷量也就越大，且波浪高度越大，最大转移电荷量也越大。图7显示电容随绝对摩擦位移|x|变大而减小，位移为0时，也就是电极1与PDMS介电层完全重合时电容最大，最大为2.09 nF。从图8可以看出浮子运动规律后，短路电流随位移x的变化呈封闭曲线，在封闭曲线的内部是浮子从刚开始运动到还未达到稳定的周期性运动期间短路电流的变化，图8的曲线对应的振荡摩擦发电的顺序是从坐标轴原点开始向外做顺时针旋转，波浪高度越大，浮子振荡稳定后封闭曲线所包围的面积越大，同样在浮子振荡稳定后，摩擦位移为0时，短路电流最大，摩擦位移达到波浪最大振幅时，短路电流为0。图9(a)为浮子在振荡稳定前的短路电流随摩擦位移的变化情况，图9(b)为浮子振荡稳定后短路电流随摩擦位移的变化情况。

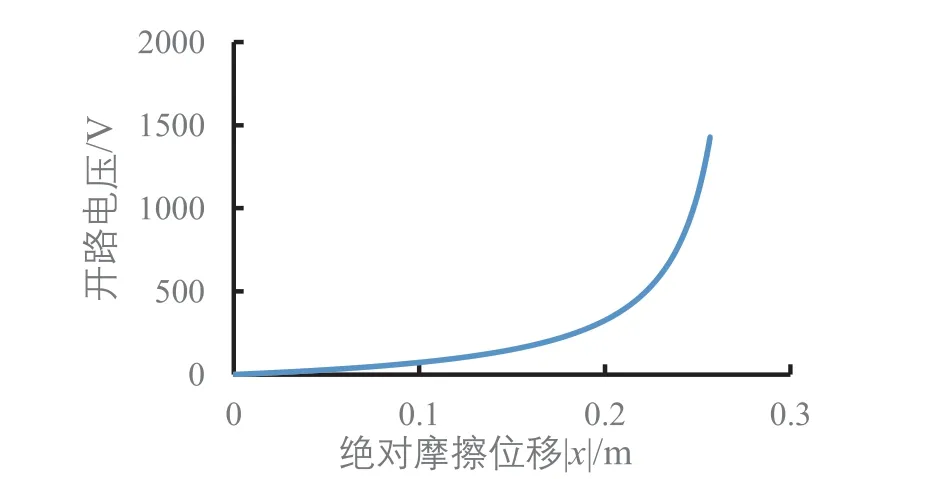
图5 波浪高度0.5 m下开路电压随摩擦位移的变化

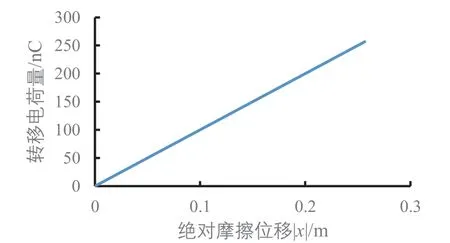
图6 波浪高度0.5 m下短路时转移电荷随摩擦位移的变化

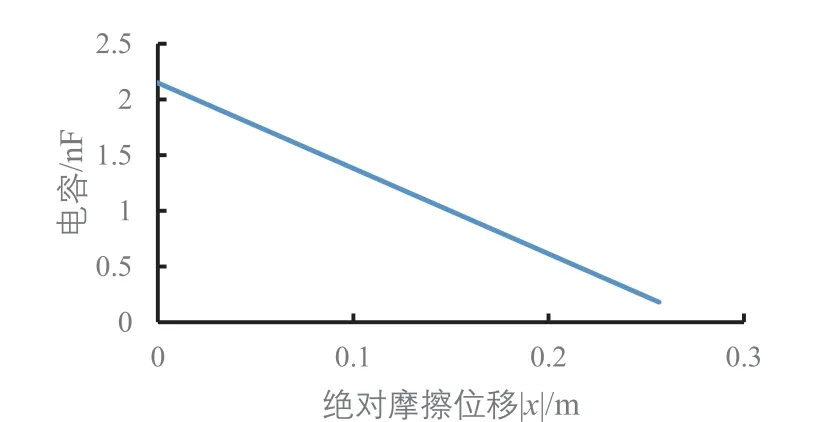
图7 波浪高度0.5m下TENGs的电容随摩擦位移的变化

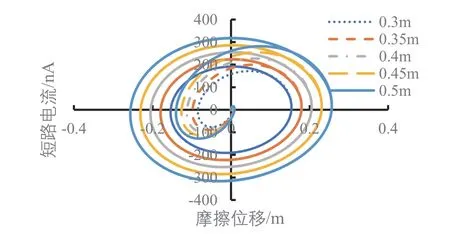
图8 不同波浪高度下短路电流随摩擦位移的变化

图9 不同波浪高度下浮子振荡的短路电流随摩擦位移的变化情况

本文研究在波浪频率为0.2 Hz、不同波浪高度下TENGs的输出特性的随时间的变化规律，从图10可以看出，随着波浪高度的增加，开路电压也随之增大，并且当浮子运动规律后，电压输出也呈现规律变化，并且频率变为0.4 Hz，周期为2.5 s，是波浪周期的一半，原因是电极1与PDMS介电层重叠部分是l-|x|。图10可以看出在波浪高度为0.3 m的基础上每增加0.05 m，电压输出稳定后最大开路电压增加量也会随着波浪高度的增加而增加。图11曲线对时间的导数就是图12，转移电荷量和短路电流都随着波浪高度的增加而增加，它们的周期也和开路电压一样为2.5 s。图13为不同波浪高度下电容随时间的变化情况，可以看出在0～3 s内电容值曲线与后面的曲线不同，是因为浮子受自身惯性影响，还未达到规律的运动，浮子达到规律的运动后电容曲线也呈规律的周期变化。最大电容值不随波浪高度的变化而变化，最大电容为电极1与PDMS介电层完全重合时，最大为2.09 nF，最小电容随着波浪高度的增加而减小，是因为波浪高度增加电极1与PDMS介电层最大重叠距离l－|x|减小，所以最小电容减小。

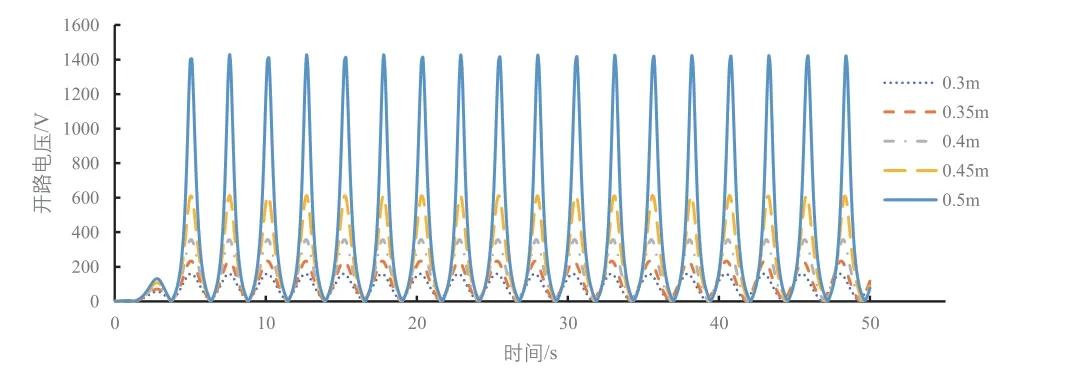
图10 不同波浪高度下的开路电压

图11 不同波浪高度下的转移电荷量

图12 不同波浪高度下的短路电流

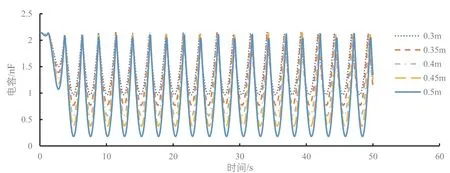
图13 不同波浪高度下的电容

图14至图17是对图10至图13的图形特征做了进一步分析。图14显示波浪高度增加时最大开路电压呈抛物线趋势增大。图15和图16规律一样，最大转移电荷量和最大短路电流随波浪高度的增加基本呈线性增加。图17直观地显示了最小电容随波浪高度的增加呈线性减小。

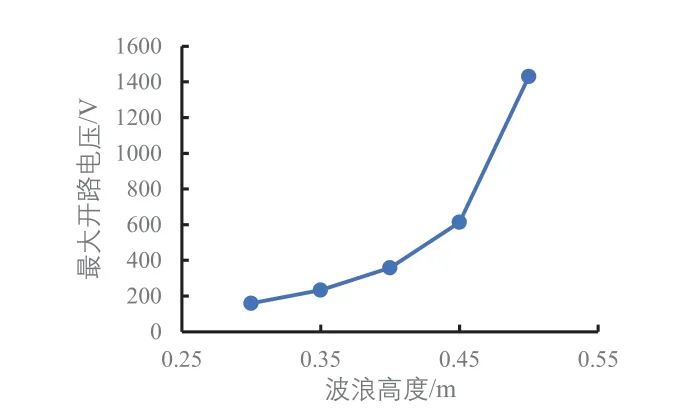
图14 不同波浪高度下的最大开路电压

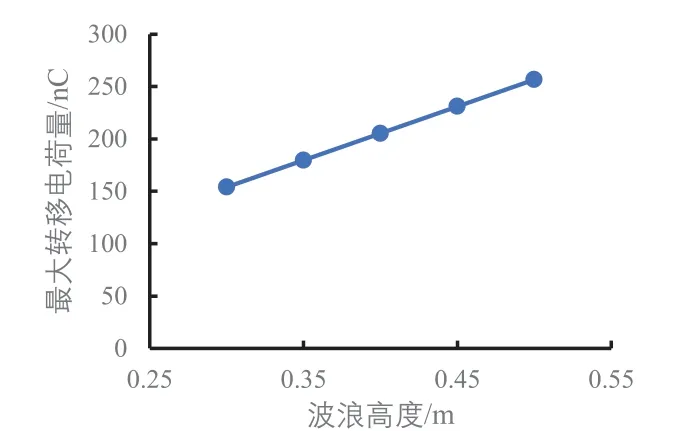
图15 不同波浪高度下的最大转移电荷量

图16 不同波浪高度下的最大短路电流

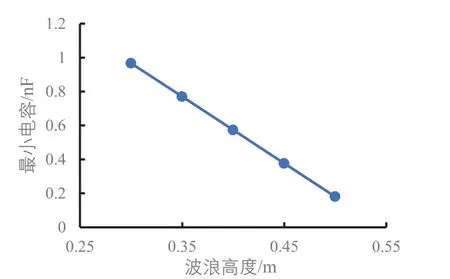
图17 不同波浪高度下的最小电容

图18为不同波浪高度下摩擦纳米发电机在不同外接负载下峰值电压和在峰值电压下对应的功率与电流，从图可以看出功率会随着负载电阻的变化而变化，在109Ω附近会出现最大功率，并且功率曲线会随着波浪高度的增加而变大。负载两端会产生随时间变化的电压，最大电压即峰值电压会随着负载的变大而逐渐变大，并且波浪高度的增加也会引起峰值电压的变大。电流在数值上等于功率与峰值电压的比值，电流整体是随着负载阻值的增加呈下降趋势，并且波浪高度对负载电流的影响不大。

图18 不同波浪高度下电能输出特性随负载阻值的变化

3 结 论

本文提出了一种点吸收式波浪能摩擦纳米发电装置，该装置利用波浪驱动浮子进行上下振荡，从而带动连杆套筒内的纳米摩擦发电机进行摩擦发电，通过对点吸收式摩擦纳米发电机进行仿真分析，改变波浪高度和外接负载的阻值研究其电能输出特性，研究结果表明。

（1）电能输出稳定后，电容随着绝对摩擦位移|x|的增加呈线性减小，转移电荷量随着绝对摩擦位移|x|的增加呈线性增加，而开路电压随绝对摩擦位移|x|的增加呈现抛物线似的增加。

（2）在波浪高度增加时，电能输出稳定后开路电压、短路电流和转移电荷量也会相应增加，最大开路电压增加量也会呈抛物线趋势增加，最大转移电荷量和最大短路电流随波浪高度的增加基本呈线性增加。

（3）在波浪高度增加时，电能输出稳定后电容的最大值不会随波浪高度的变化而变化，最小电容随着波浪高度的增加而呈线性减小。

（4）电能输出稳定后，开路电压、短路电流、转移电荷量和电容的曲线周期变为波浪周期的1/2。

（5）负载两端的功率和电压会随着波浪高度的增加而增加，并且负载两端的峰值电压随阻值的增加而变大，功率会随阻值的增加出现一个峰值，其最佳匹配电阻在109Ω左右，此时摩擦纳米发电机的发电性能最佳，对应波浪高度为0.5 m时最大发电功率为173.6μW。

本文对点吸收式波浪能摩擦纳米发电装置进行了理论仿真研究，为下一步实验提供了理论支持。摩擦纳米发电机的材料属性和装置的防水性能是制约装置发电因素，将是未来研究的方向之一。