基于一维气体单流体模型的天然气-凝析液管道流体流动预测

张璐瑶 路宏 陈宏举， 周良胜 李鹏程 王玮 宫敬

1中国石油大学（北京）城市油气输配技术北京市重点实验室·油气管道输送安全国家工程实验室

2中海石油（中国）有限公司北京研究中心

随着油气勘探开发从陆地走向深海、沙漠等地处偏远及环境复杂的地区，恶劣的生产环境促使油气混输技术应用更加广泛。稳定并准确地获取油气管道相关运行参数（压力、流速、温度等），对油气集输管道的设计及安全运行管理具有重要意义。

国内外学者对气液两相流进行了大量的研究[1-8]，但是气液两相流的数值模拟仍不成熟。对于存在相变的天然气-凝析液管道，因其涉及相间质量传递、动量和能量传递，通常采用均相流模型[9]、漂移流模型[10]和双流体模型[11]进行描述和流动预测。均相流的简化过于理想，计算结果与实际相差较大。漂移流模型中含有相关式，导致适用范围较窄。双流体模型是在充分考虑两相流各相流动主要特征的基础上建立的，相对更加稳健且使用广泛，但学者指出采用双流体模型时模型的双曲性[12]非常重要，模型不适定将产生不符合流动规律的预测结果。然而，双流体模型并不是无条件双曲的，为保证方程的双曲性，一些学者在控制方程中增加压力松弛输运方程[13]、虚拟质量力[14]、界面压差[15]等，但因没有明确的物理意义而存在争议。

考虑到上述情况，针对低持液率天然气-凝析液管道内液体和气体的自身流动特点，在一维瞬态双流体模型基础上，建立了一维瞬态气体单流体简化模型。该模型可以避免计算过程中由于相的出现与消失而带来的计算不稳定问题，并进一步补充封闭关系以及热力计算，讨论了一维瞬态非等温可压缩气体单流体模型用于低持液率天然气-凝析液管道内流体流动预测的适用性。

1 模型理论

1.1 控制方程

流体流动时假设忽略各参数在截面分布的不均匀性[16]。基于质量守恒定律、动量守恒以及能量守恒定律，对截面上的流动参数进行积分，得到一维瞬态非等温可压缩气体单流体模型[17]。

连续性方程：

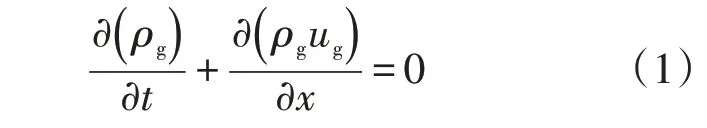
动量方程：

温度方程[6]：

定压比热和JT系数分别定义为[6]：

式中：ρg为气相的密度，kg/m3；ug为气相的速度，m/s；p为压力，Pa；g为重力加速度，m/s2；θ为管道倾角；τg为剪切应力，N/m2；Sg为天然气润湿周长（即为管道截面周长），m；A为横截面积，m2；cpg为定压比热容，J/(kg·K)；αhg为JT效应系数；U为流体与外界总换热系数，W/(m2·K)；D为管径，m；Te为环境温度，K。

1.2 封闭关系

剪切应力由摩阻系数与动能的乘积表示。

气体与管壁的摩阻系数根据ISSA[1]推荐，层流时采用Hagen-Poiseulle关系式，湍流时采用Taitel-Dukler[18]关系式。

2 数值求解

2.1 数值离散

在节点设置上采用内节点法，采用交错网格（图1），实线表示主网格，虚线表示交错网格。在交错网格中，标量设置在主网格上，如压力、密度、温度；矢量设置在交错网格上，如速度[19]。对流项的离散采用一阶迎风格式，时间项的离散采用一阶隐式格式。

图1 交错网格示意图Fig.1 Schematic diagram of staggered grid

将动量方程在速度控制容积上积分得到

将温度方程在主控制容积上积分得到

公式中上标n和n+1 分别表示当前时层和下一时层。采用SIMPLE 压力修正算法[20]，基本过程为：假设初始压力为p，由动量方程可求得相应的速度u。这时的速度并不能满足连续性方程，因此需要修正，设修正量为u′。由动量方程可知，若速度变化，压力也会随之改变，因此设对应于速度修正量u′的压力修正量为p′，则新的速度与压力为

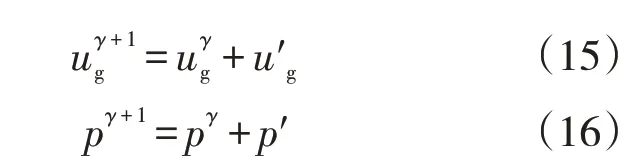
将修正前后的速度与压力代入动量方程中相减，可推导出速度修正量与压力修正量之间的关系。

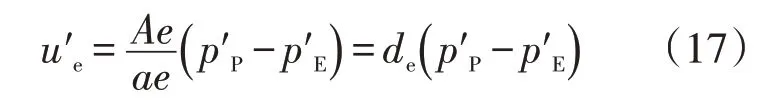
考虑气体压缩性，根据状态方程推导出密度和压力的关系式。

对于压力方程的构造，将式（15）、（16）和（17）代入式（1）连续性方程中整理后可得如下形式

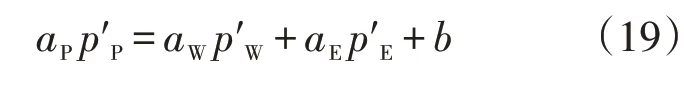
2.2 CFL 条件

为了保证数值计算的稳定性，在确定网格步长后，通常采用CFL条件来确定时间步长[21]，其描述了流体流动的距离在一个时步内不得超过一个网格的长度。设流体流速为u，网格步长为Δx，则时间步长Δt可表示为

其中CFL≤1。随着网格的细化，时间步长会相应减小，故在模拟中，需检查所有网格的CFL条件，选取最小的时间步长，作为当前的时间步长。

2.3 收敛判据

压力修正算法的基本思想是速度与压力相互修正，最终达到同时满足动量方程和质量守恒方程的目的。而压力修正方程中的源项b刚好是质量守恒方程的离散形式。如果上一迭代层次的流场满足质量守恒，则b=0。因此b反映了每一个控制容积是否满足质量守恒，可以作为一个层次迭代是否收敛的一个指标[19]，即

允许误差数值ε通常取10-3～10-6，本文取ε为10-5。

2.4 算法步骤

假定管道内流体组分是恒定的，但流体特性（如黏度、密度、气液相体积分数等）会随温度和压力变化。在此假设下，首先计算出一定压力和温度范围下流体特性参数表，计算过程中每一时步下参数根据这个表插值更新。当管道内存在液相时，则利用气液相混合物性参数（密度、黏度等）来代替气体单流体的物性参数，并将气液混合物质量流量等效为气相单流体质量流量。

算法步骤如下：

（1）由初始或上一步的压力pγ、温度Tγ更新流体参数，计算动量方程的系数与源项。

（3）求解压力修正方程（19）得到压力修正量p′，并根据式（17）得到速度修正量。

（4）根据式（15）、（16）得到修正后的压力pγ+1和速度。

（6）判断是否收敛，如果不收敛，将当前变量值作为下一层次迭代的初始值返回第一步；如果收敛，利用修正后的压力、速度和密度求解温度方程（3），得到Tγ+1，然后进入下一时步计算。

3 算例分析

3.1 基础数据

某模拟海底管道总长77.5 km，规格Φ558.8 mm×23.8 mm，其地形数据及管道周围环境温度见表1，天然气组分见表2。该算例边界条件：入口定质量流量为119.98 kg/s，入口温度为34 ℃，管壁绝对粗糙度为0.02 mm，管道总换热系数为45 W/(m2·K)，出口定压为10 MPa。

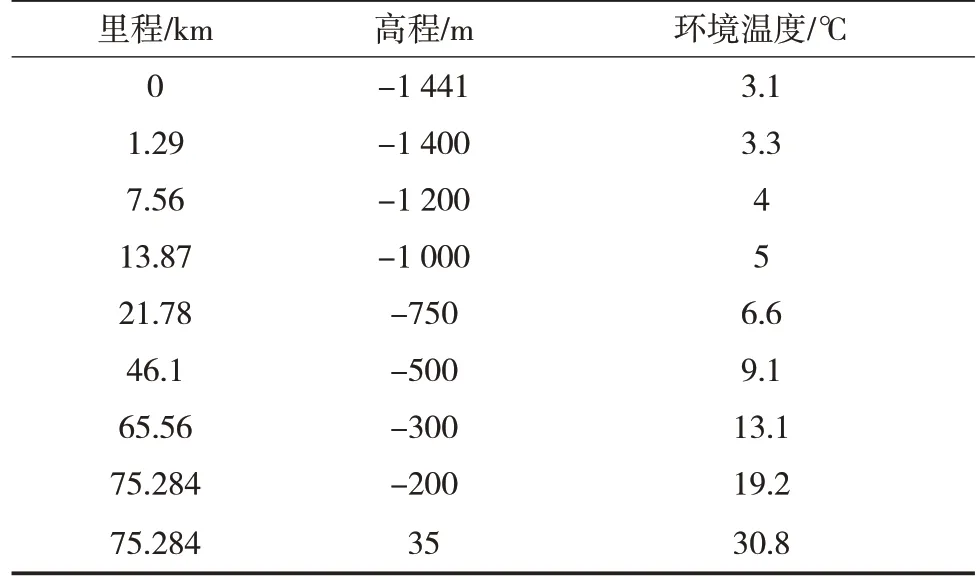
表1 模拟海底管道高程及环境温度Tab.1 Elevation and ambient temperature of simulated submarine pipeline

表2 模拟海底管道天然气组分Tab.2 Natural gas composition of simulated submarine pipeline 摩尔分数/%

3.2 计算结果

利用一维瞬态非等温可压缩气体单流体模型以时间推进的方式模拟稳定流动，此过程中每一时间步下的模拟均收敛。对于最终稳定的流场，对比了本研究与OLGA[22]对模拟管道相同运行工况下五个组分（五个组分计算得到管道中最大持液率分别为0，1%，5%，10%，20%）的流动参数计算结果（表3）。计算所得气体流速、压力、温度沿线分布对比见图2～图6。

图2 本研究与OLGA软件计算0持液率组分沿线气速、压力、温度变化Fig.2 Gas velocity，pressure，and temperature changes along the line calculated by this research and the OLGA software at 0 liquid holdup

图3 本研究与OLGA软件计算1%持液率组分沿线气速、压力、温度变化Fig.3 Gas velocity，pressure，and temperature changes along the line calculated by this research and the OLGA software at 1%liquid holdup

图4 本研究与OLGA软件计算5%持液率组分沿线气速、压力、温度变化Fig.4 Gas velocity，pressure，and temperature changes along the line calculated by this research and the OLGA software at 5%liquid holdup

图5 本研究与OLGA软件计算10%持液率组分沿线气速、压力、温度变化Fig.5 Gas velocity，pressure，and temperature changes along the line calculated by this research and the OLGA software at 10%liquid holdup

图6 本研究与OLGA软件计算20%持液率组分沿线气速、压力、温度变化Fig.6 Gas velocity，pressure，and temperature changes along the line calculated by this research and the OLGA software at 20%liquid holdup

表3 五种持液率组分在不同计算方法下的水力热力参数计算结果Tab.3 Results of hydraulic and thermal parameters of five liquid holdup components under different calculation methods

由对比结果可知：在五个算例中，本研究计算的气速、温度与OLGA结果均吻合较好。随着持液率增加，气速逐渐降低。因管道总换热系数较大，入口环境温度较低，管内流体温降主要出现在入口0～15 km位置，随后伴随周围环境温度的升高，管内流体温度逐渐回升；在立管段由于压力降低带来的节流效应将导致流体温度有明显下降。由图7可以看出，在不考虑JT 效应时，立管段的流体温度没有下降，与实际不符，而考虑JT 效应时立管段的流体温度出现明显下降，随着持液率的增加，本文计算出的终点温度逐渐下降。由于液相密度明显大于气相，故管道的入口压力随持液率的增加而增大。本研究计算的压力结果与OLGA结果趋势保持一致，但数值上略有差异。当持液率达到10%时，本研究压力计算结果与OLGA 的相对误差为4.65%，验证了采用一维瞬态可压缩气体单流体模型预测低持液率天然气-凝析液管道内流体的流动特性是可行的。本研究算例中，当持液率达到20%时，管道入口压力预测的相对偏差进一步增大。

图7 0持液率下不考虑JT效应与考虑JT效应的温度结果对比Fig.7 Comparison of temperature results without and with considering the JT effect at 0 liquid holdup

4 结论

本文采用SIMPLE 压力修正算法，开展了一维瞬态非等温可压缩气体单流体模型对低持液率天然气-凝析液管道入口压力、流速及温度的预测分析。通过某模拟海管五个不同持液率（0，1%，5%，10%，20%）算例的对比分析，验证了一维瞬态非等温可压缩气体单流体模型对低持液率天然气-凝析液管道内流体的流动预测具有适用性，可指导低持液率天然气-凝析液管道的工程计算。