腐蚀缺陷参数对管道剩余强度的影响分析

欧阳海涛，陆潇，刘宁宇，李旭海，蒋玉卓，梁昌晶

1.中海油石化工程有限公司（山东 青岛 266101）

2.中国石油长庆油田分公司 第十一采油厂（陕西 西安 710016）

3.国家石油天然气管网集团有限公司 建设项目管理分公司（河北 廊坊 065000）

4.国家管网集团西南管道有限责任公司 南宁输油气分公司（广西 南宁 541300）

5.中国石油青海油田分公司 管道处（青海 格尔木 816000）

6.中国石油华北油田分公司 第一采油厂 (河北 任丘 062552)

随着我国国民经济的快速发展，逐步形成了“西气东输”“川气东送”等一系列大型油气管道工程，管道运输成为我国主要的能源运输方式。我国的油气输送管道主要以埋地钢管为主，经过长时间的使用，受到土壤、输送介质、杂散电流等因素的影响会产生一定的腐蚀缺陷[1-2]，腐蚀缺陷不仅对管材的力学性能产生影响，同时对应力的分布也有一定作用。为了保障油气管道的正常运行，有必要对腐蚀管道的剩余强度进行评价，以期为管道完整性提供理论依据[3]。

目前，对于单一腐蚀管道剩余强度的计算和评价，主要有美国的ASME B31G 系列标准、挪威船级社的DNV-RP-F101、SY/T 6477—2000等标准，这些评价方法具有一定的实用性，但评价结果过于保守，容易造成不必要的材料更换和维修，增加维修费用。王阿敏[4]、高建华[5]、HOANG Van 等[6]均利用有限元方法对腐蚀管道的剩余强度进行了模拟计算，通过与实验结果进行验证，表明有限元能够分析管道内部的应力变化，绝对误差较小，可以适应实际工况条件下的剩余强度计算。但以上研究多集中在单一腐蚀缺陷参数对剩余强度的影响分析，没有对相关参数之间的拮抗和协同作用进行分析，对多因素之间的交互影响涉及较少。在此引入响应曲面的数学统计方法，利用响应曲面对影响因素进行实验设计，通过对模型进行方差分析，讨论各因素之间的相互作用。

1 实验方法

1.1 响应曲面法

响应曲面法的主要目的是优化响应或研究各因素与响应之间的潜在规律，是一种序贯类实验方法[7]。设响应y与各因素x1，x2，… ，xs之间存在如下关系：

式中：f为未知函数；ε 为均值为0、方差为σ2的随机误差。由于响应y和各因素之间的关系可以用s维的曲面来表示，因此称该函数为响应曲面。当实验的参数范围不大时，可以用低阶多项式函数来拟合f，通过最小平方法将其回归为一阶模型：

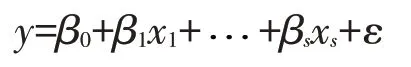
当一阶模型不合适时，必须选用二阶模型：

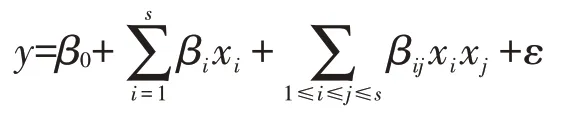
式中：β0、β1、βs、βi、βij分别为多项式的系数。

油气管道的局部腐蚀缺陷均为不规则体积型缺陷，形貌高低起伏呈丘陵状分布。在此选择最为常见的类长方体腐蚀形貌，定义缺陷长度A（轴向长度）、缺陷宽度B（周向长度）、缺陷深度C（径向长度）3个参数为自变量，管道剩余强度Y为因变量，利用Design-expert 软件进行响应曲面设计，其中实验因素和水平取值见表1。

表1 实验因素和水平取值 mm

1.2 有限元分析

以某油田实际生产数据为例，选用的直管段管材为X65管线钢，长度3 000 mm，外径529 mm，壁厚9.5 mm，抗拉强度550 MPa，屈服强度480 MPa，泊松比0.3，焊接系数取1.0。埋地管道主要受内压和轴向附加载荷的影响，其余载荷对管道剩余强度的影响不大，因此设置内压载荷6 MPa，轴向附加载荷0.5 MPa。

通过Ansys workbench 对模型进行处理，根据模型自动选择优化的网格划分方式，自行设置网格单元数量和大小，划分后的管道网格模型如图1所示。

图1 划分网格后的模型

对体积型缺陷进行分析时，需要建立一定的屈服边界条件，可以采用材料力学第四屈服强度Von Mises准则来判断管道是否失效，当缺陷区域的等效应力超过屈服强度时，认为管道失效，此时管道所能承受的内压即为管道剩余强度。Von Mises 等效应力计算公式如下：

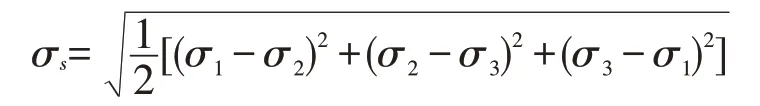
式中：σs为等效应力，MPa；σ1、σ2、σ3为单元体从大到小的3个主应力，MPa。

2 结果及讨论

2.1 模型优选及方差分析

Design-expert 软件可提供多种实验设计方法，在此采用Box-Behnken Design（BBD）的方法进行试验[8-9]。根据实验条件，通过Anysys workbench 得到15组响应结果，见表2。

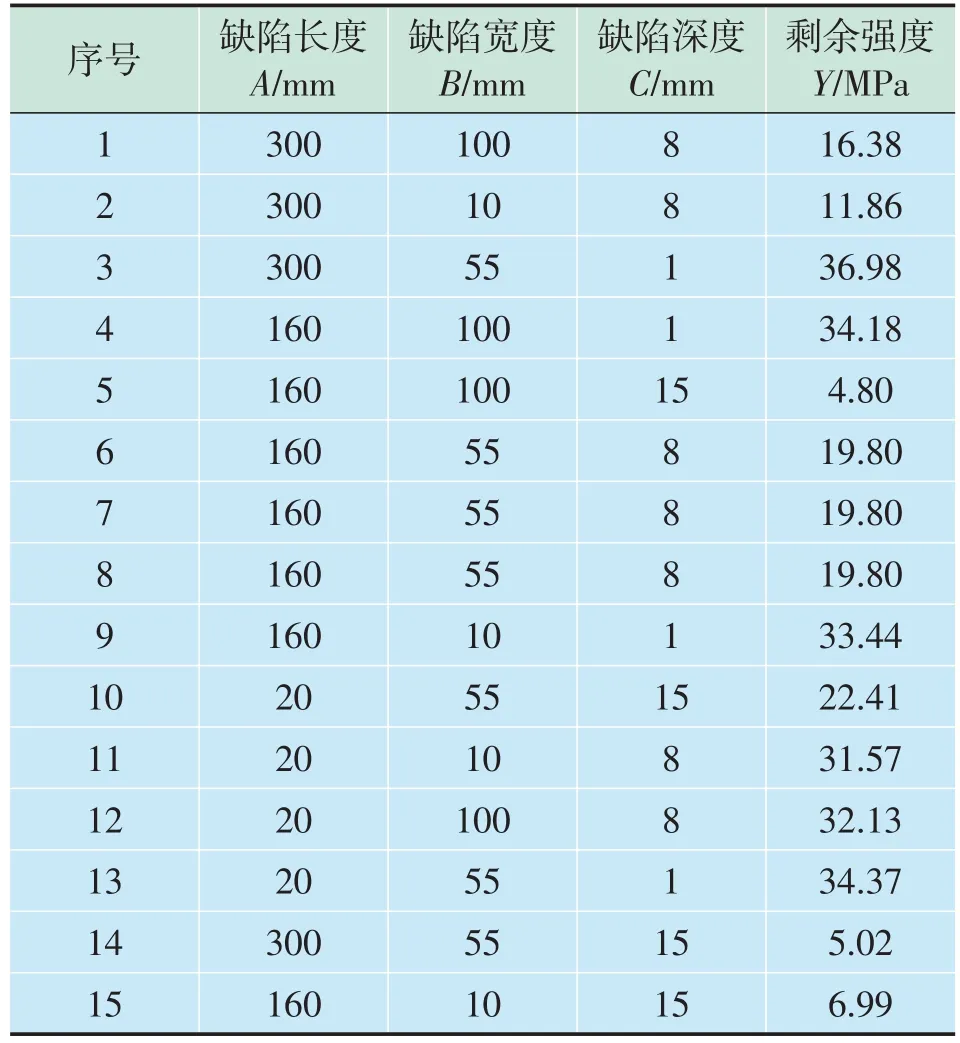
表2 实验设计及响应结果

表3对多种模型进行分析对比，可以看出，随着拟合方程阶数的不断提高，拟合系数r2也在不断提高。为了研究各因素之间的交互作用，选用二次模型进行数据拟合，该模型的r2=0.953 8，证明自变量和因变量之间的线性相关性较好，有95.38%的因变量可以由自变量来解释，只有不到5%的变异数据不能被模型解释，方程的拟合度较好；二次模型的Prob>F值小于0.05代表模型差异显著，实验的水平取值合理，实验结果不是随机出现，方程可以对样本数据进行很好的预测。由图2模型的残差正态分布可知，数据基本呈线性关系，都分布在一条直线上，说明数据的可靠性较好，可以准确地分析和预测腐蚀管道的剩余强度数值。

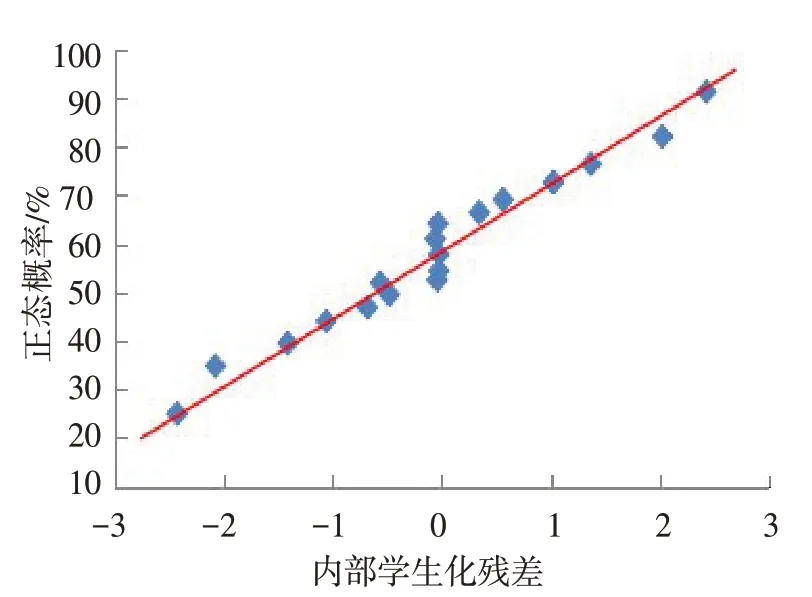
图2 二次模型的残差正态分布

表3 多种模型分析对比

根据表2的实验结果，剩余强度Y对3个自变量的二次线性拟合方程：Y=19.8-6.28A+0.45B-12.47C+0.99AB-5AC-0.73BC+4.01A2-0.83B2+0.88C2。

对二次模型的各因素进行方差分析，结果见表4。

由表4 可知，当某种因素的Prob>F值小于0.05时，代表该因素对拟合方程影响显著，缺陷长度、缺陷宽度和缺陷深度的P值分别为0.001、0.709 4、<0.000 1，说明就单因素影响分析，缺陷深度对剩余强度的影响最为显著，其次是缺陷长度和缺陷宽度；F值可以用来评估组间差异的大小，在满足P值的条件下，F值越大代表组间差异越大，影响越显著，缺陷长度和缺陷深度AC的交互因子系数F值最大为9.15，且P值为0.019 3，小于0.05，说明两者交互影响显著，而AB和BC的F值较小，P值又远大于0.05，说明之间交互影响不显著。

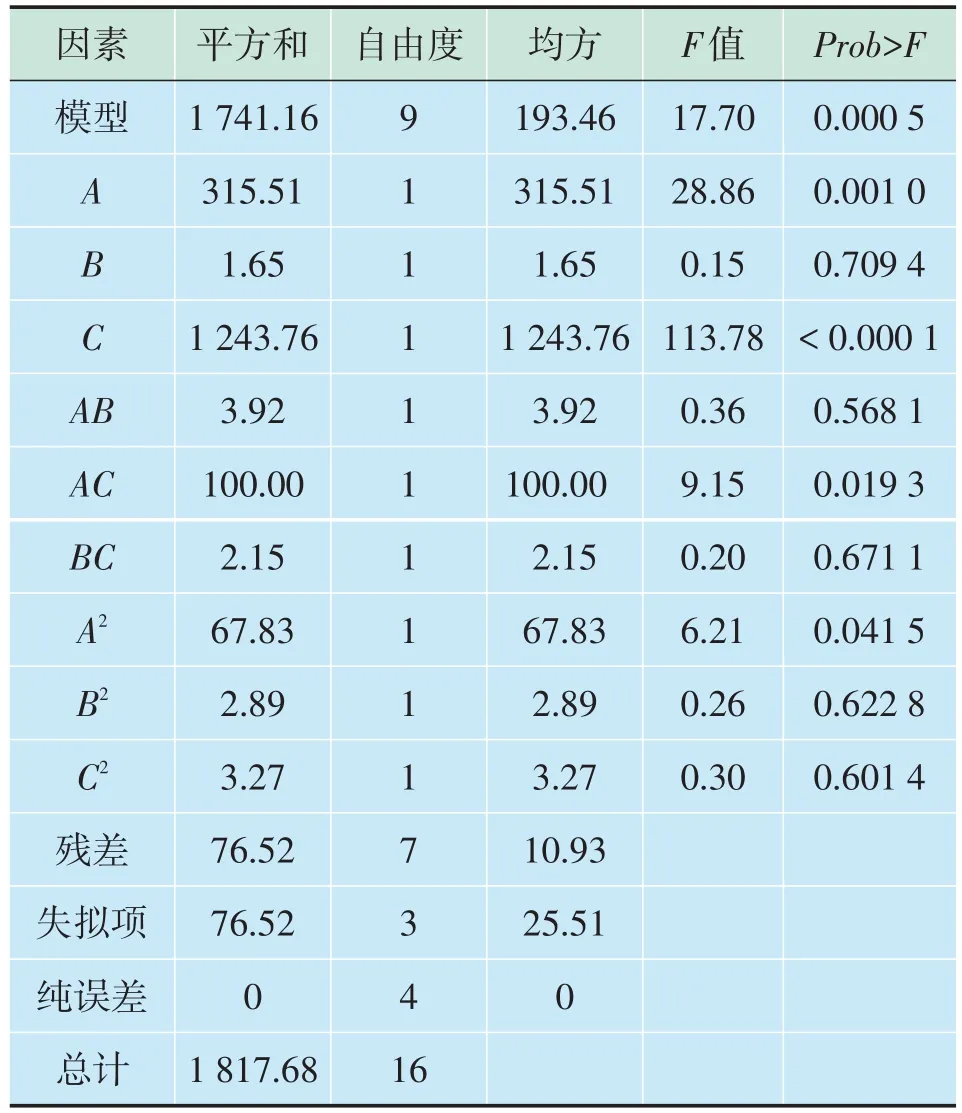
表4 二次模型方差分析

2.2 响应曲面分析

通过拟合方程的系数可知，缺陷长度和缺陷深度的系数为负值，说明两者与剩余强度之间呈反比关系，即随着长度、深度的加大，剩余强度较小；缺陷宽度的系数为正值，但该系数较小，说明与剩余强度呈微正比关系。

由于缺陷长度与缺陷深度之间的交互影响显著，因此构建了两者共同作用下的响应曲面和等高线图。由图3（a）可知，在缺陷宽度55 mm 的条件下，当缺陷长度不变的情况下，随着缺陷深度的增加，剩余强度呈倍数递减；当缺陷深度在较小的范围内波动时，随着缺陷长度的增加，剩余强度的变化趋势不大，只有在缺陷深度较大时，剩余强度才随缺陷长度的增加而大幅减少。由图3（b）可知，等高线的颜色越冷说明剩余强度越小，随着缺陷深度和缺陷长度的增加，剩余强度逐渐减小，在右上角处达到最小值。此外，等高线的弧度从30 MPa 到10 MPa 逐渐变小，从圆形向椭圆形转变，说明随着数据的增加，两者的交互作用逐渐增强；并由等高线的响应趋势可知，缺陷深度比缺陷长度对剩余强度的影响更为强烈。

图3 缺陷长度和缺陷深度的响应曲面和等高线图

3 结论

1）通过有限元分析和响应曲面相结合，构建了剩余强度的二次线性拟合方程，拟合系数为0.953 8，从方程系数中可知，缺陷长度和缺陷深度的系数为负值，说明两者与剩余强度之间呈反比关系；缺陷宽度的系数为正值，但该系数较小，说明与剩余强度呈微正比关系。

2）通过方差分析和响应曲面分析，就单因素影响而言，缺陷深度对剩余强度的影响最为显著，其次是缺陷长度和缺陷宽度；就交互因素影响而言，缺陷长度和缺陷深度的交互因子系数F值最大为9.15，且P值为0.019 3，小于0.05，说明两者交互影响显著，其余参数的交互影响不显著。

3）在实际工况中，管道的轴向夹角、缺陷数量、缺陷间距等对剩余强度的影响也很大，今后可加强这方面的研究，增强分析的全面性和客观性。