高温空气热化学物理计算模型研究
杨 光,檀妹静,聂春生,李 宇,周 禹,李潞宁,于明星,顾云军,陈其峰
(1.中国运载火箭技术研究院空间物理重点实验室,北京 100076;2.中国工程物理研究院流体物理研究所冲击波与爆轰波物理重点实验室,绵阳 621999)
1 引 言
导弹、火箭、飞船等各类飞行器在大气层内以极高的速度飞行时,飞行器周围的气体受到剧烈压缩而温度急剧升高,高温诱导的气体分子振动、转动、氧化、电荷交换、离解、电离、复合甚至多级电离等效应将对空气组分、热力学和输运性质产生重要影响[1],而空气电离形成的等离子体鞘套也可能导致通信“黒障”的出现.因此,准确地计算高温空气的热物性参数对于此类飞行器的设计有着至关重要的意义.
自20世纪50年代起至今,国外的研究者已在高温气体热力学性质研究方面进行了大量的工作[2-9],一些代表性工作如下:Drellishak等[2]计算了氩等离子体和N2-O2混合等离子体的配分函数和热力学性质,其配分函数的计算方法被广泛应用;Bacri等[3]计算了压力为1~200 atm(1atm为1个大气压)及温度为1000~30000 K范围内空气等离子体的内配分函数、组分和热力学函数;Gupta等[4]利用11组分模型讨论了空气的反应速率和热力学性质.
国内目前对于高温空气热化学模型相关的工作以应用为主,主要是基于平衡气体模型和非平衡气体模型进行了高马赫数流场和气动热环境的数值模拟[10,11],而对于高温空气热化学模型基础理论和建模工作相对开展较少,仅有少量研究工作报道.王海兴等人[12]开展了N2-O2空气12组元双温度输运性质研究,陈其峰等人[13]计算了2000~30000 K温度范围内N2-O2空气的离解、电离和热力学性质.另外,陈其峰等人也对空气主要成分氮和氧在部分离解区的热物性和离解化学反应开展了理论建模研究[14,15],对稀有气体氦、氖、氩、氪和氙在部分电离区的热物性及输运性质开展了系列性理论建模及强激波压缩实验研究[16-27],这些工作主要是针对稠密等离子体物性的研究,没有涉及高速飞行器周围空气的高温稀薄条件,其关注点与本文工作不同.
尽管国内外研究者已经对空气热物性研究了几十年,但在足够高的温度下,空气可能发生的化学反应有多少种?不同粒子的含量及其存在形式又是如何?应该用怎样的势模型描述体系中相互作用机制?到目前为止,这些问题仍然没有统一的结论,需要开展研究逐步解决.本文针对初始3组元(N2-O2-Ar)空气,建立了从初始3组元到考虑18个化学反应22组元混合体系热动力学模型以及相应的数值计算方法,对高温空气的组分浓度以及焓和比热等热力学性质进行了数值计算,对高温空气的离解电离等化学反应以及焓和热容等物性参数随温度和密度的演化规律进行了研究,并预测了飞行器高速飞行时驻点处的空气组分、压缩比、温度、热容以及比热等参数随飞行速度的变化.
2 理论模型
2.1 平衡态组分
根据标准大气模型,海平面附近空气中N2、O2、Ar的体积分数分别为78.084%、20.9476%、0.934%,三者相加大于99.9%,因此可以忽略其它组分的影响,按此体积分数比例的N2-O2-Ar空气作为计算初始条件.
在飞行器高速飞行推出强激波作用下,其周围空气主要发生高温诱导的离解、电离和复合等化学反应,这些化学反应的发生以及相应的空气组分因密度和温度差异而不同,例如,在中等温度区间(2000~6000 K),容易发生离解和复合反应,形成NO、N、O、NO2、N2O等组分;而在高温区(6000 K以上),氮氧除了离解及复合反应外,也将发生电离反应,引入分子离子(N2+,O2+)、原子离子(N+,O+)、甚至因多级电离形成的高价离子等新组分.为了尽可能反映强激波作用下高温空气粒子组分随温度及密度的变化,在局域热动平衡(LTE)和局域化学平衡(LCE)假定下,我们考虑了18个化学反应以及由此产生的22组分混合体系进行理论建模,其化学反应通道(即反应式)以及所考虑的组分见表1所列.

表1 22组分模型的化学反应通道和平衡方程Table 1 Chemical reaction channels and equilibrium equations for the 22-species model

?
表中,λ为粒子/电子热德布罗意波长,Z1(int)~Z21(int)为编号1~21组分的内配分函数.这些内配分函数由组分的内部自由度决定:对于分子和分子离子,其内配分函数的计算需要考虑电子以及振动和转动自由度的贡献;对于原子和原子离子,则只需要考虑电子部分的贡献.
以O2和O为例,其内配分函数的表达式为:

O原子内部电子激发对原子内配分函数的贡献可以表示为:

O2分子的转动配分函数可以表示为:
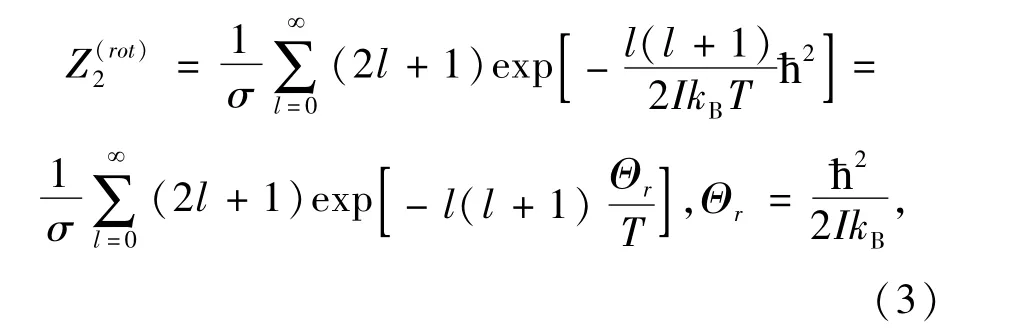
式中,Θr为转动特征温度,I为转动惯量,σ为对称数(对于同核分子,取值为2;对于异核分子,取值为1).
高温近似下(即温度T远大于Θr),可以将(3)式中的求和用积分代替,即:
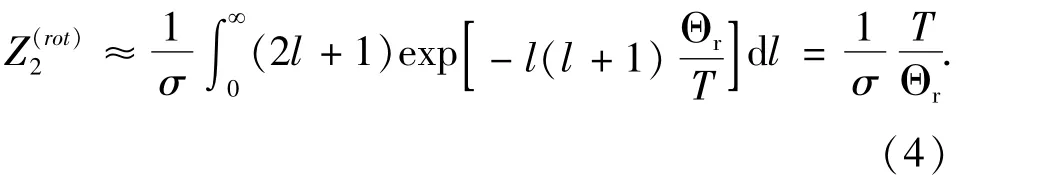
O2分子的振动配分函数,在谐振子近似下,可以通过求和得到:
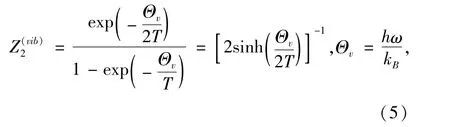
式中,Θv为振动特征温度,ω为振动圆频率(由分子势函数决定).
O2分子电子部分对内配分函数的贡献可以表示为:
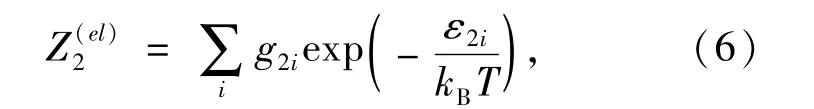
式中,ε2i为O2分子内部电子能级,g2i为对应的简并度.
对于当前所建立22组分模型,利用化学平衡条件可以得到18个离解、电离及复合平衡方程,再结合约束方程(粒子数守恒方程和电荷守恒方程),就可求解任意温度和密度状态下各组分的粒子数密度,获得平衡态下空气组分.
2.2 空气热物性模型
与配分函数的计算类似,从形式上看,可以将自由能分为原子(原子离子)和分子(分子离子)两种类型.因此,我们选择以O2+、O+为例对自由能的构建方法进行说明.
根据单组分体系自由能的形式可知,在粒子数密度、温度已知的条件下,单位质量的22组元混合体系中,O2+自由能函数的形式为:

式中,ρ为22组元混合体系的密度,可以通过各组分的粒子数密度ni和粒子质量mi给出;E3,f为O2+的形成能.
同理,单位质量的2组元混合体系中,O+自由能函数的形式为:

相比于O2+,由于缺少振动和转动自由度,O+的自由能函数得到简化.仿照以上公式,可以得出表中9种分子及分子离子(O2-、O2+、N2+、O2、N2、NO、NO+、N2O、NO2)和12种原子及原子离子(O-、O、O+、O2+、O3+、N、N+、N2+、N3+、Ar、Ar+、Ar2+)的自由能函数.对以上21种组分自由能函数求和,再加上自由电子的自由能函数,即可得出22组分体系的自由能:

我们知道,自由能函数是关于温度、体积(密度)和粒子数的特性函数.因此,从理论角度,得到体系的自由能函数以后,根据自由能的偏微分就可以得到所有的热力学函数.以下列出了主要的热力学函数(例如压力p、熵S、内能E、焓H、定容比热容CV、定压比热容Cp)与自由能之间的关系:

除了选择以温度和密度为独立变量进行建模的方法外,还可以选择以温度和压力作为独立变量建立Gibbs自由能特性函数,通过对Gibbs自由能函数做偏微分得到热力学函数.根据热力学基本理论,Gibbs自由能和Hemholtz自由能函数满足以下关系:
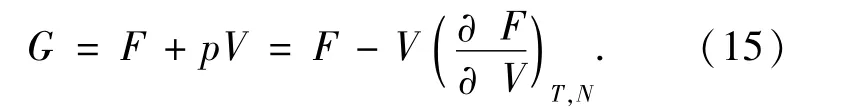
因此,在计算得到Hemholtz自由能后,利用上式即可得到Gibbs自由能函数,然后再结合热力学函数和Gibbs自由能函数之间的微分关系及麦克斯韦关系即可得到多组分体系的热力学量.
需要说明的是,当高温电离出现时,为了得到真实气体的物性参数,需要考虑带电粒子间由于Coulomb长程作用而引起的附加自由能贡献,即在总自由能中引入Debye-Hückel修正,其自由能附加项为:

在飞行器高速飞行推出强激波作用下,其驻点处的高温空气热力学状态满足Hugoniot能量约束关系:

式中,下标0和H分别代表飞行器驻点处空气在激波前和激波后的状态,激波前的状态由初始条件决定.而激波前后的状态又与飞行器的飞行速度Up相联系,其可以通过下面公式表示:

飞行器驻点处空气压缩比(ρ/ρ0=V0/VH)是激波前后的密度(或比容)之比,这样,根据方程4~12,再结合由空气初始条件确定的激波前状态,就可以得到驻点处激波后高温空气的热物性参数和空气组分随飞行器飞行速度变化关系.
3 数值结果与分析
空气组分是计算热物性的首要条件,其与高温诱导的空气离解、电离、复合等化学反应相联系.为了了解高空高速飞行器周围强激波压缩空气因温度急剧升高引起的空气化学反应及组分变化,我们给出两个典型数值模拟结果,图1和图2分别展示了以海拔高度1 km和60 km状态空气为初始条件,得到的中性粒子、分子离子、原子离子和电子浓度随温度的变化情况.从图1可以看到,对于海拔高度为1.0 km(地表附近),当温度达到约2000 K时,氧气开始离解,且在约5000 K温度时,氧原子浓度达到最大值;当温度达到3000 K时,氮气开始离解,当温度上升到约10000 K时,氮原子浓度达到最大值;当温度为6500 K左右时,氮和氧的一级电离发生,N+、O+开始出现,并且其浓度随着温度的增大而增大;当温度为约8000 K时,氩的一级电离发生,Ar+开始出现;当温度约18000 K时,氮的二级电离发生,N2+开始出现;当温度大于20000 K时,氩和氧的二级电离发生,Ar2+、O2+开始出现.由此可见,随着温度不断升高,空气离解、电离甚至多级电离等化学反应逐渐出现,新组分逐步生成,空气组分不断变化,最终形成多元混合等离子体.需要说明的是,在我们考虑的温度密度范围,O2-离子的浓度很小,基本可以忽略.O2+、N2+、NO+在较大的温度区间内均存在,但是其粒子浓度的最大值均小于1.0×10-3.从图2可以看出,海拔为60 km时,空气组分随温度的变化也表现出与海拔1 km时类似的趋势,其化学反应通道以及对应的组分也是随温度升高逐步出现的.所不同的是,相对于海拔1 km而言,海拔60 km对应更为稀薄的初始状态,空气离解电离的特征温度(即离解电离出现时所对应温度)均有所降低,氧离解特征温度降到2000 K以下,氧原子浓度在约3000 K时达到最大值;氮离解特征温度降到3000 K以下,氮原子浓度在温度6000~9000 K达到最大值并出现“平台区”;氮氧一级电离特征温度降到5000 K左右,氮离子和氧离子的浓度在15000-20000 K达到最大值并出现“平台区”;氮、氧和氩的二级电离特征温度降到15000 K左右;在温度25000 K左右,氮和氧的三级电离也出现.上述结果表明,相对于海拔1 km来说,随着海拔高度的增加,空气稀薄程度也随之增加,气体密度减小,高空稀薄空气中的各类化学反应能够在相对更低的温度下发生,也就是说,空气稀薄条件的增加有利于化学反应的发生.

图1 海拔1 km高度空气组分随温度变化Fig.1 Air components vary with temperature at altitude of�=1 km
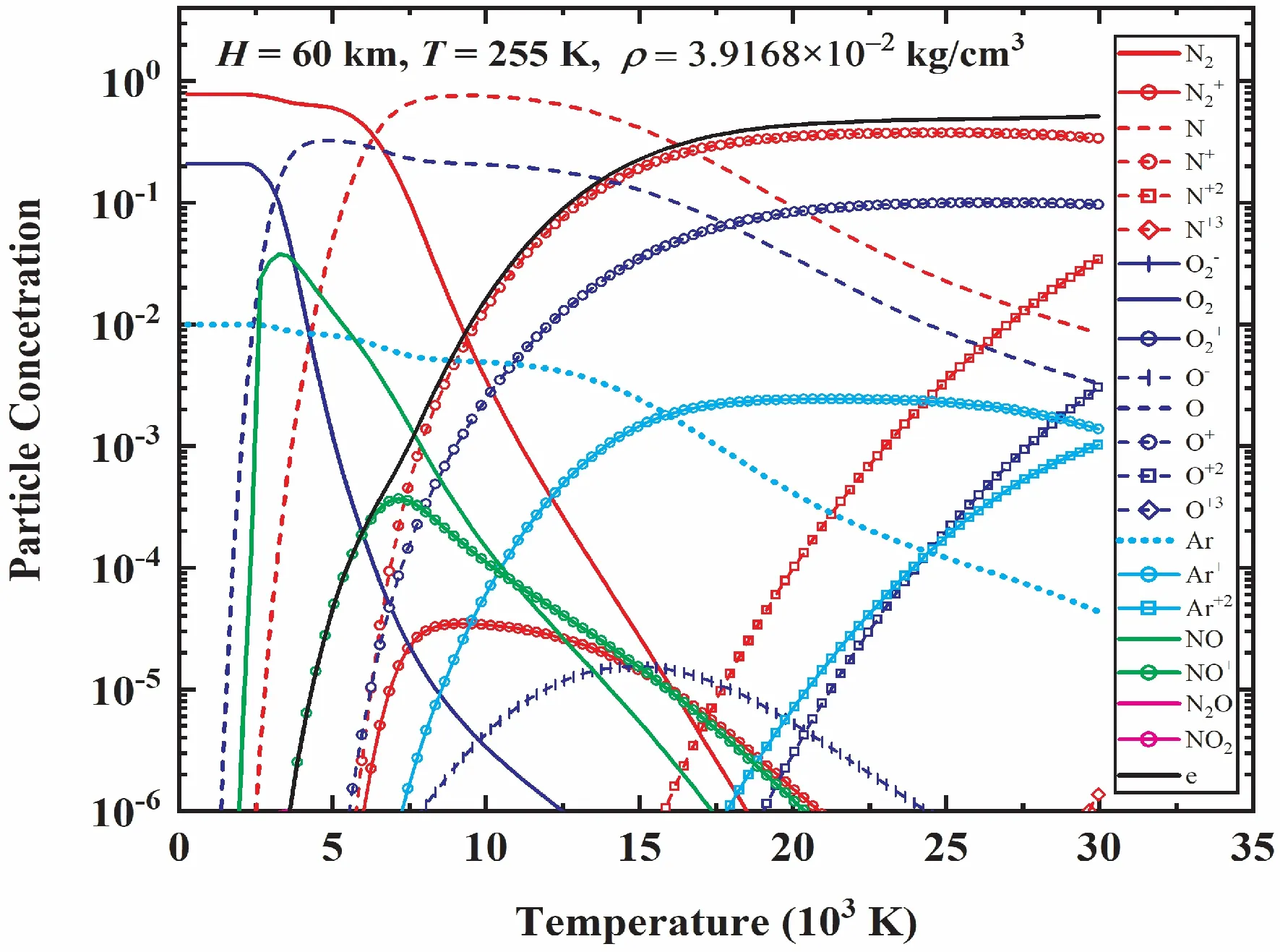
图2 海拔60 km高度空气组分随温度变化Fig.2 Air components vary with temperature at altitude of�=60 km
空气组分一旦确定,就可以根据2.2节描述的热力学量计算方法,计算空气的热物性参数,如焓、定容热容、定压热容以及比热比等.为了与现有国际流行Gupta模型比较,图3展示压力为10-4~102atm、温度为500~30000 K范围内我们模型计算的空气混合体系焓值及定压热容与Gupta等人[4]11组元模型(NASA-RP-1260,NASA是美国国家航空和宇宙航行局National Aeronautics and Space Administration的简称)计算结果的比较.可以看到,本文模型在三种不同压力下(10-4、1和100 atm)计算的焓值与NASA11组元模型所得结果较好符合,在两种不同压力下(1和100 atm)计算的定压热容也与NASA11组元模型结果基本一致.但对于压力10-4atm,本文计算的定压热容在约23000 K以上却与NASA11组元结果出现明显偏差.这种偏差出现的原因在于:10-4atm这样的极低压力有利于电离反应的发生,在23000 K以上,三级电离已经发生,而NASA11组元模型仅仅考虑到一级电离,尽管二、三级电离的出现还不足以对焓产生大的影响,但对由焓求偏导数得到的定压热容的影响却已经不能忽略.

图3 与NASA 11组分模型所得焓值与定压热容的比较Fig.3 Comparison of enthalpy and constant pressure heat capacity with NASA 11-species model
定压与定容热容是表征系统的热量交换的物理量,也在一定程度上与空气的离解电离化学反应相联系.为了研究空气稀薄程度对这两个热物性参数的影响,图4给出了我们模型计算海拔1 km和60 km高度下大气定容和定压热容随温度的变化.可以看到,这两个热容均随温度增加表现出波动变化,经分析发现,这种波动变化与空气发生离解电离等化学反应以及新组分的形成有关.对于海拔1.0 km高度,定容比热容出现的3个波峰分别对应于氧分子的离解、氮分子的离解以及氮和氧原子的一级电离,由于N+、O+浓度随温度变化趋势基本一致,因此,在定容热容上只对应一个波峰;对于海拔60 km高度,定容热容的波动变化更为剧烈,出现了四个波峰,它们分别对应于氧分子的离解、氮分子的离解、氮和氧原子的一级电离、以及氮原子的二级电离.对于定压热容来说,其随温度和海拔高度的变化表现出与定容热容相类似的变化趋势,但是相同温度下的定压热容总是大于定容热容.通过对比研究不同海拔高度稀薄空气热容变化趋势可以看出,随着海拔高度的增加,当空气越稀薄,高温热容波动变化就越剧烈,这充分反映了能量转化变化过程.

图4 不同海拔高度下定容热容与定压热容随温度的变化Fig.4 The constant volume heat capacities and constant pressure heat capacity versus temperature at different altitudes.
众所周知,比热比(定压热容与定容热容之比)能够更加细致地反映热量交换波动过程.与不考虑化学反应的理想气体不同,高温真实气体的比热比不仅是温度的函数,同时也与密度有关.为了研究不同海拔高度下比热比随温度的演化规律,图5分别给出了海拔高度1 km和60 km典型比热比随温度变化的模拟结果.可以看到,常温下,氮分子和氧分子振动自由度被冻结,平动和转动自由度完全激发,此时,比热比的值为1.40;随着温度的升高,振动自由度逐渐被激发,比热比呈现下降趋势;当温度达到约2000 K时,海拔高度为60 km和1 km处大气比热比随温度变化曲线开始分离,这是由于密度不同时,氮分子和氧分子离解特征温度和离解速率不同所导致的;当温度进一步升高时,比热比随因化学反应导致新组分的产生而不断波动变化,但是,相比于热容的波动,比热比的波动规律更加复杂.

图5 不同海拔高度下比热比随温度的变化Fig.5 The specific heat ratios versus temperature at different altitudes.
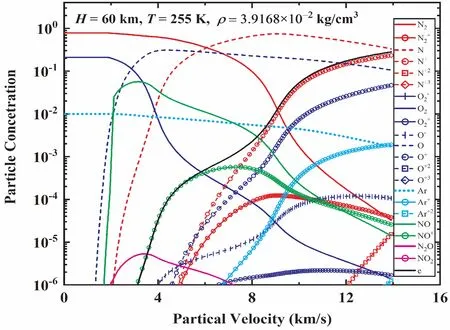
图7 60 km海拔高度下飞行器驻点处空气组分随飞行速度的变化.Fig.7 Air components at aircraft's stagnation point with flight speed at altitude of�=60 km.
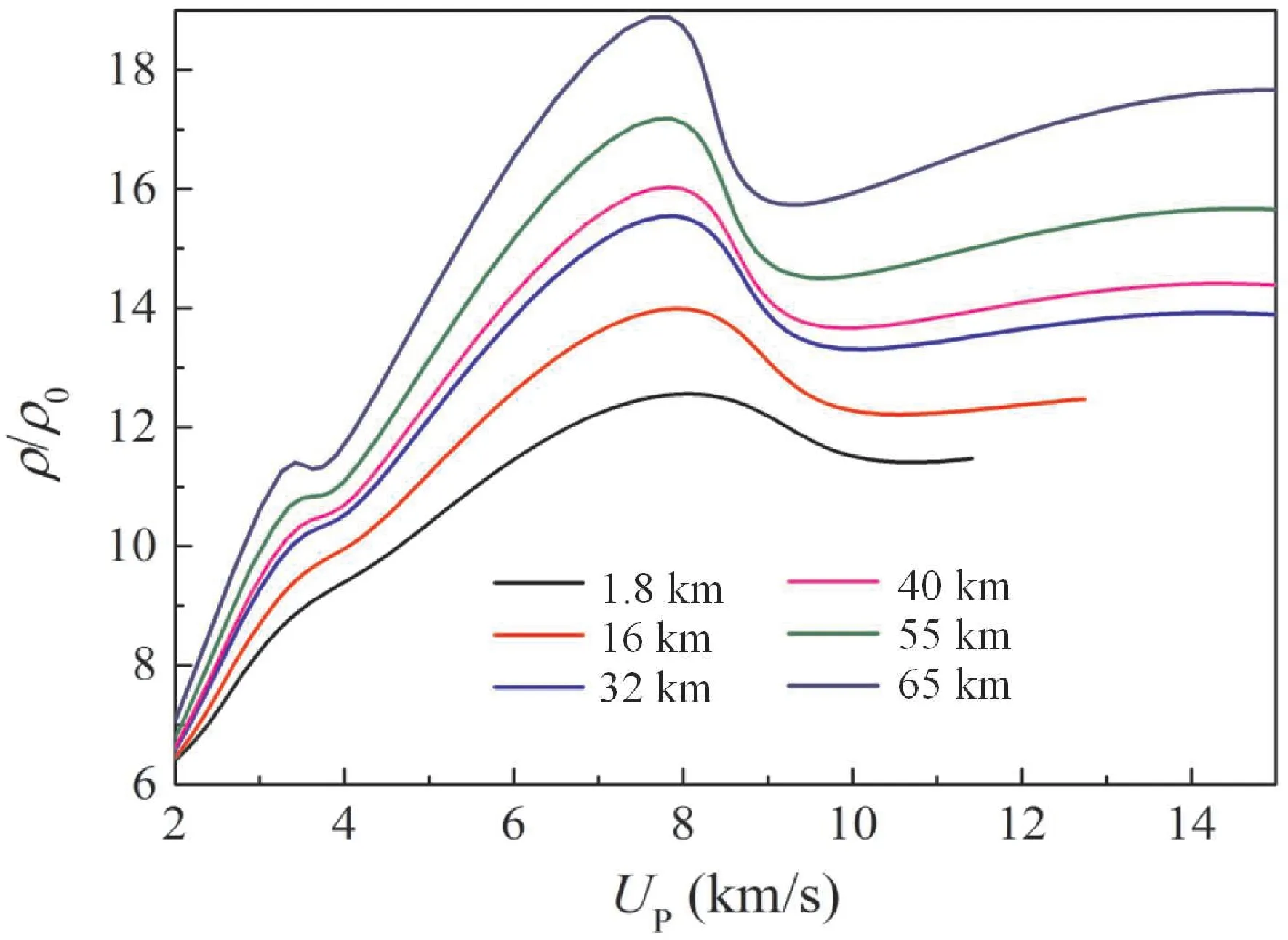
图8 不同海拔下飞行器驻点处空气密度压缩比随飞行速度的变化.Fig.8 The density compression ratios of air with flying speed at different altitudes.

图9 不同海拔下飞行器驻点处空气的温度随飞行速度的变化.Fig.9 The air temperatures at the aircraft's stagnation point with flying speed at different altitudes.
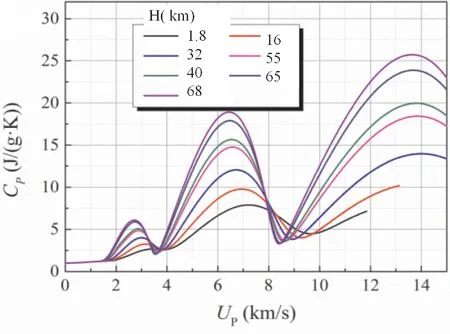
图10 不同海拔下飞行器驻点处空气定压热容随飞行速度的变化.Fig.10 The air's constant pressure heat capacities at the aircraft's stagnation point with flying speed at different altitudes.
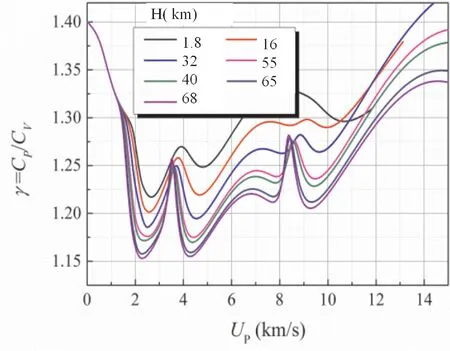
图11 不同海拔下飞行器驻点处空气比热比随飞行速度的变化Fig.11 The air's specific heat ratios at the aircraft's stagnation point with flying speed at different altitudes.
需要说明的是,上述高温空气组分及热物性参数计算主要针对等容过程,即其结果是在确定的密度条件下得到的.当飞行器高速飞行时,其将向周围空气推出激波,飞行器周围空气在激波作用下形成高温等离子体,这种高温等离子体的压力、密度和温度状态、相应的热容和比热比等参数、以及所包含的空气组分随飞行器飞行速度和所处的海拔高度而变化.其中,在激波作用区域,飞行器驻点处空气经激波作用所产生的高温等离子体热物性参数、所发生的物理化学反应以及空气组分随飞行速度的变化趋势对于工程设计具有重要的实际意义.为此,基于所建立的模型,我们对飞行器在不同海拔下(海拔高度H=1.8,16,32,40,55,65 km激波前分别对应密度ρ0=1.0,0.1,10-2,5×10-3,10-3,10-4kg/m3)飞行时其驻点处高温空气的组分、密度压缩比(ρ/ρ0)、驻点温度、热容及比热比等热物性参数随飞行速度的变化进行了预测,其结果见图6~11所示,这些预测结果不仅有助于认识高速飞行器周围高温稀薄空气因激波加热产生高温诱发的物理化学现象,也可以为飞行器热防护材料等设计提供科学依据.
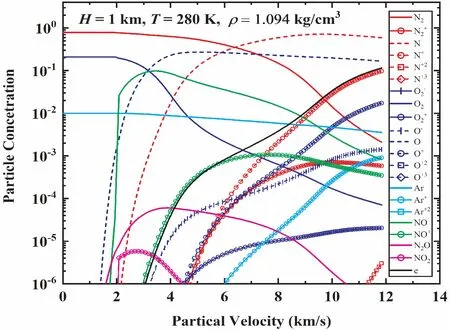
图6 1km海拔高度下飞行器驻点处空气组分随飞行速度的变化Fig.6 Air components at aircraft's stagnation point with flight speed at altitude of�=1km.
4 结 论
本文基于局域热动平衡和局域化学平衡假设,针对N2-O2-Ar空气体系,建立了考虑18种化学反应产生22组元混合体系的热化学物理计算模型,模型能够依据温度及密度的不同自适应地实现从初始3组分(N2、O2、Ar)到最多22组分(N2、N2+、O2、O2-、O2+、NO、NO+、N2O、NO2、N、N+、N2+、N3+、O、O-、O+、O2+、O3+、Ar、Ar+、Ar2+、e)高温稀薄空气组分及热物性参数的计算,其可靠性通过与国际流行多组分模型的对比得到了验证.基于该模型,研究了高温空气化学反应、组分、以及焓、热容和比热比等热物性参数随温度和海拔高度的变化趋势,分析了高温空气化学反应发生的温度条件(即反应特征温度)及其随空气稀薄程度不同的变化规律和高温引起化学反应导致的热容和比热比波动变化现象,并对飞行器高速飞行时驻点处的高温空气组分、压缩比、温度、热容以及比热比等参数随飞行速度的变化给出了预测.所取得的结果及规律性认识,有助于我们更好地认识高速飞行器周围稀薄空气因强激波压缩产生的高温诱导发生的物理化学反应、现象和作用机理,并为飞行器热防护材料等设计提供科学依据.

