三方结构MgSiO3(0001)表面的几何结构，电子结构及表面能

蒋城露，刘福生，唐 斌，刘其军，张明建

(1.西南交通大学物理科学与技术学院材料先进技术教育部重点实验室，成都 610031；2.西北工业大学凝固技术国家重点实验室，西安 710072)

1 Introduction

(Mg，Fe)SiO3is believed to be the most dominant constituent in the earth's lower mantle[1-5]，which attracts wide attention[6-11]because its equation of state(EOS)shows important information in the lower mantle.Especially，MgSiO3with perovskite and post-perovskite structures has been largely investigated，included its elasticity[1]，viscosity[6]，sound velocity[11]，thermal conductivity[12]，phase transition[13]，and equation of state[14].Though its bulk properties have been detailedly addressed，its surfaces and boundaries which play important roles in rheological and geophysical processes[15]have rarely been taken into account.Alfredsson et al.[15]studied the surface structures and energetics of orthorhombic MgSiO3，showing that the most stable surface was(001)surfaces.Furthermore，they found that the Fe2+and Ca2+doped surface structures of orthorhombic MgSiO3had lower energies compared with the pure surfaces[16].

Besides the importance of MgSiO3in earth physics，it is used as ceramics[17，18]，luminescent materials[19]and bio-compatible piezoelectric materials[20].However，to the best of our knowledge，there are poor theoretical references about the surface properties of others MgSiO3phases.Hence，ilmenite structure of trigonal MgSiO3[21，22]inspires our interests，which space group is R3-.This paper will provide predicted conclusions，which can help the future experimental works in trigonal MgSiO3.

In the paper，we have investigated the geometric structures，electronic properties and surface energies of trigonal MgSiO3(0001)surfaces as well as the bulk properties by using the density functional theory.

2 Computational methods and models

We investigated the bulk and surface properties of trigonal MgSiO3using the ultrasoft pseudopotential，the generalized gradient approximation(GGA)with Wu and Cohen functional[23]was employed as the exchange-correlation energy.All calculations were performed using the CASTEP code[24].The O 2s22p4，Mg 2s22p63s2，and Si3s23p2were treated as valence electrons.The k-point samplings were associated with Monkhorst-Pack k-point[25]in Brillouin zone，where the meshes of k-point in reciprocal space were smaller than 0.1Åto ensure the calculated precision.The meshes of bulk and surface were 3×3×2 and 3×3×1.The BFGS[26](Broyden-Fletcher-Goldfarb-Shanno)algorithm was used to ensure the convergence precision 5.0×10-6eV per atom.The cut off total energy was 380 eV.

Fig.1 shows the crystal structure and surface models oftrigonal ilmenite MgSiO3，included Mg10Si8O24，Mg8Si10O30，Mg8Si8O24surface models in different terminations.The thickness of vacuum layer in slabs is 15Åto ensure that all interactions between the slabs were negligible.Three terminations are Mg-，Mge-，and SiO3-terminated MgSiO3(0001)surface for Mg8Si8O24，Mg10Si8O24and Mg8Si10O30，respectively.Mg-terminated MgSiO3(0001)surface is a stoichiometric surface.Others are nonstoichiometric surfaces.The slabs include 40，42，and 48 atoms for Mg8Si8O24，Mg10Si8O24，and Mg8Si10O30，respectively.

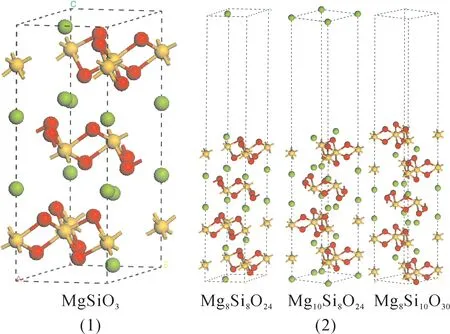
Fig.1 The bulk crystal structure(1)and the periodic surface layer(2)of MgSiO3.Where the green，yellow，and red spheres are magnesium，silicon，and oxygen，respectively.(green-Mg，yellow-Si，red-O).

3 Results and discussion

3.1 Bulk properties

Thespace group of ilmenite MgSiO3belongs to R3-.The calculated bulk lattice parameters a and c are shown in Table 1 compared with the experimental data[22].It can be seen that the calculated values are in good with experimental data.The electronic structure of bulk MgSiO3has an insulator characteristic with a direct bandgap 5.737 eV as shown in Fig.2，which is a little smaller than the experimental result[27].In Fig.3，the total density of states is composed of the orbits s and p of Mg，Si，and O atoms.It can be seen that the valence band is mainly consisted of O-p，Si-s，and Si-p.The density of states of atom Mg are in lower valence bands，where the electronic states are relatively localized.The conduction band is mainly formed with Si and Mg.The distribution of density of states shows that the Si-O bond is mostly covalent and the Mg-O bond shows ionic property.

Table 3 Calculated cleavagerelaxation Erel(X)and surface ESurf(X)energies in different terminations.

Table 3 Calculated cleavagerelaxation Erel(X)and surface ESurf(X)energies in different terminations.

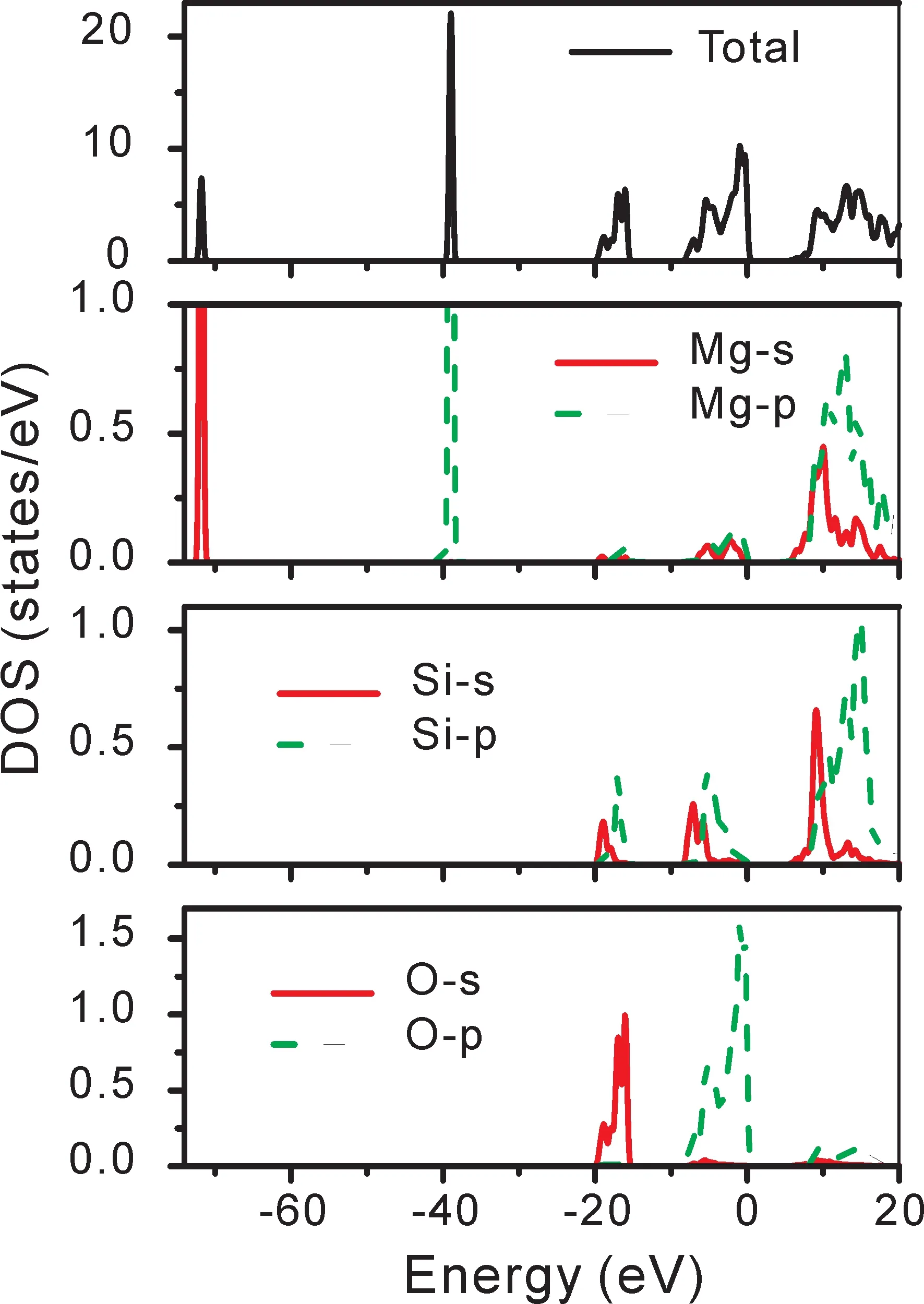
Fig.3 The density of states of ilmenite MgSiO3

Table 1 Theoptimized lattice parameters compared with experimental data.

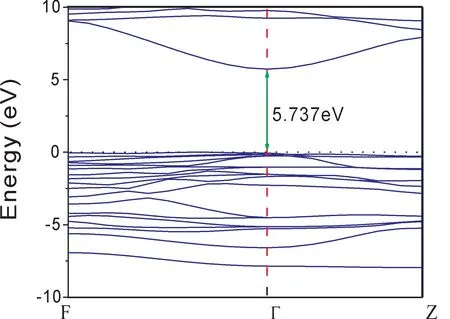
Fig.2 The electronic structure of ilmenite MgSiO3，where F(0.5，0.5，0)Z(0.5，0.5，0.5)，andΓ(0，0，0)represent different k point

3.2 Surface electronic properties

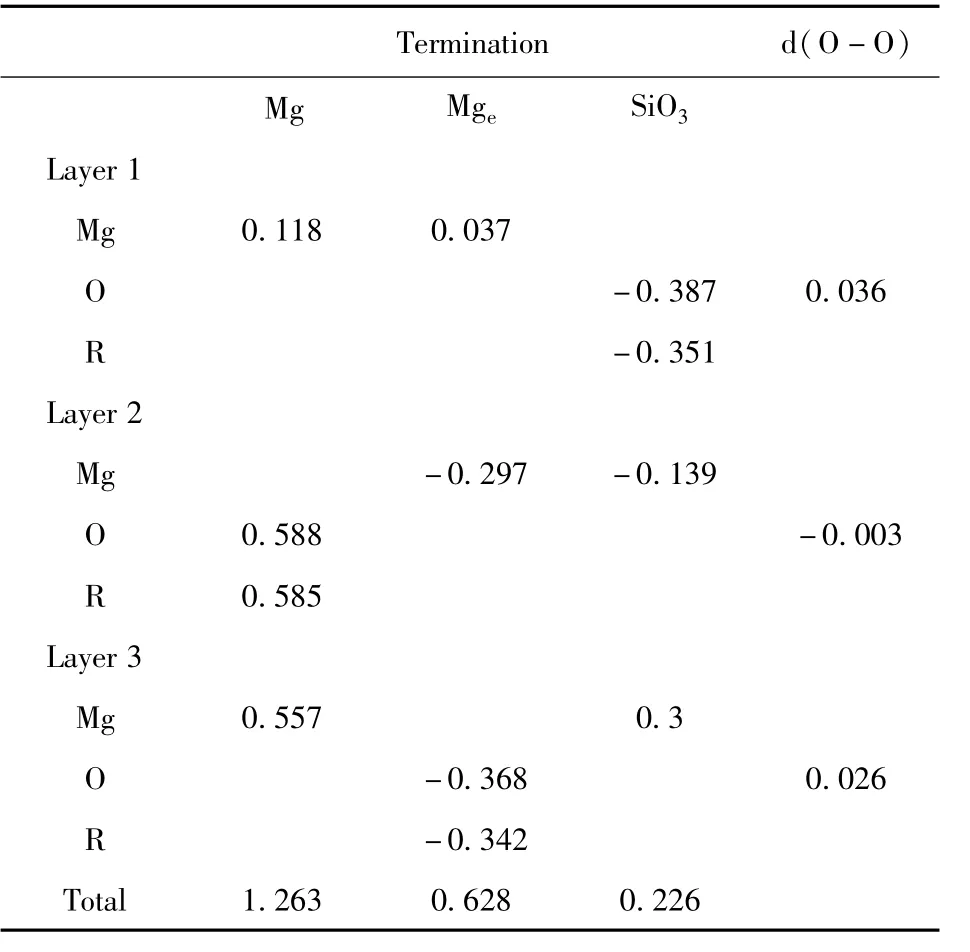
Table.2 Relaxations(Å)and Rumplings(R，Å)in different terminations along surface normal.Positive(negative)value represents the direction of outward(inward)relaxations.Where the d(O-O)is the distance of atoms O out of plane in group SiO3.

As we all known，the density of states of electrons have a great relationship with conductivity，superconductivity，masers and lasers[28].The electronic states of surface in different terminations are compared as shown in Fig.4-6.In Fig.4，all slabs have a direct bandgap，and the bandgap for electron transition is ordered 0.422 eV(Mge)<1.934 eV(SiO3)<3.839 eV(Mg)<5.737 eV(bulk).It can be seen that the termination Mgeis metallic.We find that the extra atom Mg decreases bandgap directly as shown in Fig.5 and Fig.6，which provides and accepts excitons.The bandgap of termination SiO3decreases emerged P-type conductive，where the atom Mg induces a lower conduction bond as shown in Fig.5 and Fig.6.In all，the termination SiO3presents P-type conduction，and termination Mgeis metallic.While the termination Mg retains the property of insulator.

Fig.4 The calculated electronic structures of bandgap of different slabs near fermi-level.

Fig.5 Partial and total densities of states in Mg-Si-O(0001)surface，compared with bulk.

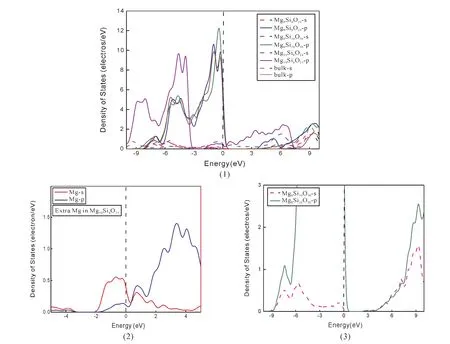
Fig.6 Partial density of states of one MgSiO3-MgSiO3 unit in Mg-Si-O(0001)surface，compared with bulk(1).Density of states of extra Mg in slab Mg10 Si8O24(2).Density of states of slab Mg8 Si10 O30(3).

As shown in Fig.7，the local potential can express the information of molecular properties and dynamic process[29].The local potential reveals that both Mg-Si and Mg-O bonds areσmodes with head-to-head.while there is no obvious bond between atoms Mg in slabs or bulk crystal，and the characteristic of Mg-Mg is ionic.Slabs have a structural relaxation compared with stable bulk crystal.It can be seen that the slabs have a bigger local potential，where the relaxation process would produce a bigger local potential stored in surface.In conclusion，the layers have a bigger potential bonds compared to bulk crystal，because the strong bonds are needed for layered stability.

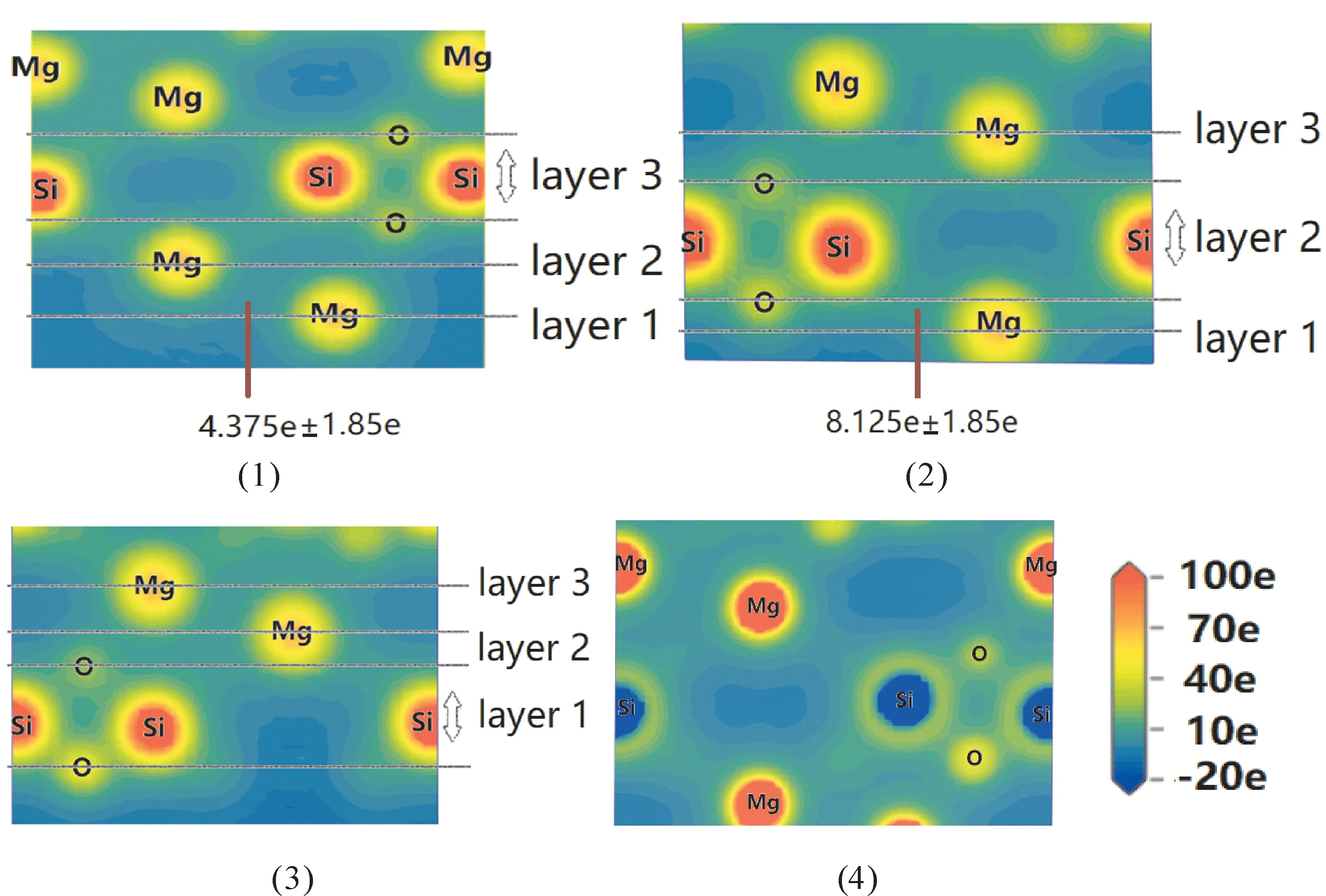
Fig.7 Calculated local potentials for Mg10 Si8 O24(1)，Mg8 Si8 O10(2)，Mg8 Si10 O30(3)，bulk(4)，where the choices of layers are the same as structural relaxation.

3.3 Surface energies

In the previous report，surface energies have decided the stability of slabs[29，30]，the surface energies of different terminations Esurfare described by two methods[31-33].We note that terminated Mgeand SiO3surfaces are complementary and the termination Mg is stoichiometric termination.So，the average surface energy of three modes is listed as follow[31，33]：

where the relaxation energiesandare terminations Mge，Mg，and SiO3，respectively.Srelrepresents 2D area of cell.n is total number of bulk formula.

Another methodreferred to surface energy ESurf，which is the sum of the cleavage energy and the relaxation energy[32，33]：

The calculated cleavage，relaxation and surface energies of three terminations are shown in Table 3，the surface energy ESurf0.41 J/m2shows that the termination-X is metastable.The positive cleavage energyis because the process of cleavage is endothermal.The negative Erel(X)is because the relaxed process is exothermic.The surface energies of different terminations are calculated in second method，compared with previous report.The cleavage energies 0.84 J/m2and 0.62 J/m2in(0001)plane compared with reference 0.93 J/m2[34]prove that our results are reasonable.The surface energy can express the thermodynamic stability[32，33]，and the order is Mg(0.06)>SiO3(0.34)>Mge(0.83).

MgSiO3is a ternary oxide，the chemical potential uMgSiO3of trigonal ilmenite structure is expressed[32，34]：

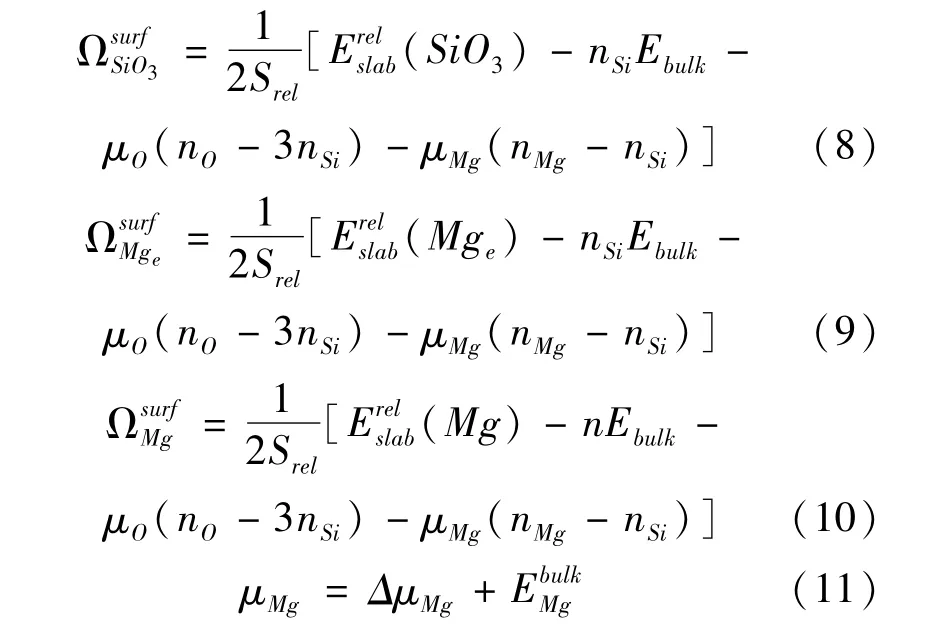
The variable ofμSiis estimated by surface grand potential：Surface grand potentialΩpresents the stability of the surface in different content Mg.The(nMg-nSi)represents the excess(if positive)or the deficiency(if negative)number of atom Mg in the terminations.Small value of△μMgpresents Mg-poor conditions，big value represents Mg-rich conditions opposite.It shows that the termination Mgeis most stable with the increase of△μMgas shown in Fig.8.And the termination SiO3is most unstable.It is predicted that the termination Mgeis most probably to be observed in surface MgSiO3where the condition is Mg-rich.The order of surface grand potentialΩ is Mge>Mg>SiO3with the variation of △μMg.

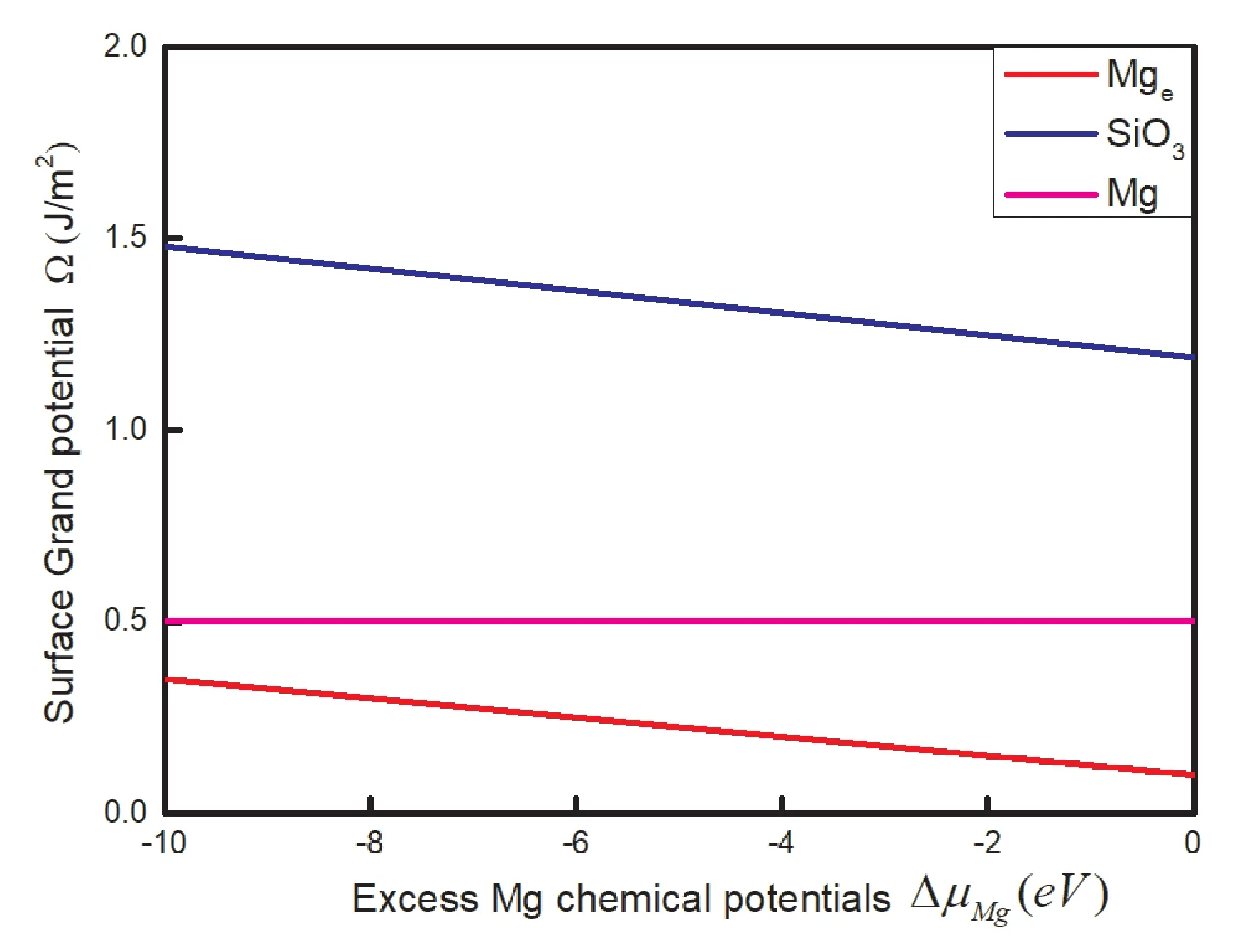
Fig.8 Stability diagram of the MgSiO3(0001)surface with the increase of chemical potentials Mg.

4 Conclusions

The density functional theory is employed to investigate the basic physical properties referred to geometric structures，electronic properties and surface energies of trigonal MgSiO3surfaces(0001).And the main conclusions are listed as follow：

(1)The group SiO3has a strong covalent bonds in slabs，and atom Mg shows its ionic properties.

(2)The atomic displacement after relaxation shows the order is Mg(1.263Å)>Mge(0.628Å)>SiO3(0.226Å).

(3)The order of bandgap is 0.422 eV(Mge)<1.934 eV(SiO3)<3.839 eV(Mg)<5.737 eV(bulk).The extra atom Mg would like to provide and accept excitons.Termination Mgeis metallic，termination SiO3is P-type conductive，and termination Mg is insulated

(4)The stability from surface energy is ordered Mg(0.06 J/m2)>SiO3(0.34 J/m2)>Mge(0.83 J/m2)directly.In Mg-rich condition，the grand potential is ordered as Mge>Mg>SiO3with the variation of△μMg，where termination Mgehas a lowest grand potential.