无刷直流电机的模糊自整定MRPID转速控制方法研究

唐 伟 王立忠 庄 健 王庭凯

西安交通大学机械制造系统工程国家重点实验室，西安，710049

0 引言

无刷直流电机(brushless DC motor, BLDCM)因具有扭矩大、结构紧凑、功率密度高等优点，在军事、航空航天、工业产品、精密机床、医疗器械、汽车、家用电器和办公自动化等领域中应用广泛[1-3]。传统PID控制、模型参考自适应控制[4]、滑模控制[5]、模糊自调节控制[6]等依赖系统模型，同时面对干扰和高频噪声时表现不尽如人意。小波变换目前已广泛用于电机建模、分析和控制[7-9]，实现了信号去噪[10]和BLDCM转速的估算[11]。PARVEZ等[12]和KHAN等[13]先后提出并实现了用于电机转速控制的小波多分辨PID(multi-resolution PID,MRPID)控制器。然而，以上研究仅对MRPID控制器进行调速性能验证，没有具体分析MRPID控制器同时处理高、低频信号时的表现，并且MRPID控制器参数不具备自适应性，因此一些研究者[14-15]将小波变换与神经网络相结合，但网络训练、网络结构层数较复杂、运算量大[16]。模糊控制算法结构简单，适用于复杂、非线性系统控制。本文提出无刷直流电机转速的模糊自整定MRPID控制方法，分析验证MRPID同时处理高、低频信号的优势，同时利用模糊控制实现MRPID控制器的参数自整定，通过仿真和对比实验验证所提控制器的性能。

1 BLDCM动力学分析及MRPID控制原理

1.1 BLDCM动力学分析

本文提出的控制算法用于BLDCM的转速控制。BLDCM具有梯形分布磁通和反电动势，所使用的永磁材料的磁导率通常与空气相近，可认为电机的等效气隙长度为常数。在假设电机磁路非饱和、不计涡流与磁滞损耗的条件下，电压回路方程如下：

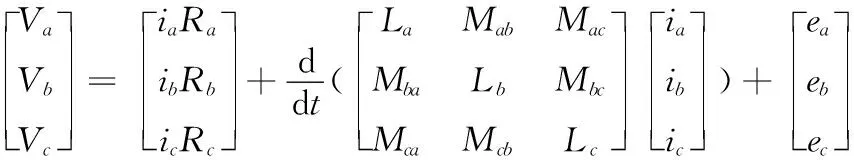
(1)

式中，Va、Vb、Vc为三相绕组相电压；ia、ib、ic为三相绕组相电流；ea、eb、ec为三相绕组相反电动势。

三相定子绕组Y型对称连接，无中线，设定子绕组的自感La=Lb=Lc=Lδ，相电阻Ra=Rb=Rc=Rδ，绕组间互感为Mξ，有

ia+ib+ic=0

(2)

式(1)可整理为

(3)

由上式可得BLDCM的等效电路模型，如图1所示。其中，VΩ为直流母线电压，P为电机三相绕组中点。三相无刷直流电机的电磁转矩

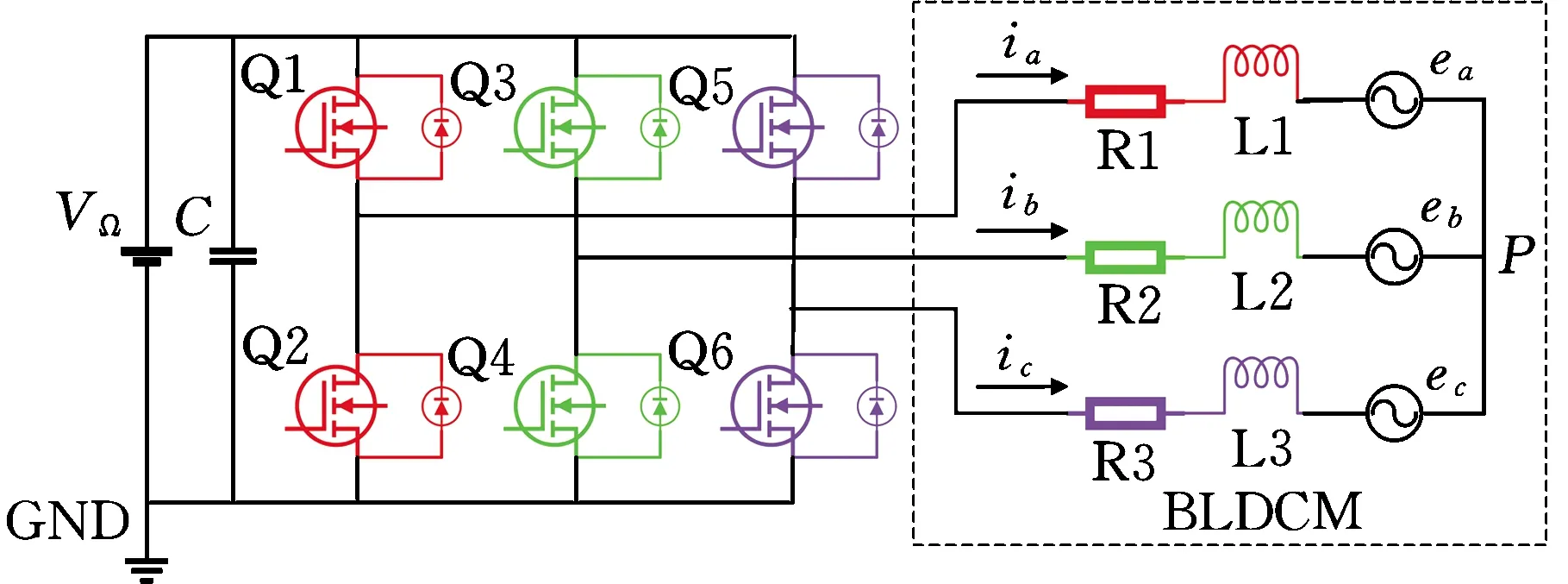
图1 三相BLDCM等效电路模型

(4)

式中，ωM为角速度。

电机运动方程为

(5)

式中，JM为无刷直流电机的转动惯量；TL为负载转矩。

1.2 MRPID控制原理

在实际应用中，传感器噪声多为高频[17]，而指令和干扰往往为低频信号，同时减少这些不确定性因素的影响十分困难，而MRPID在该条件下展现了良好的性能，主要原因在于多分辨分析[18](multi-resolution analysis，MRA)将信号分解为平滑的趋势分量和精细的细节分量。信号f(t)的离散小波变换表达式为

(6)

(7)

(8)

其中，φ*(t)、ψ*(t)分别为小波函数φ(t)和尺度函数ψ(t)的共轭函数。一个典型的2阶离散小波分解和重组的过程如下：原始样本信号f(k)经过低通滤波和高通滤波后进行抽2采样，得到趋势系数cj-1,k和细节系数dj-1,k，将cj-1,k和dj-1,k再进一步分解得到新的趋势系数cj-2,k和细节系数dj-2,k；对所得系数上采样，并与相应重组滤波器卷积运算，可得到趋势信号、细节信号和中间分辨率信号。本文的研究目标是对电机转速偏差进行小波分解，对所采集的数据应用最小描述长度准则(minimum description length，MDL)来选取最优小波基函数，MDL准则表达式如下：

(9)

滤波器长度过大会导致运算时间长，反之会引入伪迹[18]。

MRPID的基本原理[12]是通过MRA将速度偏差信号u分解N层后得到趋势分量ecj和细节分量edj,按各自增益kcj和kdj进行缩放，即

(10)

以db4小波作为小波基函数进行两层分解，根据式(6)～式(8)，可得到趋势系数ec2和2个细节系数ed1和ed2,控制原理如图2所示。控制量为

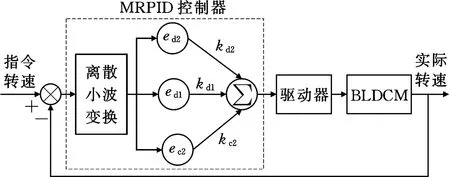
图2 两层分解MRPID控制原理

u=kd1ed1+kd2ed2+kc2ec2

(11)

为了直观体现MRPID控制方法的特点，以正弦信号u=sin(2πt)为指令信号，加入高频白噪声组成含噪输入信号，如图3所示。

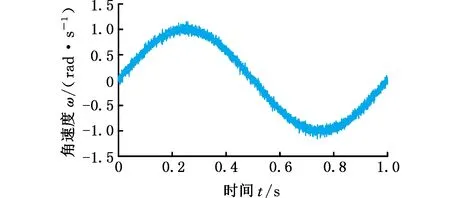
图3 含噪正弦信号

以db4小波基函数对含噪信号进行两层MRA分解，得到趋势分量el2和细节分量eh1、eh2如图4所示。可以发现：小波多分辨分解得到的高频分量能很好地提取出偏差信号中的噪声和高频失真，呈现出白噪声状态；而低频分量相较于含噪信号光滑得多，包含信号更多的原始信息。适当增大低频信号分量的系数kcN可以提高控制带宽，增大系统阻尼，从而提高系统抗干扰能力和瞬态响应；同时调整高频信号分量增益kdN使之接近0，可以获得相对平滑的控制信号并大大降低噪声对输出造成的干扰。在实际控制中，平滑的控制输出可提升被控对象的使用寿命，从而提升整个被控对象的性能。

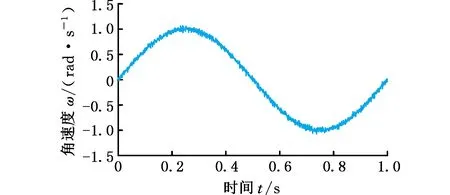
(a)el2曲线

分别以阶跃信号和人为加入白噪声后的信号作为输入，与传统PID控制器进行对比，得到电机转速在两种控制方法下受噪声的影响情况，如图5所示。可以看出，加入白噪声以后，传统PID控制方法下输出转速有明显波动，而MRPID控制方法下输出转速较为平滑稳定，这是由于MRPID中高频参数设置为0即可将输入信号的绝大部分高频噪声滤除掉。相比传统PID控制算法，MRPID控制算法表现出更好的抗高频噪声能力。

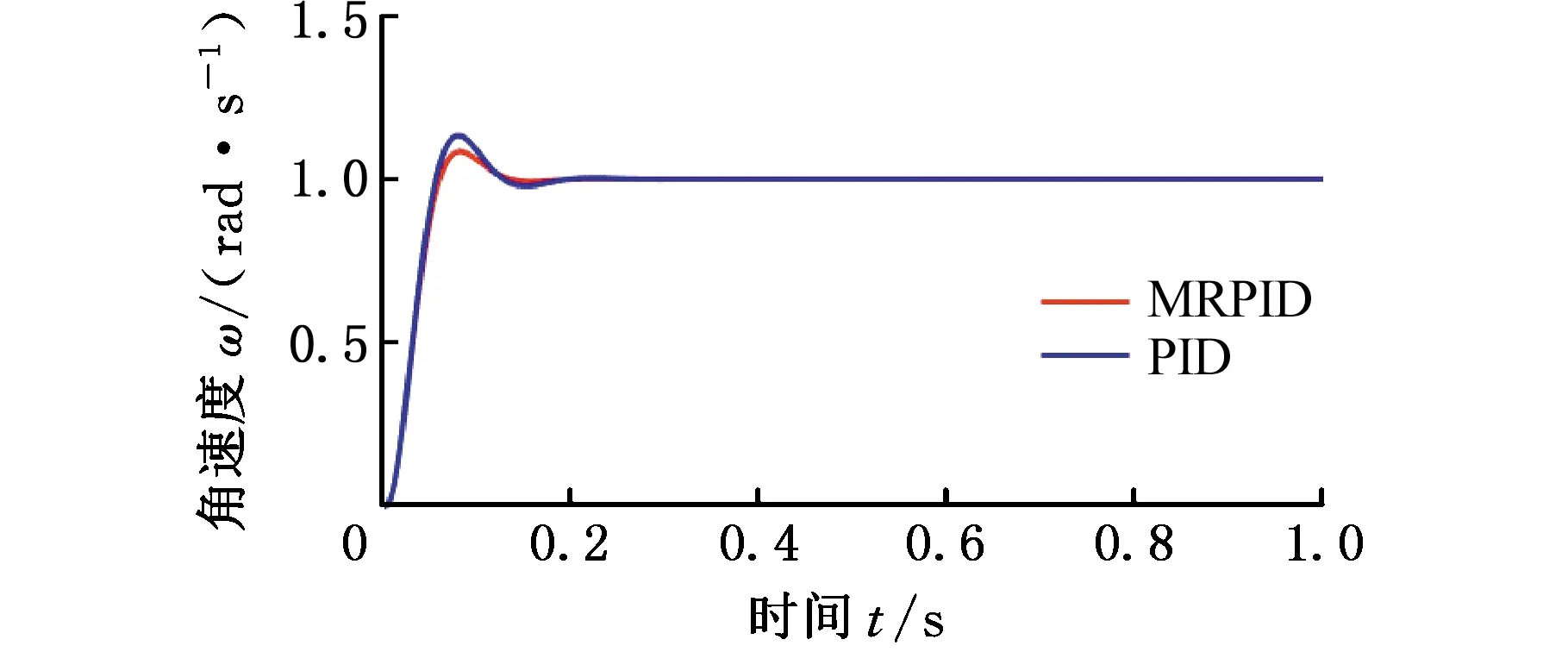
(a)无噪情况下

2 模糊自整定MRPID控制器设计

MRPID控制器可以滤除高频噪声，同时通过提高低频分量的系数实现鲁棒控制，但参数kd1、kd2、kc2仍然需要根据系统运行情况和误差分析进行优化调整，因此，采用模糊自适应算法对参数进行在线整定，以获得最优控制性能。模糊控制系统主要由模糊化接口、模糊数据和规则库、模糊推理机制以及解模糊化接口组成，结构如图6所示。

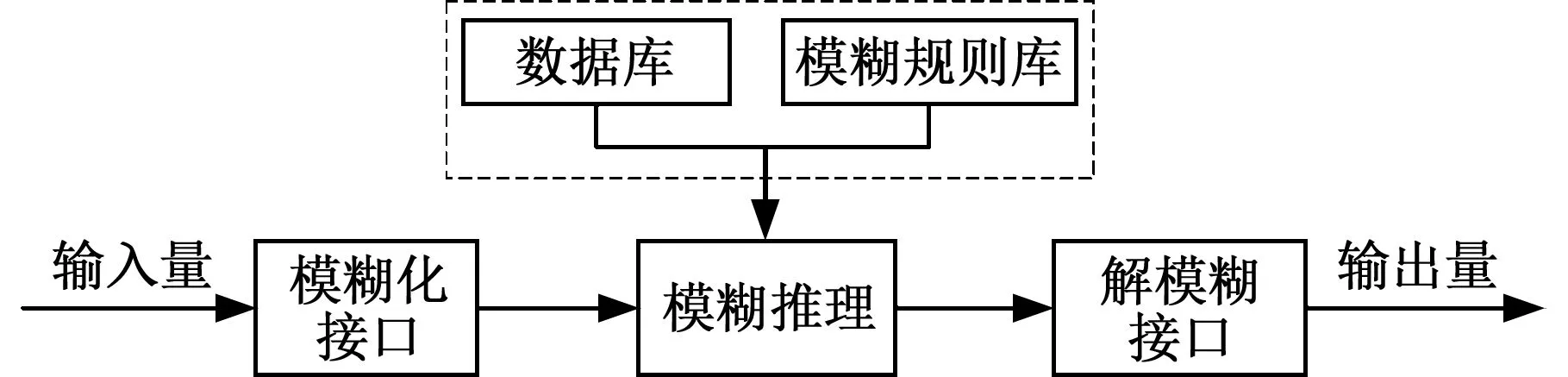
图6 模糊控制器结构

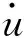
(12)

模糊子集为{NB,NS,ZE,PS,PB}，子集中各元素分别代表负大，负小，零，正小，正大。将基本论域范围内连续变化的量分级离散化，然后进行模糊处理。取值范围[a,b]可通过线性转换公式转换到[-4,4]之间，即

(13)

选择运算简单的三角形隶属函数，如图7所示。

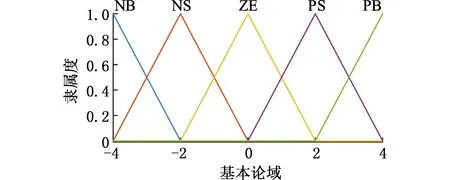
图隶属度函数

(1)当BLDCM启动或停止运行时，转速偏差较大，为加快响应速度，应取较大的kc2；为避免由于开始时转速偏差瞬时变大导致控制作用超出许可范围，kd1取适中值；同时为了避免转速出现较大的超调，通常令kd2=0。

(2)当BLDCM正常运转后，转速偏差较小和变化率处于中等大小时，kc2应当取较小值以获得较小的超调量；kd1取较小值可保证系统响应速度，同时kd2取较小值。

(3)当BLDCM转速基本恒定时，此时转速偏差较小，为使系统稳定性较好，应当取较大的kc2和kd2，同时考虑系统的抗干扰能力，取kd1=0。

根据以上分析可指定模糊推理规则，见表1。

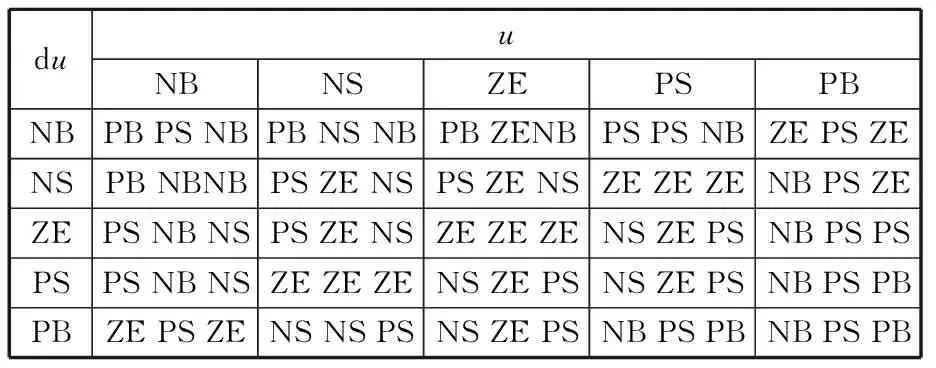
表1 kc2、kd1kd2模糊推理规则

将模糊推理的结果即模糊控制器的输出变量按重心法进行解模糊：

(14)

对于具有m个输出量化级数的离散论域情况，则有

(15)

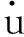
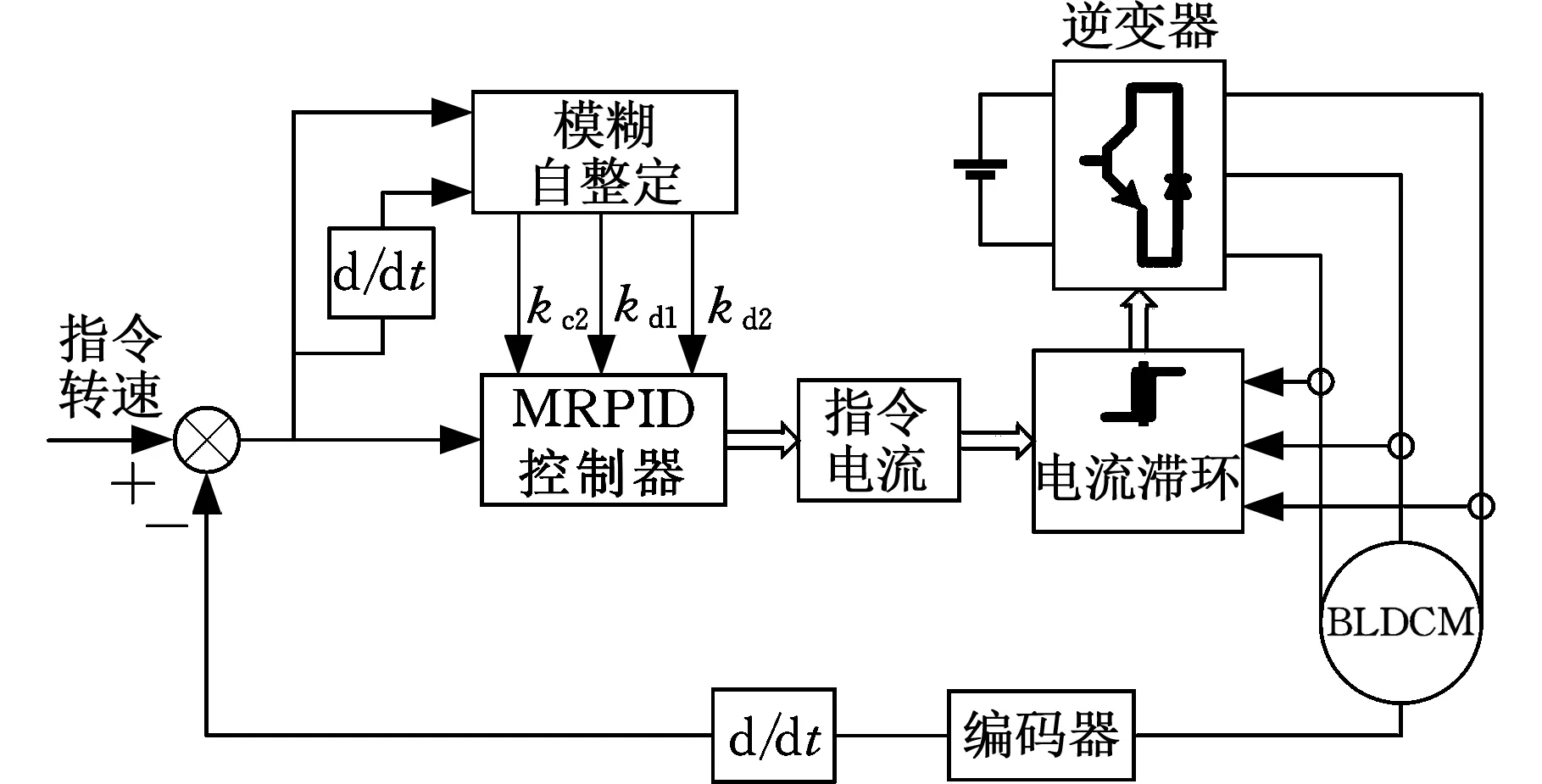
图8 模糊自整定MRPID控制系统框图

3 仿真和实验

为验证模糊自整定MRPID控制器对BLDCM转速控制的特性，进行不同工况下的仿真和实验，电流环采用PI闭环控制，速度环采用模糊自整定MRPID控制。同时以模糊PID控制作为对比，验证模糊自整定MRPID控制方法的优势。以超调量σ和稳态时间t作为控制器性能评价指标，设定转速波动范围在±0.5%内为稳态转速，到达稳态转速所需时间设为稳态时间。

3.1 仿真及分析

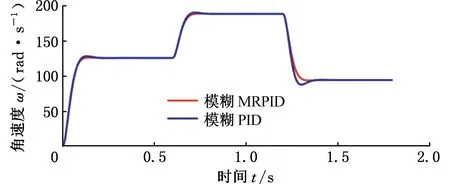
图9a所示为使用模糊PID控制器和模糊自整定MRPID控制器的BLDCM在指令速度突变情况下的Simulink仿真响应曲线，初始指令速度为251.3 rad/s(2400 r/min),在0.6 s处指令速度突变为377 rad/s(3600 r/min)，在1.2 s处指令速度突变为188.5 rad/s(1800 r/min)。图9b所示为含白噪声指令信号下的仿真结果。

(a)无噪情况下

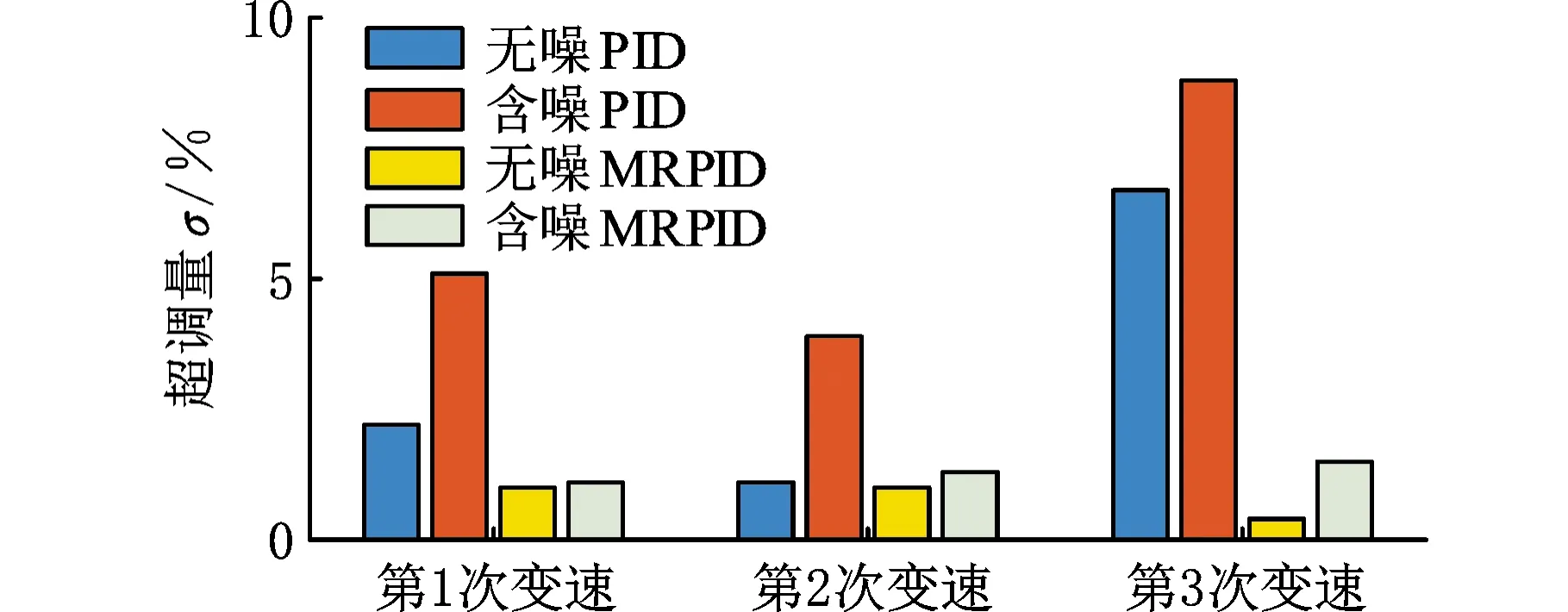
如图10所示，在不含高频噪声的理想条件下，使用模糊PID和模糊MRPID控制方法调速性能几乎相近，其中模糊MRPID超调量更小，体现了其响应快超调小的特点。在稳态转速下，模糊PID由高频噪声引起转速波动，而MRPID滤去了高频噪声，并对中低频信号进行加权重组，转速平稳，体现了MRPID的特点。由仿真结果可以看出，模糊自整定MRPID控制器相较于模糊PID控制器具有更好的速度跟随表现。

(a)超调量

图11所示分别为使用模糊PID控制器和模糊自整定MRPID控制器抗干扰仿真结果。BLDCM以指令速度314.2 rad/s(3000 r/min)运转，在0.6 s时加入扰动转矩0.1 N·m。

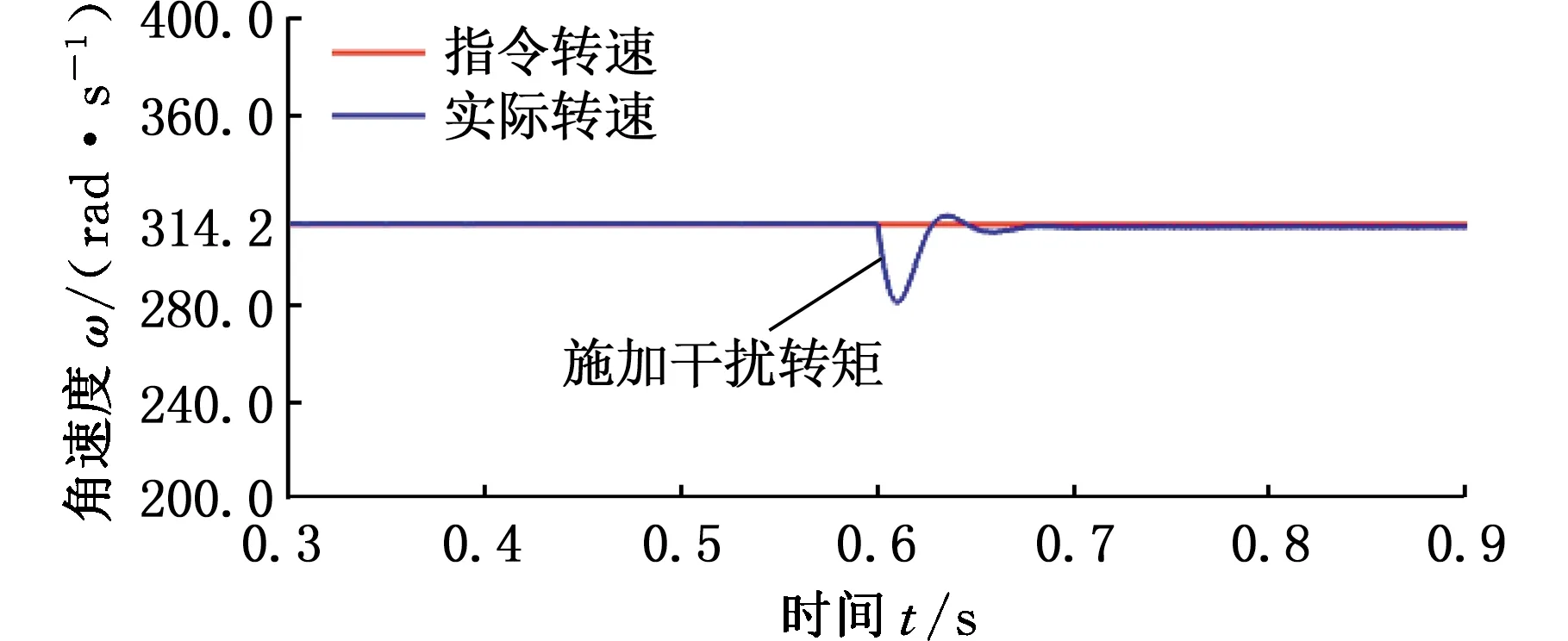
(a)干扰下模糊PID速度仿真曲线

使用模糊PID控制器和模糊MRPID控制器在干扰转矩下的表现如下：最大速度波动率分别为10.3%和6.3%，重新达到稳态速度所需时间分别为0.069 s和0.053 s，可见模糊MRPID控制器受扰动更小，具有更好的鲁棒性。

3.2 实验及分析

系统实验平台如图12所示，滞环电流控制器通过比较指令电流与实际母线电流，产生逻辑信号作为逆变器开关脉冲触发信号。实验所用电机规格参数见表2，模糊MRPID控制器中三个分量参数的初始值分别为3.5，1.1，0。

图12 BLDCM转速控制实验平台

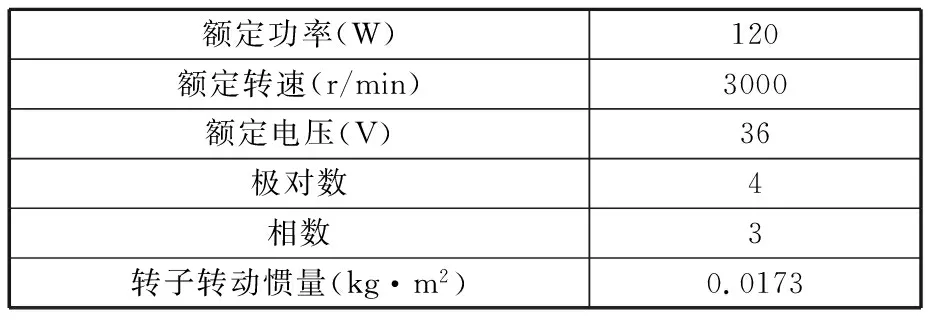
表2 无刷直流电机规格参数

指令速度突变时，使用模糊PID和模糊MRPID控制器的响应如图13所示。此过程中各分量参数变化曲线见图14。由实验结果可以看出，实验指令速度初始值为251.3 rad/s(2400 r/min),8 s处指令速度突变为377 rad/s(3600 r/min)，14 s处指令速度突变为188.5 rad/s(1800 r/min)，结果基本与仿真结果一致，体现了模糊MRPID控制方法良好的速度跟随性能。

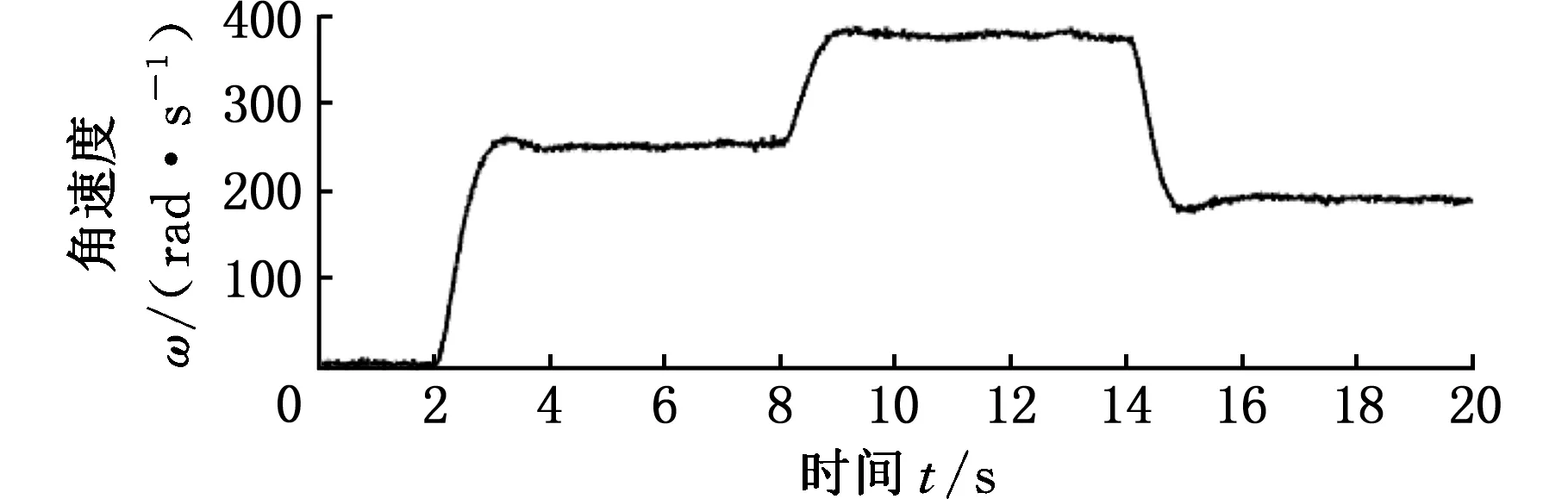
(a)模糊PID速度跟随实验曲线

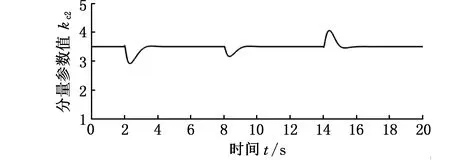
(a)参数kc2变化曲线

图15为实验中无刷直流电机转速在指令信号为时变复合信号时转速跟踪实验结果图，指令信号为(251.3+30sin(0.5πt))rad/s。使用模糊自整定MRPID和模糊PID控制均能较好地跟踪时变复合信号，但模糊自整定MRPID控制方法在动态过程中具有更小的超调量，体现了模糊自整定MRPID控制器良好的控制效果和较强的鲁棒性。

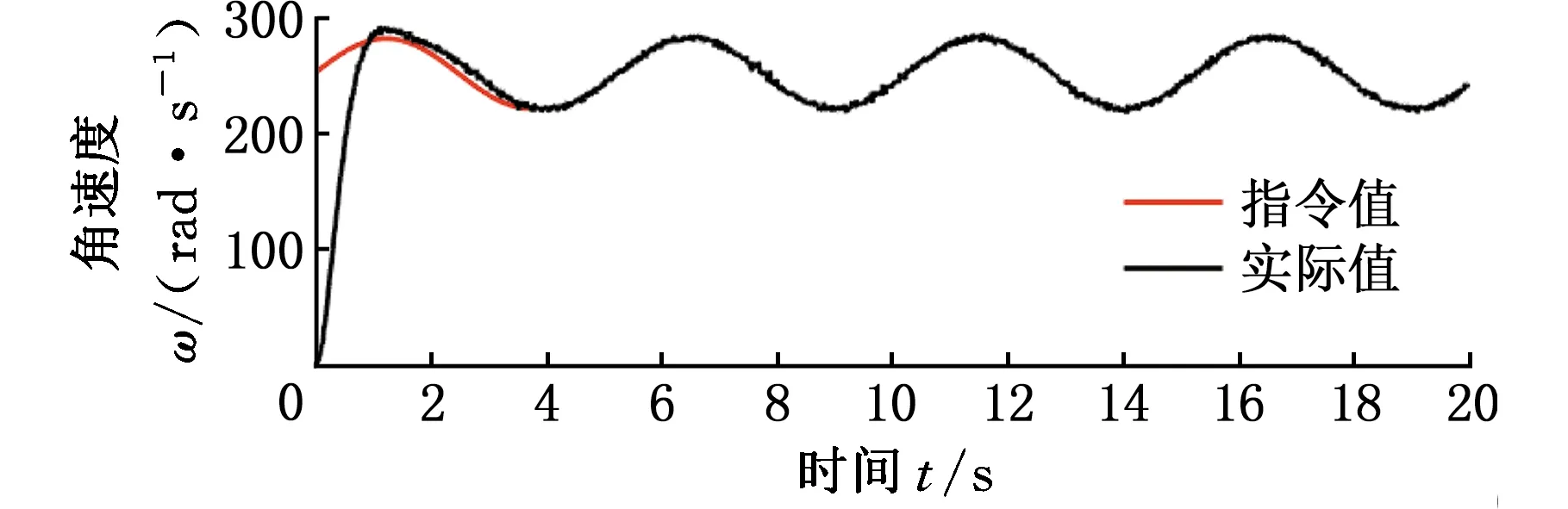
(a)模糊PID控制器跟踪时变复合信号

实验BLDCM速度为314.2 rad/s(3000 r/min)并在4 s时加入扰动转矩，分别使用模糊PID控制器和模糊自整定MRPID控制器的实验速度如图16所示，结果基本与仿真结果一致，使用模糊自整定MRPID控制下的速度波动量减小了4%，且重新达到稳态转速的时间比传统PID控制时间缩短了27%，说明模糊自整定MRPID控制器鲁棒性更好。

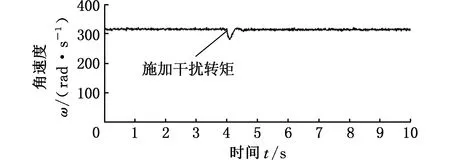
(a)干扰下模糊PID控制速度曲线

4 结论

本文提出了一种模糊自整定MRPID控制方法，用于无刷直流电机的转速控制。在MRPID控制器中，采用多分辨分析法将实际速度和命令速度之间的偏差分解为不同尺度下的不同频率分量，通过加权重组各分量来输出控制信号；利用模糊控制对MRPID控制器参数进行在线整定，以获得最优控制。本文建立了无刷直流电机的数学模型，分析了MRPID同时处理高、低频信号的优势特点，搭建了无刷直流电机转速控制实验平台。以模糊PID控制器作为对比，在不同工况下进行仿真和实验，验证所提出的模糊自整定MRPID控制器的性能。仿真和实验结果表明，所提出的模糊自整定MRPID控制器具有滤除高频噪声并且响应快、抗干扰能力强的特点，实现了对无刷直流电机转速的鲁棒控制。