利用优化BP 神经网络建立裂缝宽度预测模型
何涛,谢显涛,王君,赵洋,苏俊霖,3
(1.中国石油天然气集团川庆钻探工程有限公司,成都 610000;2.西南石油大学油气藏地质及开发工程国家重点实验室,成都 610000;3.西南石油大学石油与天然气工程学院,成都 610000)
0 引言
在石油钻探过程中,井漏是最常见的井下复杂情况之一[1],它具有发生频率高、诱因复杂、解决困难等特点。裂缝性地层漏失是井漏中最为难缠的问题,据统计,全球石油行业每年裂缝性地层的堵漏花费占到了井漏总花费的90%以上[2]。应对裂缝性漏失主要采用凝胶堵漏、桥塞堵漏、水泥堵漏以及复合堵漏方法[3-4],但是堵漏成功率依然偏低,这很大程度上归因于裂缝宽度难以确定。我国目前判断裂缝宽度还是以经验法为主,即根据以往的堵漏经验来判断裂缝宽度,并根据判断结果选择堵漏方法及堵漏材料,这种常规方法很难保证裂缝堵漏的一次成功率,故而裂缝宽度的预测问题亟待解决。
赵洋等人[5]建立了Griffiths 天然裂缝宽度预测模型,并通过数值解法确定了裂缝宽度的部分影响因素;李黔等人[6]建立了实钻漏失特征曲线的计算模型,通过该模型可以加快图版法的Lietard天然裂缝宽度预测,并提高准确率;陈曾伟等人[7]基于地层裂缝产生的岩石力学机理建立了BP 神经网络模型,并通过现场数据实验初步肯定了BP 神经网络的预测效果。
由文献调研可知,目前裂缝宽度预测方法尚不成熟。因此,提出利用优化神经网络预测裂缝宽度的方法。通过BP 神经网络对井史数据的地质参数、钻井液参数、位置参数等进行了深入的挖掘,利用方差分析(ANOVA)法确定了影响裂缝宽度的相关参数,并将参数输入优化的BP 神经网络模型进行训练,建立了预测裂缝宽度的BP 神经网络优质模型,通过样本数据拟合、模型性能评估及现场工程检验等方法验证了预测精度。
1 研究准备
1.1 数据采集
本次研究数据来自川渝地区C 区块,该区块地形为丘陵山地,以变质碎屑岩为主,海拔大约在300 m~700 m 之间。石油工业与计算机领域的成功融合,使井史资料的数据采集更加的方便,钻井液密度、漏斗黏度等参数可以电脑直接采集,而裂缝宽度则通过排量及漏速等参数进行反推得到(天然裂缝与诱导性裂缝产生原因不同,但漏失机理基本一致,因此不必区分),这些参数为神经网络模型提供了重要的信息来源。
1.2 数据处理
井史数据处理是井史数据挖掘工作必不可少的一环,在一个完整的大数据模型形成过程中,数据处理过程占据了总工作量的70%左右,而杂乱无章的、包含噪点值及缺失值的数据会对产生的模型造成极大的影响。由于国内针对大量、杂乱的井史数据尚无明确的处理办法,因此本研究将数据处理作为一项重点内容进行详细阐述。
1.2.1 数据集成与整理
使用Python 开发环境,开发数据集成模块,分别将其对应的16 张EXCEL 综合数据表迁移到MYSQL 数据库中,形成处理历史数据,一共有64口井、近20 万条井史数据记录,整理结果见表1。

表1 数据集成与整理结果
1.2.2 数据清洗
数据清洗阶段主要包括噪点处理和缺省值处理。该阶段对原始数据仓库中的所有数据表增加ID 索引主键字段,增加使用标志字段,用来记录某条数据是否已被推送到清洗数据中,凡已推送的记录并将值记1,新进入的未被推送的数据记录其值记为0,利用这种方法可以对井史数据进行最简化的处理。
本研究井史数据噪点处理采用数理统计思想,即首先计算每口井各项参数的均值μ 和标准差σ,并判断每口井各项参数的分布情况,将各项数值型参数的分布情况统一划分为正态分布、泊松分布、威布尔分布以及不属于任何分布的无分布情况。
对于正态分布采用Grubbs 检验方法,即先把数据按照从小到大的顺序排列x1,x2,x3…xN,从该参数(通常每个油井各项数据数量在3000~5000个左右)中挑出50 个疑似噪点,再计算其统计量。

式中,xi表示疑似噪点,avg 表示均值(与μ 含义一致),s 表示算术估计量。
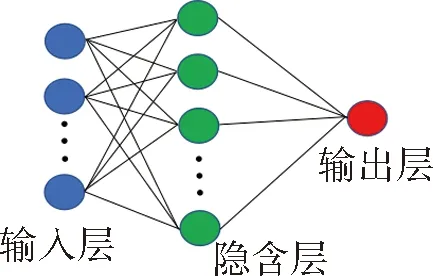
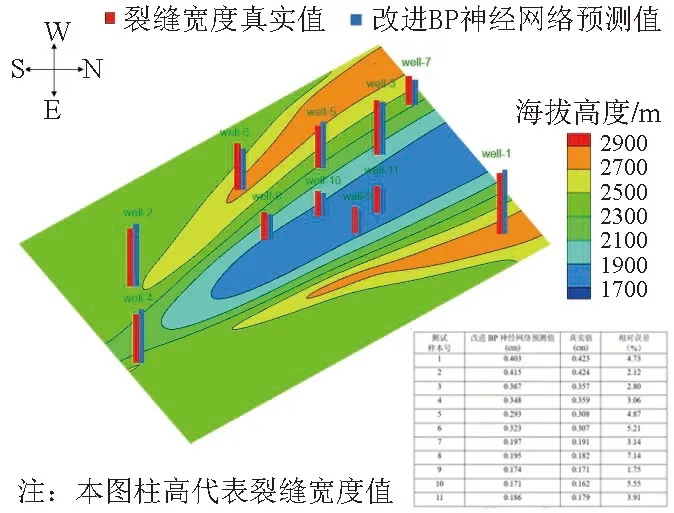
查阅Grubbs 检验法的临界值表可得g(a,n),将其与gi进行比较,如果gi 对于无分布情况则采用箱型图法判断噪点,箱型图识别异常值的标准为:小于QL-1.5IQR 或大于QU+1.5IQR 的值。QL称为下四分位数,表示全部观察值中有四分之一的数据取值比它小;QU称为上四分位数,表示全部观察值中有四分之一的数据取值比它大;IQR 称为四分位数间距,是上四分位数QU与下四分位数QL之差,其间包含了全部观察值的一半。利用该方法判断无分布情况下井史数据噪点的部分参数结果见图1。 图1 部分噪点数据箱型图 本研究数据缺省值处理采用查找法和牛顿插值法两种,分别对应层位、岩性等文字信息缺省值和立压、流量等数值信息缺省值。查找法需要根据钻井液性能数据中某一口取样井深,到岩性记录数据中对应井号、起始井深、终止井深去对应,将对应的层位、岩性、钻头型号、钻井液类型信息补到对应的数据中,经过检测缺失值为0。而在数值型数据中,将缺失率小于5%的信息所对应空值行删除,不会影响后面数据处理。对钻井液密度、立压等重要数据,对于其缺失率在5%~30%之间,采取牛顿插值法补充,补充后全部补齐,缺失率为0。 1.2.3 数据归一化 数据归一化可以消除指标之间的量纲和取值范围差异的影响,需要进行标准化处理,将数据按照比例进行缩放,使之落入一个特定的区域,便于进行综合分析。本研究的井史数据中大钩负荷是除井深外数值最大的参数,其最大数值为2114.2,并且均值为1364.3,六转读数是数值最小的参数,其最小非零数值为0.5,均值为29.4,从数据挖掘的角度可知不同参数之间数值大小、同一参数下数值大小及均值差异都不大,故采用最小-最大规范化方法即可,其公式如下。 其中,max 为样本数据的最大值,min 为样本数据的最小值,max-min 为极差。 该方法可以将井史数据值映射到[0,1]之间,不仅计算量小,而且保留了原来数据中存在的关系,对于不同参数数值之间、同一参数的数值之间均差距不大的井史数据来说不失为一种最佳选择。 将收集到的280 组漏点数据样本进行数据处理后,剔除了16 组不合格的样本,将剩余的264 组数据作为优化BP 神经网络的输入数据。 1.2.4 参数选择 在数据挖掘的准备工作中,参数选择是直接决定模型性能的一项工作,参数选择的参考依据即为相关性分析,目前我国相关性分析最常用到的方法包括图表分析法、相关系数分析法、多元回归分析法、多因素方差分析法。由于井史资料庞大繁杂,且参数之间非线性相关,因此图表、相关系数、多元回归均无法完成,因此本研究采用多因素方差分析来进行参数选择依据。 利用SPSS 软件对清洗后的钻井井史数据进行多因素方差分析,将层位、钻压、钻速等20 个井史数据参数定义为方差分析的自变量,裂缝宽度作为因变量,最终得到参数显著性结果见图2。 图2 裂缝宽度相关参数方差分析显著性(P 值)统计直方图 通常来说多因素分析的P 值中的α 取0.05 或0.1,本文为了尽可能考虑到更多的裂缝宽度预测影响因素,取α 为0.1。因此根据上图结果选定方差分析中对裂缝宽度因素影响较大的16 个参数作为神经网络的输入参数,分别为:层位、岩性、钻头尺寸、钻头型号、扭矩、钻速、钻压、转速、立管压力、漏斗黏度、φ100、φ300、钻井液类型、钻井液密度、钻井液初切。 BP 神经网络结构简单、使用成熟、应用广泛。网络一般包含输入层、隐含层、输出层3 层构成,典型BP 神经网络结构[8]见图3。网络包含了正反2 个方向的数据流向[9]。其一,数据从输入层传递到隐含层再传递到输出层,为其正向传递[10];其二,如果数据训练未能达到预定的误差值,则其反向传播,即从输出层传递到隐含层再传递到输入层,来修正权重和阀值从而修正神经元间的联系,直至误差达到预先设定值,训练结束,建立训练模型。 图3 BP 神经网络结构图 本次裂缝宽度预测模型为了全面考虑主要参数对裂缝宽度预测的影响,将对裂缝宽度因素影响较大的16 个参数作为神经网络的输入参数,以反推出来的裂缝宽度值作为标准训练输出,以裂缝宽度作为BP 神经网络的输出参数。 采用三层神经网络结构模型,根据BP 神经网络预测裂缝宽度特征量的选取可知输入层为16 个神经元,分别用来表示表1 中的16 项参数输出层设置为1 个神经元,即裂缝宽度。 本网络输入层与输出层之间的神经元个数分别为16 和1,采用下式来计算隐含层节点[12-13]个数k。 式(3)中,n 代表输入层神经元个数,m 代表输出层神经元个数,a 是介于1~10 之间的常数,故k 为5~14。选择不同的k 值训练模型[11]。最终通过重复验证发现,k 为11 时模型误差最小,故而令该模型最佳隐含层神经元个数为11。 BP 神经网络权值Wi与阈值bi初值的确定是神经网络中重要的一个环节,虽然在网络计算中Wi和bi都是变化值,但两者初始值的随机性会给BP 神经网络模型带来很大的不确定性,从而影响BP 神经网络预测的准确率。笔者采用文献[12]中提出的第三种权重阈值初始化方法,即使用阮维德罗算法进行第一次初始化,并且令b1、b2为0,在此基础上采用randperm 函数随机产生隐藏层到输出层的权重参数。这种方法可以有效地消除权值和阈值的相关性,避免网络权值和阈值在学习调整过程中互相干扰。 由此,BP 神经网络基本模型构建完成,接下来只需要设置训练参数即可。本次模型训练参数如下:①网络学习速率为:0.05;②目标误差为0.001;③量系数取值为0.9;④最大训练次数为1000 次。 由于BP 神经网络中各节点之间交流的形式为非线性函数,故而计算过程相比于其他方法要复杂很多,尤其在参数众多的情况下,参数的数量在很多情况下可以直接影响到计算精度,若是不经过数值优化,就很容易影响权值的变化情况,最终导致预测结果偏差较大。因此本次研究将扩展拟牛顿法(L-BFGS 法)与BP 神经网络裂缝宽度预测模型结合起来,从而大幅度地提高了模型本身的预测精度。 L-BFGS 方法是由数学家们根据数据快速优化问题提出的一种成功的范例,它是在牛顿法的基础上进行的,其相比于传统BP 神经网络权值、阈值迭代的梯度下降法来说,不仅迭代速度更快、更能通过不断储存海森矩阵的方式来稳定权值及阈值,从而避免BP 神经网络陷入局部最小。依据神经网络参数和结构的设定原理,利用L-BFGS 算法优化BP 神经网络的工作流程如图4 所示。 图4 融合L-BFGS 方法的BP 神经网络工作流程图 本文应用L-BFGS 方法优化BP 神经网络的权值和阈值,步骤如下。 ①定义初始权重、阈值和允许误差,存储最近迭代次数m=6,并令k=0,H0=I,r=▽f(x0),其中初始海森矩阵H0暂定为单位矩阵,f(x0)初始设定为双曲正切函数。 ②开始迭代,判断||▽f(xk+1)||≤θ 成立,则返回最优解xk+1,否则转至下一步; ③确定此次迭代方向pk与步长αk,并利用下式开始计算: ④更新权值x,并在k >m 时保留m 次向量: ⑤计算下列式子并保存: ⑥令rk=Hk▽f(xk),叠加次数后,转步骤(2)。 将收集整理的264 组数据按照3 乐1 的比例分为训练集和测试集,即198 组用于训练BP 神经网络,66 组用于测试其准确性,最终测试得到结果见图5,预测值与实际值之间的趋势线斜率达到0.8772,截距达到0.0206。 图5 裂缝宽度预测结果数据拟合曲线 为了证明所提出的优化BP 神经网络模型裂缝宽度预测结果的可靠性,选择了模型评估中最常用到的3 个指标来计算[12],分别是确定系数R2、皮尔逊相关系数PCC 和均方根误差RMSE。其公式如下。 选择具有最佳模拟结果的BP 神经网络对训练和测试数据集进行模型性能评估,计算结果见表2。 表2 优化BP 神经网络模型性能评估 中国西部某油田C 区块是井漏事故的频发地区,平均每口井都有4 次左右的井漏事件,并且一次堵漏成功率较低,即使是经过了桥塞堵漏、水泥堵漏甚至复合堵漏,仍然可能会出现流体反复漏失的问题。究其原因,除了该地区地层构造复杂,天然裂缝较多之外,漏失裂缝宽度未知也是关键因素之一。 为了更好地了解神经网络缝宽预测模型的可行性,收集整理了11 组现场工程实例,并通过成像测井实测对应的裂缝宽度,将钻井液密度、层位等参数作为模型输入参数,裂缝宽度作为目标参数,进行实例预测,最终结果见图6。 图6 优化BP 神经网络裂缝宽度预测模型现场应用结果 可以看出,除了8 号样本误差较大(接近10%),其余样本的拟合程度都相当高(误差不到5%),大部分样本预测值与实际值之间不超过0.2 mm。由此表明,该方法构建的BP 神经网络预测精度较高,可以用于裂缝宽度预测。在现场堵漏施工过程中可以通过这种方法来预测裂缝宽度,并根据预测缝宽来选择堵漏颗粒粒径大小及材料,从而提高一次堵漏成功率。 1.提出了利用优化BP 神经网络模型进行井漏裂缝宽度预测模型建立的方法。该方法在权重推导方面不同于传统神经网络的梯度迭代法和拟牛顿法,极大的提高了裂缝宽度预测模型的精度,为石油勘探开发中很多问题的解决提供了新的思路。 2.针对本次建立的BP 神经网络模型分析可知,在各个裂缝参数中,钻井液密度、层位、岩性、钻井液初切这4 项参数对裂缝宽度预测结果影响极大,其次是钻压、钻头型号、扭矩、φ100、钻井液类型、转速等参数。


2 BP 神经网络
2.1 BP神经网络原理
2.2 BP神经网络裂缝宽度预测模型

2.3 BP神经网络的优化

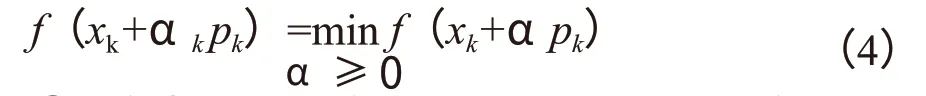


3 BP 神经网络预测结果



4 裂缝宽度预测模型的应用
5 结论

