球形粒子与手征平面的耦合散射

方玉龙，孙玉发，张华永

1.黄山职业技术学院医学系，安徽黄山,245000;2.安徽大学电子信息工程学院，安徽合肥,230039

手征媒质具有新奇的电磁特性，例如：旋光性、 圆二色性和负折射现象等，正是这些特性使其在化学、生物学、光学和微波技术等领域得到广泛应用。从电磁本质上来说，手征媒质可以引起电场和磁场之间的耦合，体现在其本构关系与电场和磁场均有关。电磁波经过手征媒质时的散射特性是手征媒质电磁特性研究的重要内容，为此很多学者已经提出了多种理论和方法。其中，既有矩量法[1]和时域有限差分法[2]等数值方法,还有广义Mie理论[3]和T矩阵法[4]等解析或半解析方法,它们成功解决了电磁波经过手征球、圆柱以及任意形状物体的散射问题。然而，这些研究还仅限于单个的散射体，对于存在手征结构的多个散射体之间的耦合散射仍然是一个重要的课题。例如，手征平面与其上方球形粒子之间的耦合散射既具有重要的理论意义，同时在激光缺陷检测、粒度分析、粒子操控以及近场超分辨成像等领域展现出了广阔的应用前景[5-7]。本文基于一种精确的解析方法，对上述耦合散射问题进行详细研究。

1 理论公式

在自由空间传播的平面波入射到半无限大手征媒质上，即在手征媒质的上方有一介质球形粒子，其在直角坐标系Oxyz中来描述，而z=d为自由空间和手征媒质的分界面，如图1所示。入射波在分界面上会发生反射和折射，其中入射波和反射波照射到球粒子上将被散射。球粒子向下的散射场入射到分界面上，又会引起反射和折射，进一步引起球粒子的散射。这样在分界面上的反射和球粒子的散射就会无限次的进行下去，此现象称为球粒子和手征平面之间的耦合散射。显然，耦合散射是一个复杂的过程，但是作为整体来说可以采取如下两个步骤进行研究。

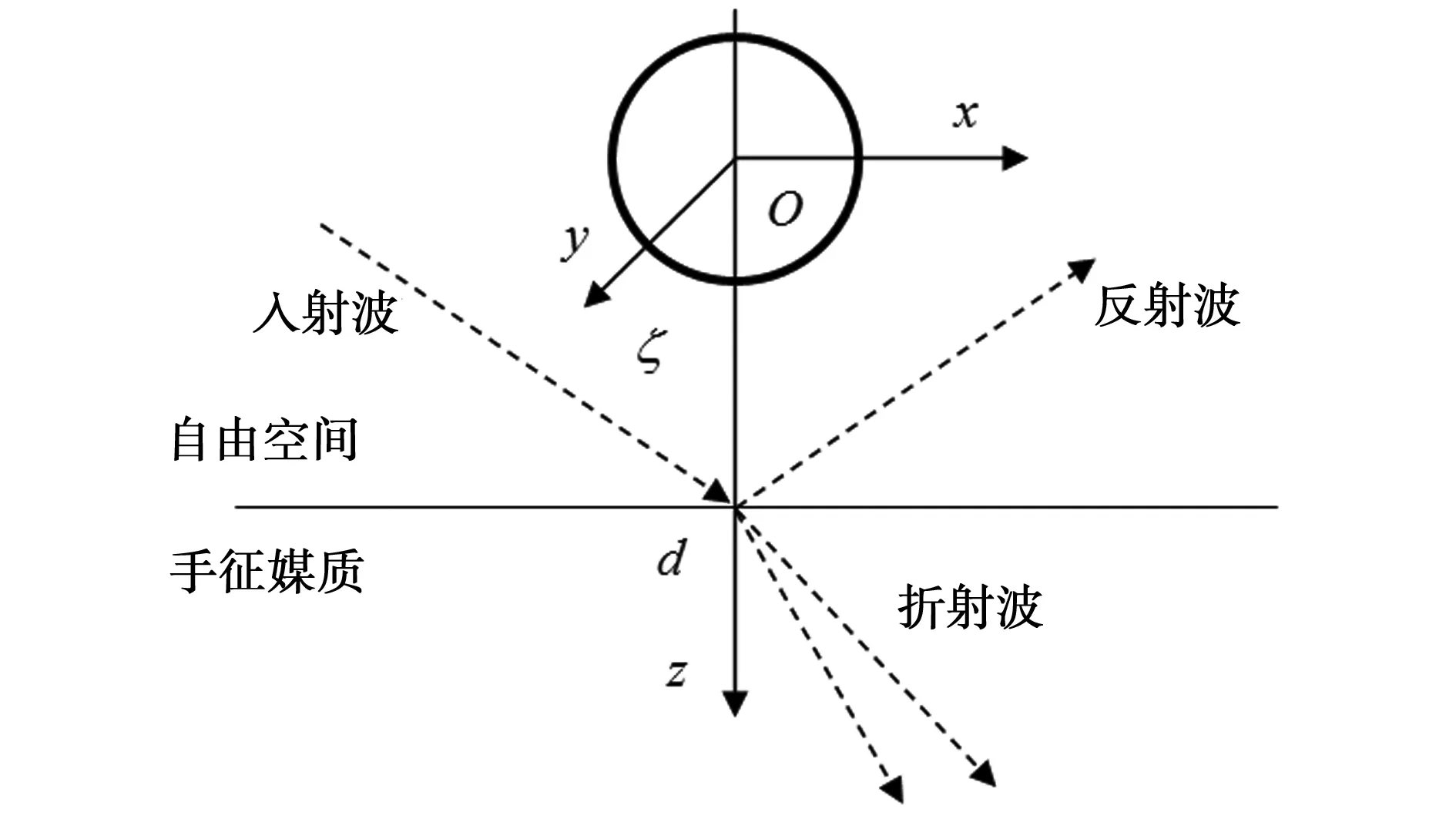
图1 平面波入射下球粒子和手征平面耦合散射图

1.1 球粒子不存在时平面波的反射和折射

入射平面波的电场和磁场可以用圆柱矢量波函数展开如下：

(1)

(2)

反射平面波的电场和磁场也可用圆柱矢量波函数相应的展开为：

(3)

(4)

(5)

(6)

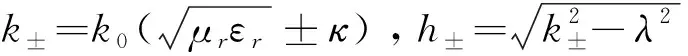
方程(1)—(6)中的展开系数可由如下的电磁场边界条件确定：

(7)

其中下标r和φ分别表示相应电磁场的r和φ分量。

把方程(1)—(6)代入方程(7)中可得如下关系式：

Im,TEeihd+ame-ihd=cmeih+d+dmeih-d

(8)

Im,TMcosαeihd-bmcosαe-ihd

(9)

Im,TEcosαeihd-amcosαe-ihd

(10)

(11)

从方程(8)—(11)组成的方程组即可求出反射场和折射场的展开系数，由于下面只用到反射场，仅给出反射场的展开系数am和bm如下：

(12)

(13)

(14)

(15)

(16)

(17)

把方程(12)和(13)代入方程(3)和(4)，可得反射电磁场用反射系数表示的关系式，在后面研究球粒子和手征平面耦合散射时将用到。

1.2 球粒子与手征平面的耦合散射

虽然耦合散射是一个复杂的过程，但作为整体球粒子的散射场和内部场可分别用第三和第一类球矢量波函数展开如下[8]：

(18)

(19)

为了下面在分界面z=d上应用边界条件，需要把散射场用球矢量波函数展开的表达式，即方程(18)转化为圆柱矢量波函数的形式，为此需要用到如下的转换关系式[10]：

(20)

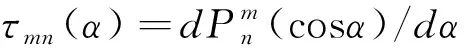
把方程(20)代入(18)，可得散射场用圆柱矢量波函数展开的关系式为：

(21)

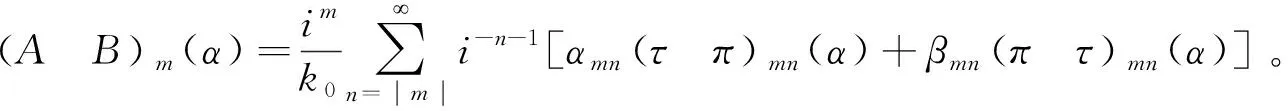
同理，虽然球粒子和手征平面之间存在耦合散射，但作为整体散射场的反射场仍可用圆柱矢量波函数展开，其中的反射系数与方程(14)—(17)一致，具体可表示为：

(22)

把参数(AB)m(α)代入方程(22)，可得：

(23)

(24)

为了求解方程(18)和(23)中的展开系数αmn和βmn，还需用到球粒子表面的边界条件：

(25)

(26)

(27)

(28)

(29)

其中Umn′n,Vmn′n,Kmn′n和Lmn′n的表达式分别为：

(30)

(31)

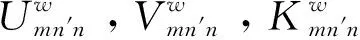
2 数值结果和讨论

通常实际应用中只关心上半平面，即π/2<θ≤π区域内的散射场。取散射场Es及其反射场Ers在k0r→∞的渐近表达式，可定义如下的微分散射截面(DSCS):

(32)

其中λ0为入射波长，其他参数为：

(33)

(34)

为了验证本文的理论方法，图2给出了与文献[11]的比较。文献[11]采用T矩阵法研究了球形粒子与介质平面的耦合散射。当手征媒质的手征参数κ=0时，则手征媒质就成为通常的介质。在图2中，给出了TM极化平面波照射下球形粒子与介质平面耦合散射的归一化微分散射截面，其中球形粒子在介质平面上或在其上方一定位置处，结果与文献[11]中图4吻合的很好。

图2 TM极化平面波照射下的归一化微分散射截面

图3给出了TE和TM极化平面波照射下归一化微分散射截面的比较，其中球形粒子在手征平面上。从图3中可以看出由于手征平面的反射以及与球粒子的耦合散射，使θ=135°和θ=225°处出现耦合散射强度的极大值。与 TE极化相比，TM极化平面波照射下归一化微分散射截面的曲线振荡较少，这可解释为由于TM极化平面波反射的布儒斯特角现象[9]，导致耦合散射较弱。

图3 TE和TM极化平面波照射下归一化微分散射截面

图4(a)和(b)分别展示了不同的手征参数对TE和TM极化平面波照射下归一化微分散射截面的影响。可以看出手征参数对TM极化平面波照射下散射强度的影响较大，这与手征参数对TM极化平面波的反射系数影响较大的结论一致。

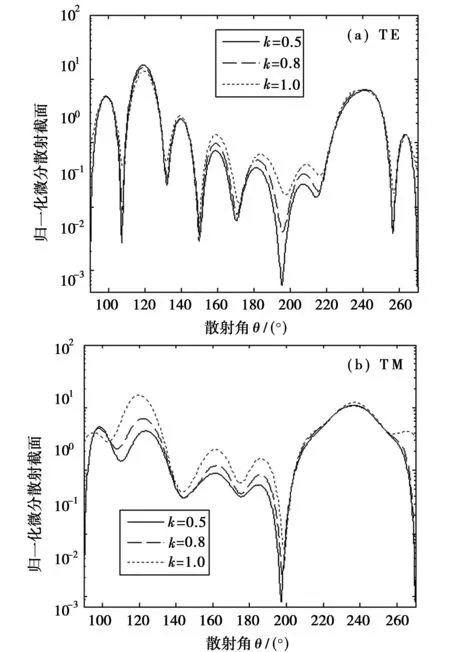
图4 极化平面波照射下的归一化微分散射截面

本文的数值结果由Matlab程序计算，其中用到的球贝塞尔函数和连带勒让德函数这两个特殊函数调用自Matlab函数库。由于采用了精确的解析方法，很多结果已推导出解析表达式，所编的程序占用内存很小，约40 KB。程序在用高斯积分法数值求积分和用高斯消去法求解由方程(26)—(29)组成的方程组时运行较慢，但整体运行时间在一分钟以内，效率较高。

3 结 语

本文通过把相应的场用适当的球或圆柱矢量波函数展开，并应用球矢量波函数与圆柱矢量波函数的转换关系，以及电磁场边界条件，给出了一种研究手征平面与其上方的介质球耦合散射的解析方法。针对不同情况，给出了归一化微分散射截面的数值结果。其中当κ=0时，本文所研究的内容就成了球形粒子与介质平面的耦合散射，结果与有关文献进行了比较，吻合的很好，在很大程度上验证了本文的理论方法。另外结果还表明在θ=π-ζ处出现耦合散射强度的极大值，与TE极化相比，TM极化平面波照射下耦合散射较弱，而手征参数对耦合散射的影响较大。本文的耦合散射理论为进一步研究和应用手征媒质提供了一个新的途径，而耦合散射也在诸多理论和应用问题的研究中体现出了重要的价值。