面向精准农业中的高维复杂数据的降维方法

许新华 吴海燕

(郑州西亚斯学院,河南 新郑 451150)

引言

当今社会，在传统农业的生产过程中，因为市场的不稳定、天气的变换、病虫害的破坏、水肥的不合理施用等因素对其产生了较大的影响[1-3]。因此，要根据现代农业的要求实现精准生产，就要做到对天气条件精准管理，对病虫害的破坏程度实现精准喷药。在现阶段精准农业发展过程中，各种现代化信息技术的应用需求越来越大，衍生出来的复杂数据(规模大、流转快、类型多样、价值密度低)也越来越多[4-6]。目前，我国在对农业生产过程中各种信息数据的提取和处理上，针对一些高维、异构、非线性、不完全、不精确等复杂数据，还在沿用相对陈旧的处理方法，在精准农业中，对搜集到的数据结果分析往往效果不理想，隐藏在这些数据中的信息或潜在的特点无法被探知或者有效利用，导致“数据资源”变成“数据灾难”，精准农业的产生及发展就是要主动去挖掘和利用这些潜在数据中的特点或规律。因此，如何有效地从高维复杂数据中获取信息或规律已成为当今中国精准农业发展的瓶颈，必须寻求高效、优质的处理方法，才能让精准农业快速发展。其中，主分量分析(PCA)[7]、独立分量分析(ICA)[8]、多维尺度变换(MDST)、线性判别分析(LDA)、基于核的主分量分析(KPCA)、遗传算法(GA)、小波变换(WT)、自组织特征映射(SOM)等技术[9-14]是常见的数据提取方法。其中既包括线性特征提取方法，也包括非线性特征提取方法。线性方法虽然计算简单，但对数据出现非线性分布规律时，特别是流行分布数据时，并不能很好的发现。出现的一些非线性方法虽然可以解决这些问题，但在迭代优化过程中，计算量加大，且会陷入局部最优。虽然现在标准不统一，面对不同问题有针对性的选择合适的方法，但主要还是集中在对数据要求高，当数据存在噪声或者分布不均、数量减少时，降维效果往往不够理想。本文为了克服数据非线性分布带来的困扰，在原来已有算法的基础上，提出了一种局部非线性嵌入(LNE)算法，将其用在高维复杂数据的降维上，效果明显。

1 局部线性嵌入(LLE)

1.1 数据降维经典算法介绍

数据降维包括线性算法和非线性算法,线性降维方法思想简单，复杂度低,在实际问题中得到了广泛地应用,且在数据降维算法中具有重要地位,处理复杂数据的优势更明显于线性算法。PCA和MDS是现有的经典的数据降维算法，而Isomap、LLE和LE是具有代表性的流形学习方法。该方法认为数据在高维空间中分布复杂，局部却存在欧氏空间，这一发现可以实现先局部后全局，即先在局部建立降维，然后再延伸到全局。这种方法对处理具有非线性结构分布特点的复杂数据效果较好。先列出一些记号，以方便后面的描述。D维空间样本矩阵用X=(x1,x2,…,xn)∈RD×n表示，降维后的d维空间点矩阵用Y=(y1,y2,…yn)∈Rd×n表示，其中xi与xj之间的距离用d(xi,xj)表示，W∈RD×d是转换矩阵，I是单位矩阵。

主成分分析(Principal Component Analysis，PCA)，以线性约束为条件，尽可能使降维后的数据点分散，分散程度用方差大小表示。经典的数据降维算法还有多维尺度分析(Multidimensional Scaling,MDS)，该算法的思想是使降维前后任意两点之间的距离近似相等，采用的是欧氏距离计算。等度量映射(Isomap)是一种改进算法，是MDS算法的补充，一直被认为是流形学习方法的一种代表性算法。Isomap认为若要准确反映数据的内在结构，MDS采用的欧氏距计算结果则不能充分说明问题，应当使用测地距离来计算。而拉普拉斯特征映射(LE)体现了局部的距离关系，更好地说明了问题所在。LE最大的特点是能够降低计算复杂度，提高稳定性。

1.2 局部线性嵌入

局部线性嵌入(locally linear embedding,LLE)，主要体现在数据的局部线性关系得到保持，该算法的思想是先计算每个点的重构系数，然后计算低维嵌入坐标，在这里需要注意的是计算加入重构系数后[15]。于是有如下步骤。

为空间样本矩阵中的点xi寻找k个相邻点，此时用Qi表示相邻点集合，然后计算xi的线性重构系数wi：

(1)

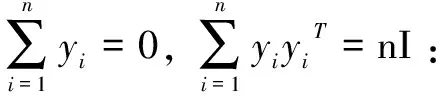
(2)

LLE算法中的核心就是重构系数的建立，如何对重构系数进行计算。由公式(1)可知，wi，i=1,2,…,n之间是相互独立的。计算方法：xi的k个近邻点组成的矩阵用Γ=[xQi(1),xQi(2),…,xQi(k)]∈RD×k表示，k个xi组成的矩阵用X=(x1,x2,…,xn)∈RD×n表示，则：

=‖Xwi-Γwi‖2

=(Xwi-Γwi)T(Xwi-Γwi)

=((X-Γ)wi)T((X-Γ)wi)

=wiT(X-Γ)T(X-Γ)wi

=wiTGwi

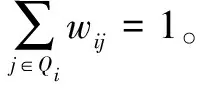
因此，wi由下式计算：

式中，e=(1,1,…,1)T。构造拉格朗日函数：

L(wi,γ)=wiGwi-γ(wiTe-1)

(3)

式中，γ是拉格朗日乘子。对公式(3)分别关于wi和γ求导，可得：

(4)

由公式(4)可得：

(5)

据公式(2)中低维坐标的计算可以由公式(5)重构系数嵌入，李杨[5]给出了计算方法。

由以上可以看出每个xi的重构系数wi中均包含高维数据中的局部信息，并且可以很好地将此类数据的特征保持到低维数据中，wi的优劣关系降维能否完成。图1b是用LLE对图1a中3000个点的s形曲面的降维结果。

从图中采用LLE降维的效果可以看出，结果的鲁棒性较好，但图1a中存在有噪声点的数据，没有得到令人满意的降维。

2 局部非线性嵌入(LNE)

2.1 局部非线性嵌入算法介绍

由以上结论可知，若数据中存在噪声，采用局部线性嵌入算法得到的降维效果不尽理想，前文所提到的降维算法对上节中的问题也不能很好的克服。基于此，本文提出局部非线性嵌入(locally nonlinear embedding，LNE)算法，从降维效果以及应用范围来看，LNE这一改进算法均有显而易见的效果。

若数据中存在噪声点，则点之间局部的线性关系不能保持，此时LLE在噪声数据的降维中效果失效，那么就要找出数据间的某种非线性关系。从线性关系到非线性关系，需要思考2个问题：非线性关系怎样表示，合适的非线性关系如何找到。为解决第1个问题，在每个近邻点上施加一个RD→RD上的映射，据此LNE的计算权值公式:

(6)

由公式(6)可知，LNE的思想是用映射φi作用在xi的每个近邻点xj上，然后再计算权值，点不同映射也不同。针对低维坐标的计算上，LNE与LLE一致，当φj取单位映射时，LNE和LLE算法一样。需要明确的是，LNE和KLLE[16]是不同的，KLLE是高维空间的降维，LNE是在同一维度中进行降维。

2.2 实验结果

对LNE算法在结果部分的展示，仍旧采用3000个点的S型曲面为例,图2是用该算法对图1a进行降维的结果。

从LNE降维的效果可以看出，与LLE相比，对于图1a中有噪声点的数据降维得到了满意的效果。

3 总结

LLE作为流形学习中的代表算法，有较高的知名度，主要表现在该方法可以很好揭示高维非线性数据隐藏在低维空间中的内在结构。然而，LLE也有其无法解决的问题，其降维思想是要使数据局部线性关系很好地维持，若此种关系被破坏，那么结果也有缺陷。实际上，在农作物生长过程中采集的数据大多含有噪声，而噪声的存在往往会破坏数据局部的线性关系。在当前精准农业的背景下，本文提出了LNE算法，主要解决当局部的线性关系得不到满足的情况下，挖掘数据间的某种非线性关系，本文算法可以看作LLE的扩展和完善，或者说当满足某种映射关系时，LLE就退化为LNE。

在精准农业的要求下，研究高维复杂数据处理算法，优化复杂数据，提炼出数据精准信息，从而方便精准地获取农作物的生长情况，指导工作人员对农作物生长环境进行监控，实现所提出的精准农业的要求。