随机时延下非线性多智能体系统的一致性控制研究

罗俊芝，张雪飞，詹环

（陆军装甲兵学院基础部，北京 100072）

多智能体系统是由多个智能体组成的集合，智能体之间以及智能体与环境之间通过通信、协商与协作来共同完成单个智能体所不能解决的问题。多智能体系统有着广泛的应用背景,比如航天器的编队控制问题，水下多机器人系统的勘探任务分配问题等，都可以转化为多智能体系统的控制问题。随着科技的发展，一项复杂的任务可以通过多个结构、功能都相对简单的智能体来完成。因此，多智能体系统的控制研究已经成为了一个热门的研究方向。如文献[1]对多智能体系统的队形控制方法及应用进行了综述，给出队形控制的研究概况；文献[2]通过引入虚拟领导者产生期望轨迹的方法，研究了离散时变多智能体系统有限时间一致性控制；文献[3]则基于脉冲控制，针对时延异构多智能体编队控制进行研究；文献[4]则对无人机编队形成与防碰撞进行研究，提出了基于信息一致性的无人机编队形成时避免碰撞的控制策略；文献[5]在研究了时变拓扑结构下，系统有Leader 领导下多智能体系统的跟踪控制问题。文献[6]研究了时变拓扑网络结构下的多无人机系统的一致性控制问题；文献[7]研究了时变拓扑结构下的多无人机领航跟随一致性和轨迹跟踪问题；文献[8]研究了具有时滞和时变系数的离散多智能体系统的一致性。尽管目前关于多智能体系统的研究成果颇多，但是大部分研究是在系统线性模型的基础上展开的。由于多智能体系统的实际背景比较复杂，线性模型不能够精确描述多智能体系统的模型，因此基于非线性模型的多智能体系统研究更有意义。目前已有一些研究成果对此进行了关注[9-16]，如文献[9]利用滑模控制研究非线性多智能体系统一致性控制问题；文献[10]则针对非线性传输的多智能体系统的自适应一致性控制问题进行了研究；文献[11]关注了脉冲控制下的非线性多智能体系统部分分量一致性问题。文献[12]针对一类非线性多智能体系统，研究了满足预定性能的协同控制问题；文献[13]研究了非线性多智能体系统的输出调节问题，等等。该文基于多智能体系统的非线性模型，研究系统的一致性控制问题，考虑到智能体之间信息传输通过网络进行，传输效果与网络环境有很大关系，如果网络环境不好，可能造成信息传输时滞存在较大差异，考虑到智能体之间信息传输的实际情况，该文引入网络时滞延迟值的概率分布模型，对非线性多智能体系统的一致性控制进行研究。

该文从系统的非线性模型入手，假设系统的各节点之间信息传输时存在时滞，并且假定已知网络传输延迟值的随机分布，也就是网络传输时滞取定某些数值的概率分布已知，把多智能体系统进一步建模成非线性时滞系统，给出一致性协议的设计方法，给出系统的一致性控制策略。最后通过数值仿真事例，验证所提方法的可行性和有效性。

1 模型描述

在给出系统模型之前，先给出文中用到的假设和引理。

假设假定非线性函数f(x)满足下面的Lipschitz条件，也就是∀x,y∈Rn，有：

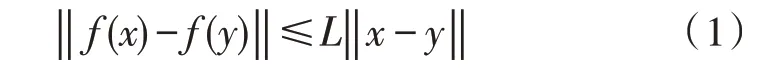
其中，L为一正常数。

引 理若x∈Rn，P=PT∈Rn×n，H∈Rm×n，Rank(H)=l＜n，则下面的条件是等价的：

1）xTPx<0,∀x∈{x∶Hx=0,x≠0}。

2）存在σ∈R，使得P-σHTH<0。

3）∃X∈Rn×n,使得P+XH+HTXT<0。

4）H⊥TPH⊥<0，其中，H⊥是H的核，也就是HH⊥=0。

假设多智能体系统有N个节点Agent 组成,借助复杂网络的思想，用G=(V,E,A)表示这N个智能体构成的拓扑结构，其中V={v1,v2,…,vN} 表示顶点的集合，vi表示第i个Agent；E⊆V×V表示边组成的集合；eij=(vi,vj) 表示从vi到vj的边，权值定义为aij，A=[aij]表示邻接矩阵，其中，aij≥0；L=[cij]表示邻接矩阵对应的Laplace 矩阵。

假设多智能体系统的第i个节点的内部动力学模型表示为：

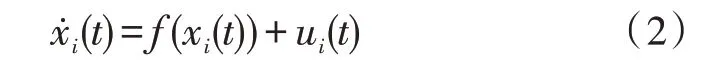
其中，xi(t)∈R2为系统状态变量；f(xi(t))是非线性向量函数，且满足假设1；ui(t)为一致性控制策略，具体设计控制协议时可以根据给出的一致性充分条件得到。

一致性控制协议采用如下形式：

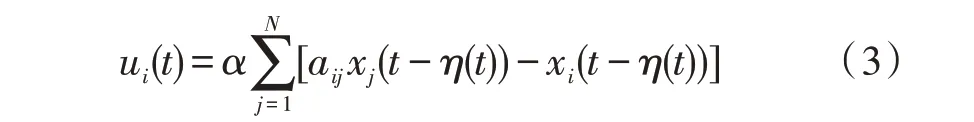
其中，i=1,2,…,N，α是智能体之间的耦合常数，aij是邻接矩阵A=[aij]n×n的元素，η(t)代表信息传递出现的时延函数。

把式（3）代入式（2），得：

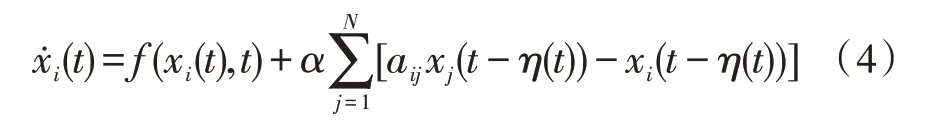
对于给定的两个常数η0和ηm（不妨假设η0≥ηm），定义：

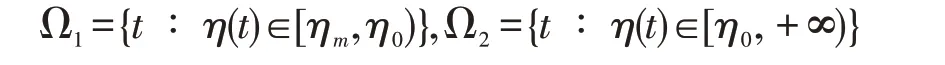
考虑到特别大的网络时延发生的概率非常小，所以总存在常 数ηM≥η0，使得Probη{η(t)∈(ηM,+∞)}=0，也就是时延大于ηM的概率为零，设，并 令，从而存在 0 ≤β0≤1，满足Prob{β(t)=1}=β0,Prob{β(t)=0}=1-β0。

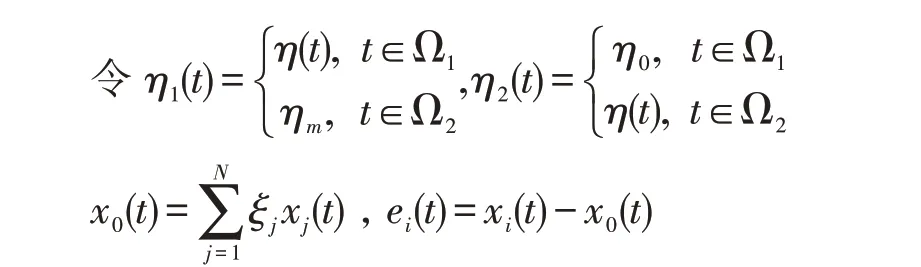
其中，ξ=(ξ1,ξ2,…,ξN)T是A对应Laplace 矩阵的特征向量，且ξT1N=1,ξTL=0。

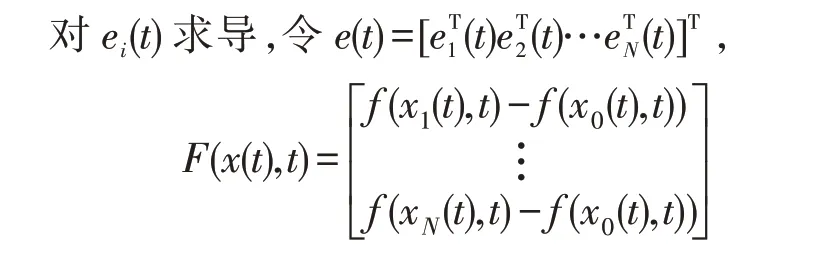
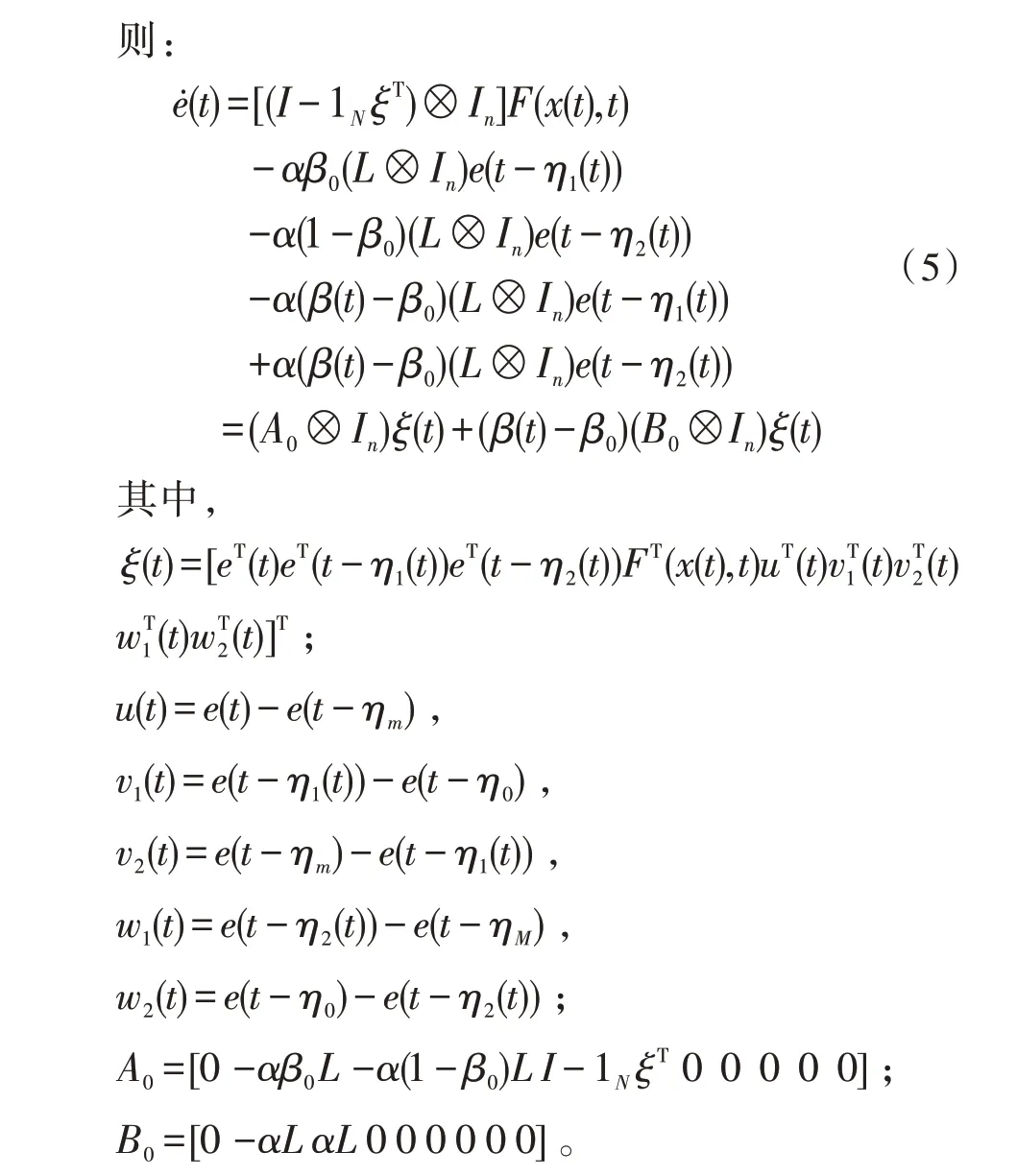
在上述式（5）的模型基础上，根据随机控制和多智能体控制理论，研究系统的一致性控制策略，并给出其存在的充分条件。

2 系统的一致性控制策略

定理对于给定的正常数η0>0、ηm>0、ηM>0 和β0>0，如果存在正定矩阵P>0和Qi≥0，使得下式成立：

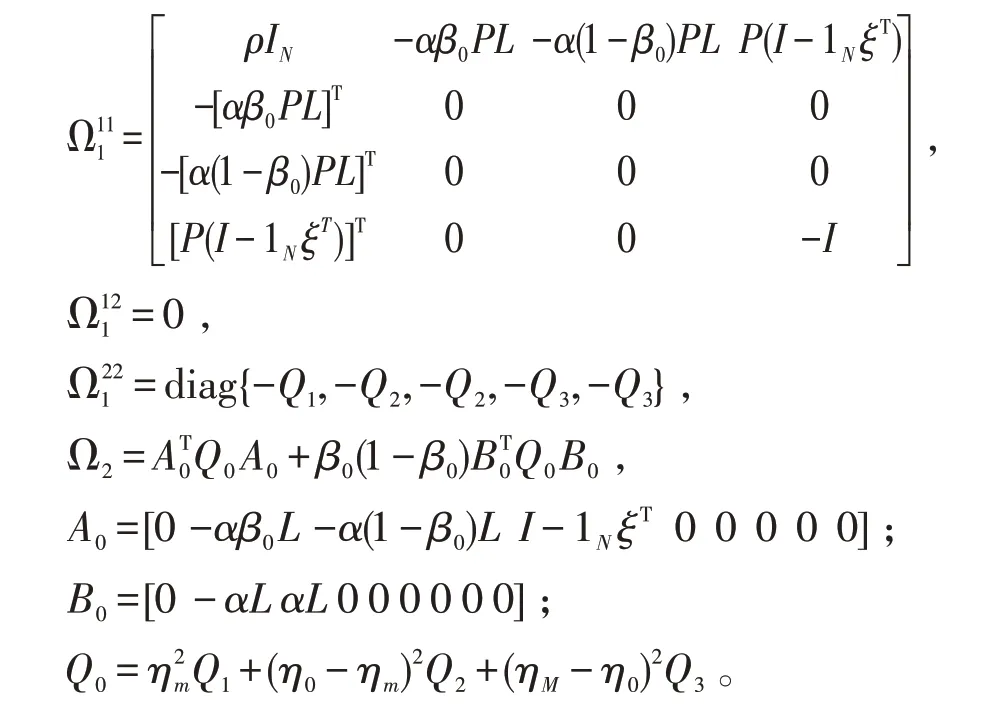
则式（2）的系统在式（3）的控制协议下是渐近稳定的。

证明：考虑式（5）误差系统

若Mξ(t)=0，则：

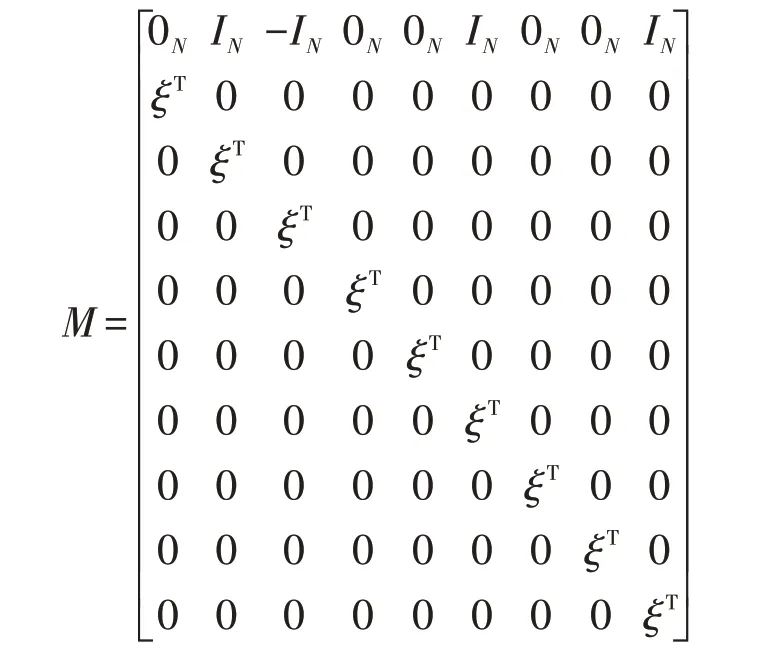
如果(M⊥)TΩM⊥<0，由引理可以得到从而式（5）的误差系统渐近稳定。

3 仿真分析

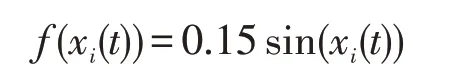
为了讨论方便，假设存在4 个Agent 节点，并且4 个节点之间的关系拓扑为对称拓扑，4 个Agent 之间的彼此信息交互程度相同。取拓扑结构邻接矩阵对应的Laplace 矩阵为如下形式：

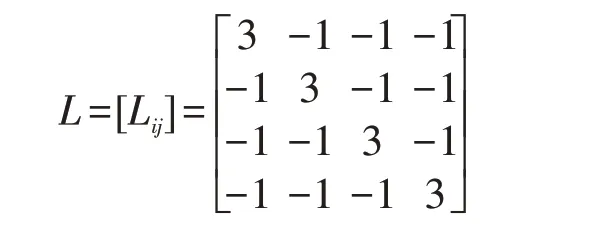
取α=0.5，β0=0.3，η0=0.2，ηm=0，ηM=0.8。

通过求解定理中的条件,可以得到：

取初始状态量x0=(10,5,7,4)，仿真曲线如图1。

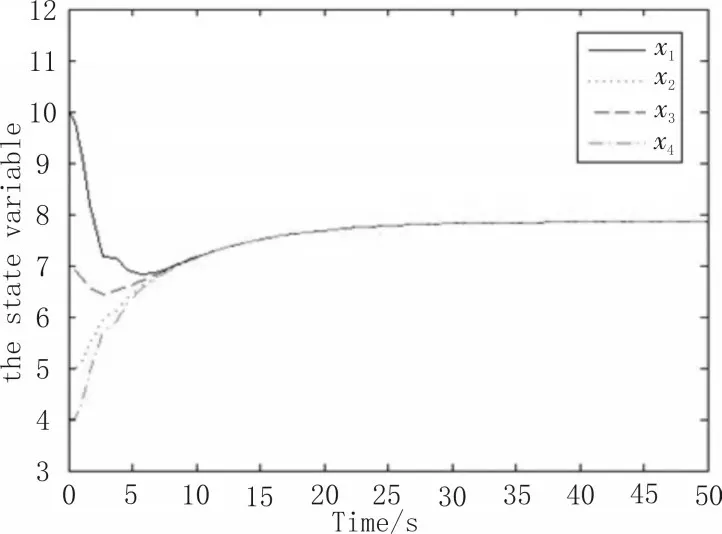
图1 初始状态为x0=(10,5,7,4)下系统的状态变量

图2 初始状态为x0=(10,5,7,4)下系统的控制变量

通过仿真曲线可以看出，系统的4 个Agent 的状态变量能趋于一致，这说明了文中所设计的一致性协议是有效的。验证通过设计与状态时延有关的控制协议，系统中同级Agent 的状态最终能够实现一致性。

4 结论

针对一类非线性系统，首先在假定系统非线性模型满足匹配条件的前提下，研究非智能体系统的一致性条件；其次，针对系统诸节点信息传递的随机时滞的概率分布，把时滞落在某个区间的概率引入系统的模型中，进而借助复杂网络和系统稳定性理论，给出系统达到一致性的充分条件，其与此随机时滞的概率相关，考虑了时滞出现的概率对系统一致性的影响。通过仿真模拟，验证所提控制协议的可行性和有效性。传输时滞的上下界的大小以及出现概率值的大小对于系统的一致性的影响，是下一步要开展的工作研究的重点，也更具挑战性和实际意义。