结合张量与互信息的混合模型多模态图像配准方法

李 培，姜 刚,2,，马千里，薛万峰，杨伟华

1.长安大学地质与测绘工程学院，陕西 西安 710054；2.西部矿产资源与地质工程教育部重点实验室，陕西 西安 710054

随着遥感技术的发展，多模态图像的数量显著增加。不同模态数据之间具有互补性，充分利用这些数据十分必要[1-2]。整合这些多模态数据的关键步骤是图像配准，即将不同时间、从不同角度或由不同传感器拍摄的具有重叠场景的两幅或多幅图像进行配准，是图像处理(如图像拼接[3-4]、目标识别[5]和变化检测[6])的一项基本任务[7-8]。由于不同模态图像的成像机制不同，多模态图像间存在显著的辐射量变化，导致同一地物在不用模态图像中的强度呈现出非线性畸变，这使得控制点的检测变得困难许多。

总的来说，多模态图像配准可以分为基于特征的和基于区域的[9]。基于特征的方法对图像几何畸变的稳健性更强，而基于区域的方法对图像之间的非线性强度差异有更好的抵抗力[10]。基于特征的方法提取稳定、可重复、显著的特征，利用特征之间的相关性来确定最优对齐，它们在多模态图像配准上的主要问题是依赖于图像之间提取重复率高的特征[11]。为了克服这个问题，文献[12]针对光学和SAR图像的固有特点，将光学和SAR图像放在两个Harris尺度空间中检测特征点，提出了OS-SIFT算法。文献[8]提出了PSO-SIFT算法，引入了一种梯度定义，并结合特征点的位置、尺度、方向信息来增强对应点的数量。文献[13]提出了RIFT (radiation invariant feature transform)算法，利用相位一致性 (phase congruency,PC)[14]进行特征点检测，并提出了最大索引图 (maximum index map,MIM)用于特征描述。不过，这些基于特征的方法对非线性强度差异并不具有较好的稳健性，配准精度较低。

基于区域的配准方法是在遥感图像中定义一个模板，然后利用不同的相似度准则搜索最优对应。常用的相似度准则包括误差平方和 (sum of squared differences,SSD)、归一化互相关 (normalized correlation coefficient,NCC)和互信息 (mutual information,MI)[15]。文献[16]提出将互信息与局部梯度信息合成项相乘获得新的相似度准则，提高了配准的稳健性。文献[17]用MI来解决复杂的SAR和光学配准问题。文献[1，18]利用图像的几何结构，构建对非线性强度差异有稳健性的密集描述符，在多模态图像配准中取得了较好的效果。然而，尽管这些方法已经在多模态图像上实现了自动配准，具有高精度配准效果，但仍存在不可忽视的局限性。首先，这些基于区域的方法都需要地理坐标进行正射校正。而且，这些局部描述符或相似度准则的稳健性不强，容易受到噪声影响。

综上所述，多模态图像间存在非线性强度差异与噪声影响，导致多模态图像配准中存在配准精度低、描述符和相似度准则稳健性较差等问题。针对这些问题，本文提出了一种基于混合模型的多模态图像自动配准方案。该方法利用基于特征的方法对齐图像，采用基于区域方法进行高精度配准。在基于区域的方法中，本文采用张量捕捉细微的结构变化，构建密集描述符。但是张量对噪声比较敏感，对它采用各向异性滤波器进行处理，可以降低噪声影响，避免不必要的模糊。在相似度准则方面，张量方向平行度可以很好地解决图像间强度反转的问题。为进一步提升相似度准则的稳健性，本文将张量方向平行度与梯度互信息相结合，充分利用图像结构信息与统计信息。

1 本文方法

本文算法包括预配准与精配准两方面，流程如图1所示。

1.1 预配准

为了使SIFT算法[19]适用于多模态图像配准，可以大致对齐多模态图像对[20]，本文对SIFT算法作出以下3点改进。

(1)多尺度Harris角点代替DoG尺度空间局部极值点：SIFT算法在DoG尺度空间中检测局部极值点作为特征点，而DoG和Hessian矩阵都依赖于二阶导数，会被SAR影像中的散斑噪声严重破坏，不能检测出SAR图像中可靠的特征点[21]。相比之下，多尺度Harris函数[22]是基于一阶导数计算的，Harris角点具有更好的稳定性和重复性。

垂直方向多尺度Sobel算子公式如下

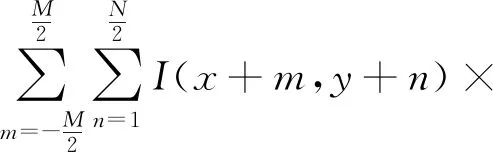
(1)

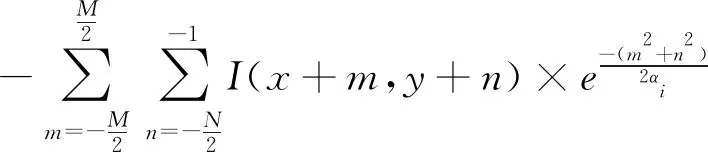
(2)

Gv,αi=Sv1,αi+Sv2,αi

(3)

式中，M和N表示尺度αi下处理窗口的大小；(x,y)表示中心点的位置；I代表原图像素强度；Gv,αi代表αi尺度下的垂直梯度。图2(a)展示了垂直处理窗口，图2(b)展示了垂直多尺度Sobel算子。

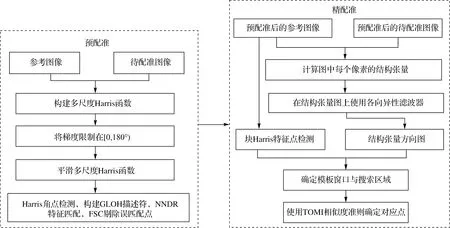
图1 本文方法流程Fig.1 Flow chart of the proposed method

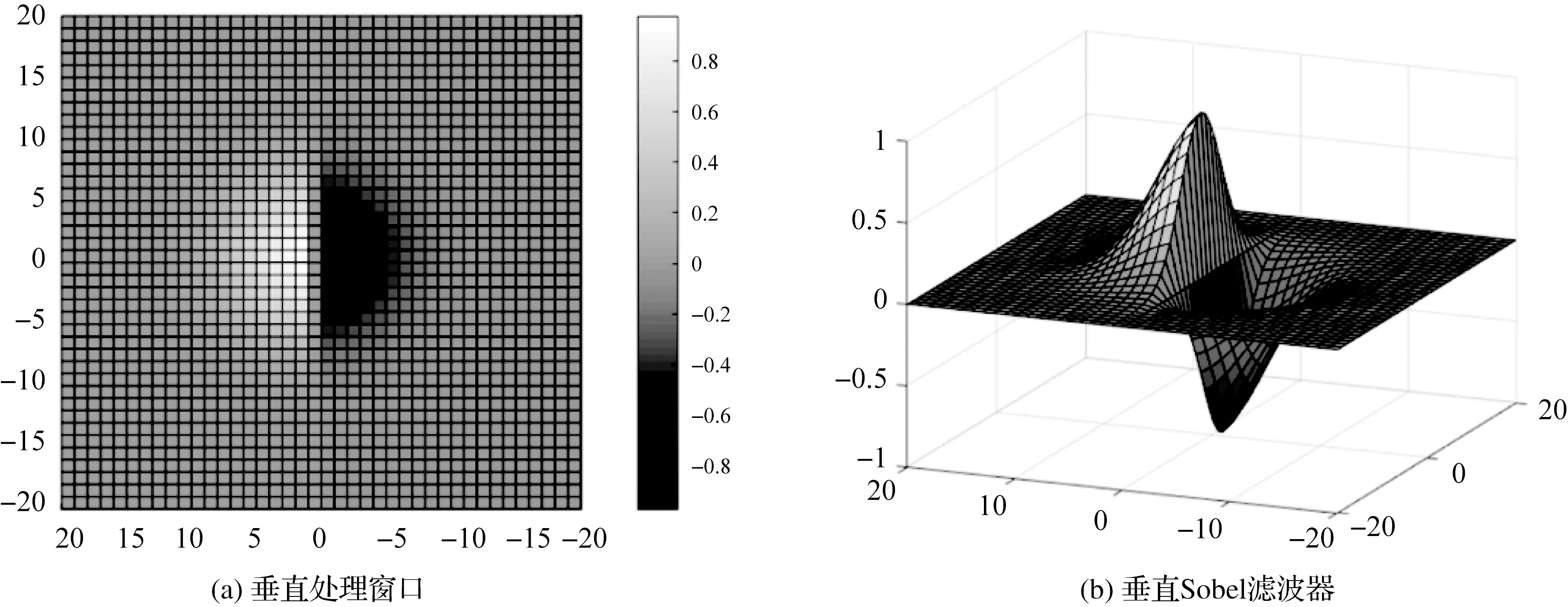
图2 Sobel滤波器Fig.2 Sobel filter

梯度幅值和梯度方向计算如下

(4)

(5)

多尺度Harris矩阵和函数定义如下

(6)

R(x,y,αi)=det(C(x,y,αi))-

d·tr(C(x,y,αi))2

(7)

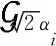
本文计算多尺度Harris函数得到原图的多尺度表示，尺度层数M=5，尺度αi=α1·ci-1i∈[1,2,…,M]。图3展示了两种方法的特征点检测示例，可以看出，Harris检测出来的特征点都落在角点或高亮点上，而DoG方法检测出来的特征点大多落在同质区域。

图3 LiDAR-Optical图像上的特征点点检测Fig.3 Feature point detection on LiDAR-Optical images

(2)梯度方向修改：多模态图像之间往往存在非线性强度差异，会出现梯度反转现象。因此，对SIFT算法的梯度方向进行了修改，将方向限制在区间[0,180°)，公式如下

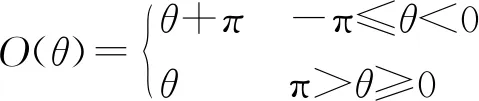
(8)

(9)

基于以上改进，可以提高SIFT算法在多模态图像配准上的正确匹配率。如图4所示，改进的SIFT算法够提供多于4个对应点，确定投影变换参数。

图4 用改进的SIFT算法提取的对应点Fig.4 Corresponding points extracted with the improved SIFT algorithm

1.2 精配准

本节详细描述了特征描述符和相似度准则的构建。精配准阶段主要包括以下6个步骤：

(1)在预配准参考图上采用块Harris算子提取特征点。

(2)计算预配准后参考图和待配准图的结构张量。

(3)采用一种各向异性滤波器来增强结构张量并计算张量方向图。

(4)根据特征点坐标，在张量方向图上分别确定模板窗口和搜索区域。

(5)利用相似度准则，将模板窗口与搜索区域内候选窗口进行比较，确定对应点的位置。

(6)利用步骤(5)所确定的对应点计算转换参数，对图像进行变换。

1.2.1 特征点检测

在参考图中使用块Harris算子获得均匀分布的特征点。先将参考图像分成n×n的不重叠的块，计算图像块中每个像素的Harris值。然后，将每一块中像素点的Harris值从高到低排列，取出得分最高的k个点作为特征点。整幅参考图像上提取n×n×k个特征点，在待配准图像上可以找到n×n×k个大致对应的点。在本文实验中，采用n=5,k=8的参数设置。

1.2.2 密集描述符构建

在本节中，通过各向异性结构张量构建特征描述符，具体步骤如下。

(1)计算张量。张量表示图像边缘的大小和方向信息，虽然边缘的大小会因对比度变化而改变，但随着光照或对比度改变，方向保持不变，所以利用张量提取图像结构信息。经典结构张量表达式为

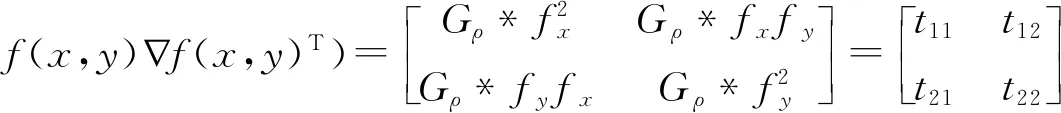
(10)

式中，Gρ是标准差为ρ的高斯核函数；f为强度图像；fx和fy分别表示x方向和y方向的梯度；符号*表示卷积操作；符号∇是梯度算子；上标T表示转置操作。

(2)计算各向异性滤波器。虽然经典结构张量在一些图像处理领域(如：光流估计和纹理分析[23])已经证明了它的价值，但是它也有一些缺点。经典结构张量采用高斯卷积的方法平均邻域内的信息，会导致结构的模糊和错位，因此，它不能广泛用于各种不同的数据[24]。本文采用文献[25]中提出的一种沙漏状的滤波器来避免不必要的模糊

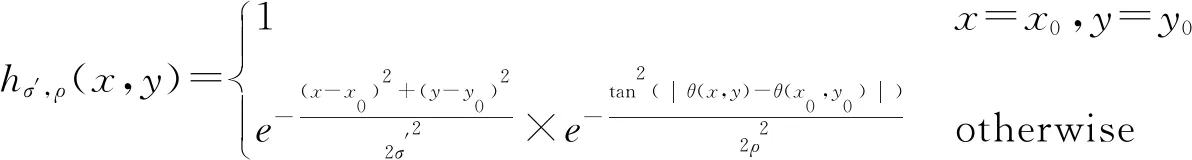
(11)

式中，σ′表示高斯核的尺度，可以决定有效邻域大小；ρ决定方向的强度，一般取值在[0.3,0.7]之间，下面试验中ρ=0.7，(x,y)是有效邻域内点的坐标；(x0,y0)代表有效邻域中点的坐标。式(11)可以分成两部分，左边部分就是高斯滤波器，右边部分则是沙漏状滤波器，图5是不同ρ值下的沙漏状滤波器。

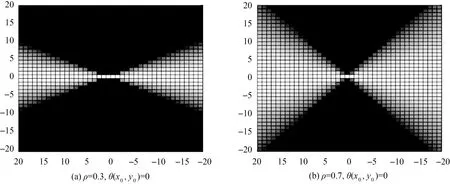
图5 沙漏状滤波器Fig.5 Hourglass filter

式(11)所定义的滤波器是随局部边缘方向θ(x0,y0)进行旋转的，文献[18]中简单的采用梯度方向来表示局部边缘方向，当图像的信噪比较低，其派生的局部梯度向量有噪声时，就会出现问题[26]。张量方向能够捕捉更细微的结构，本文采用张量方向来表示局部边缘方向，计算公式如下

(12)

(13)

(3)计算各向异性结构张量。本文采用式(11)所描述的滤波器对结构张量进行处理，采用类似空洞卷积的方法，如图7(b)所示，比图7(a)展示的传统的滤波器卷积过程更具有计算效率。通过该方法得到各向异性结构张量，公式如下

(14)

式中，H表示有效邻域，分别以一定的间隔来取x和y。

图6 张量方向与梯度方向对比Fig.6 Comparison between tensor orientation and gradient orientation

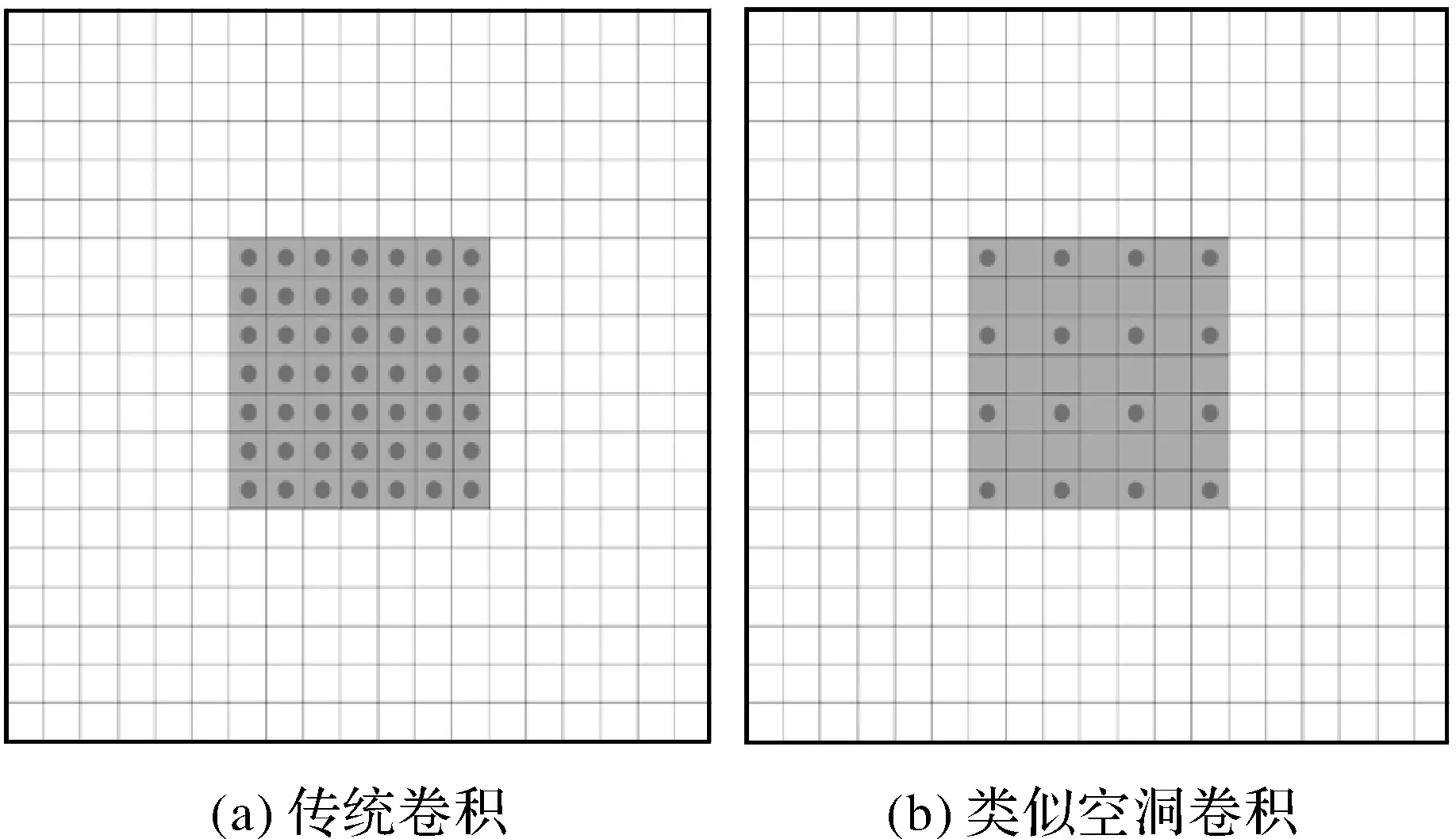
图7 卷积方法Fig.7 Convolution method

利用式(14)得到各向异性结构张量，计算出各向异性张量方向θ′，公式如下

(15)

为了计算效率，使用式(16)代替式(15)计算各向异性张量方向θ′，公式如下

(16)

1.2.3 搜索策略

在得到张量方向图之后，便可以进行模板匹配处理。传统的全局搜索方式计算效率太低。因此，本文采用文献[1—2]中提出的快速模板搜索策略。即以参考图的张量方向图上特征点为中心取w×w大小的模板窗口，在待配准图的张量方向图以粗略对应点为中心取(w+20)×(w+20)大小的搜索窗口。

1.2.4 相似度准则

在南极，科考人员可以登上大陆，而北极到处是浮冰，科考人员需要一直住在船上，所以“雪龙号”上的生活设施也十分完备，游泳池、图书馆、健身房、篮球场、洗衣房、诊疗室、手术室等一应俱全。

多模态图像间存在方向反转，文献[18]发现即使方向反转，但方向间的平行度和垂直度是不变的，提出了一种利用方向平行度的方法。同时受文献[16]启发，本文基于方向平行度，结合梯度互信息，提出了TOMI。该相似度准则综合考虑了图像梯度分布和结构方向，可以更好地保存图像的结构信息，对于多模态影像具有较好的稳健性。

张量方向平行度准则如图8所示，计算如下

(17)

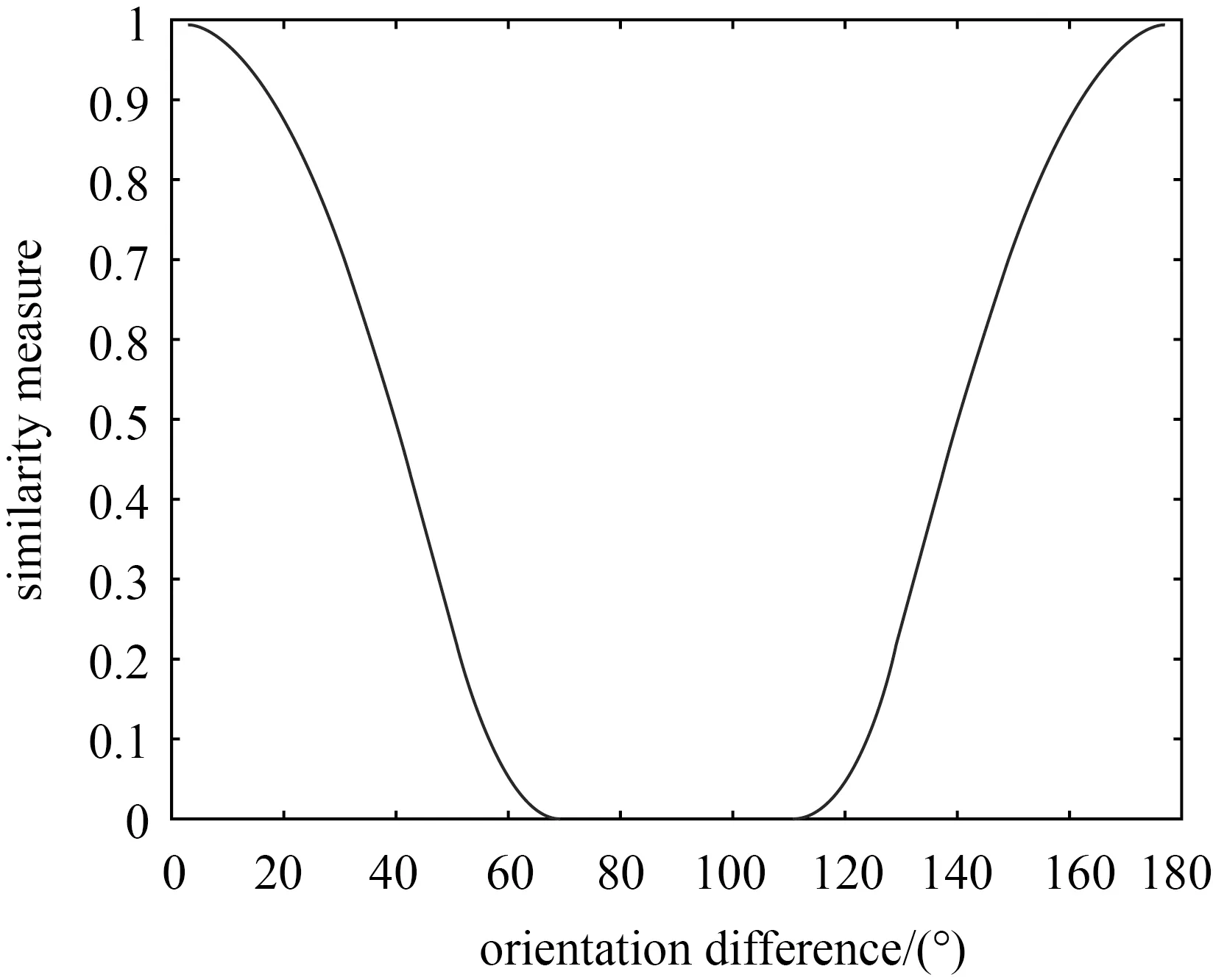
图8 方向平行度曲线Fig.8 Orientation parallelism curve

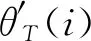
互信息作为一种相似度准则，可以用熵表示，熵的定义如下

(18)

(19)

式中，H(Tg)是Tg的熵；Tg和Cg分别表示模板窗口T和候选窗口C的梯度幅值；H(Tg,Cg)是Tg和Cg的联合熵；pTg(t)是边缘概率质量函数(probability mass function)；pTg,Cg(t,c)是联合概率质量函数。本文采用归一化梯度互信息，公式如下

(20)

结合图像梯度分布和张量方向，TOMI相似度准则公式如下

TOMI(T,C)=S(T,C)×I(T,C)

(21)

(22)

式中，Uc为搜索区域中的所有候选窗口。

为了说明TOMI在多模态图像匹配方面的优势，将其与STV[18]、HOPC、MI、NCC 4种方法通过相似度曲面进行对比，结果如图9所示。测试中使用了两对高分辨率的图像 (Optical-SAR和LiDAR-Optical)，图像之间存在非常明显的非线性强度差异，模板大小均采用65×65像素。图9中，虚线矩形框代表的是搜索区域，实线矩形框代表与模板匹配的目标窗口，相似度曲面的中心对应正确的匹配位置。

图9显示了这些模板匹配方法的相似度曲面。可以明显看出，在Optical-SAR图像对进行测试时，5种方法都能找到正确匹配，不过HOPC、MI和NCC的相似度曲面中均出现了多个峰值，这会对匹配结果产生干扰，只有STV和TOMI是单峰值。对比STV和TOMI两种方法的相似度曲面，TOMI的更显著。在LiDAR-Optical图像对进行测试时，尽管5种方法均能找到正确匹配，不过TOMI和MI表现更好，全局最大值显著。这初步证明了本文提出的相似度准则在多模态图像配准上具有更强的稳健性。

2 本文试验

首先评估预配准算法与精配准算法在多模态图像上的匹配性能，将精配准算法与其他多模态图像匹配算法进行比较分析。然后，讨论本文算法对噪声的稳健性强弱以及模板大小对匹配性能的影响。本节对算法精度的评估采用两种方法：①对棋盘图和放大子图进行目视检查；②采用均方根误差(root mean square error,RMSE)和正确匹配率(correct matching rate,CMR)这两种量化准则对配准结果进行评估。

2.1 数据集

利用5组多模态图像评价本文提出算法的有效性。这5组图像被分成4类：① Visible-Infrared；② LiDAR-Visible；③ Optical-SAR；④ Map-Optical。这5组图像对之间均存在明显的非线性强度差异，包括低分图像(240 m)和多种高分图像(0.5～3 m)，覆盖了包括结构信息丰富的城市区域，以及结构信息缺乏的山川湖泊，甚至还有云雾干扰。表1给出了测试数据的信息。

表1 测试数据描述Tab.1 Descriptions of the test data

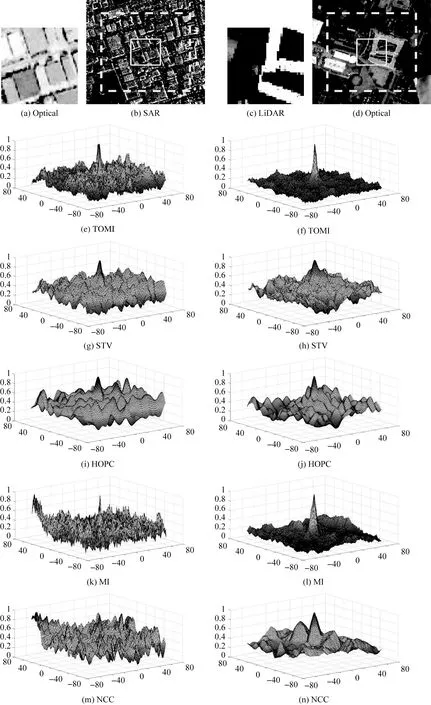
图9 相似度曲面Fig.9 Similarity surface

(1)Visible-Infrared：选用了2对Visible-Infrared图像对进行试验：①城市区域的高分图像，具有丰富的结构和边缘信息；②低分图像，该图像对被云雾遮挡，并且时态相差一年以上，具有显著的非线性强度差异，对配准很具有挑战性。

(2)LiDAR-Visible：选用一对城区LiDAR-Visible图像对，从2幅图像的强度特征上可以看到很大的差异。此外，LiDAR强度图受噪声影响，导致图像退化，给配准增加了困难。

(3)Optical-SAR：选用一对覆盖城区的高分图像，图像对中存在非常丰富的结构信息。不过，城区有高层建筑，局部畸变明显。同时，SAR图像存在严重的散斑噪声影响，图像中的精细结构被散斑噪声破坏，使得配准较为困难。

(4)Map-Optical：这对图像的强度差异十分显著，包含的纹理信息很少。并且，地图上标注一些文字，这些给配准带来了挑战。

2.2 预配准试验

遥感图像之间的旋转和尺度差异是影响配准精度的主要因素。上述的试验数据没有显著的旋转和尺度差异，为了验证预配准算法对于图像旋转、尺度差异的稳健性，进行了模拟试验。将上述试验数据case 1—case 5中的待配准图像先分别采用θ=[10°,20°,30°]进行旋转，再分别对旋转后的图像采用比例因子s=[0.9,0.8,0.7]进行缩小，以此模拟图像对之间的旋转、尺度差异。

由图10可以看出，随着角度、尺度差异的增大，预配准算法找到的对应点的数量逐渐减少。不过，预配准算法始终能找出足够多的对应点 (大于4个对应点)，让图像可以进行投影变换，对齐图像对。

图10 不同角度、不同尺度下的多模态图像中的对应点Fig.10 Corresponding points of multi-modal images at different angles and scales

本文采用RMSE和CMR对预配准进行定量化评价。对于预配准而言，点位误差小于3个像素视为正确匹配。

表2 预配准精度评定 (RMSE,CMR)Tab.2 Accuracy evaluation of pre-registration(RMSE,CMR)

由表2中可以看出，预配准在处理case 1和case 2中的Visible-Infrared图像对时具有较好的配准效果，能够抵抗多模态图像中的非线性强度差异。在case 3—case 5中，图像对受噪声影响，RMSE较大，但是都在10个像素以内，可以大致对齐具有旋转和尺度差异的多模态图像。

2.3 精配准试验

在精配准阶段，本文先用目视检查对算法进行评估。精配准采用32×32像素的模板大小，得到测试数据的棋盘图，可以直观地看出精配准的配准效果(如图11所示)。图11中，对比预配准与精配准的棋盘图可以看出，预配准已经将参考图和待配准图大致对齐。不过从放大子图可以看出，预配准之后还有一些局部区域没有对齐。而精配准处理后，没对齐的区域都已经精确对齐。

目视检查之后，再对精配准算法进行量化评价，将对应点的点位误差小于1个像素视为正确匹配。精配准算法作为一种模板匹配方法，将它与最先进的模板匹配算法(STV、HOPC、MI和NCC)进行比较，来验证其多模态图像匹配的能力。其中STV和HOPC都是利用结构信息来进行模板匹配，且取得了较好地配准效果。MI和NCC是基于强度的经典模板匹配方法。

(1)STV提出了一种基于结构张量投票方案的密集特征描述子，能够很好地抵抗由于强度畸变引起的梯度反转现象，对多模态图像间存在的非线性强度畸变具有较好的稳健性。

(2)HOPC扩展相位一致性模型以建立其方向信息，构建了一个密集描述子，能够捕捉图像的几何结构和形状特征，在多模态图像配准上取得了较好的效果。

(3)MI模板匹配算法基于互信息的最大化，对非线性强度差异具有较好的稳健性。不过，MI对直方图bin的大小很敏感，将直方图bin设置为32，在数据集上取得最佳的匹配性能。

(4)NCC是一种常用的图像匹配算法的相似度准则，它不受线性强度变化的影响。

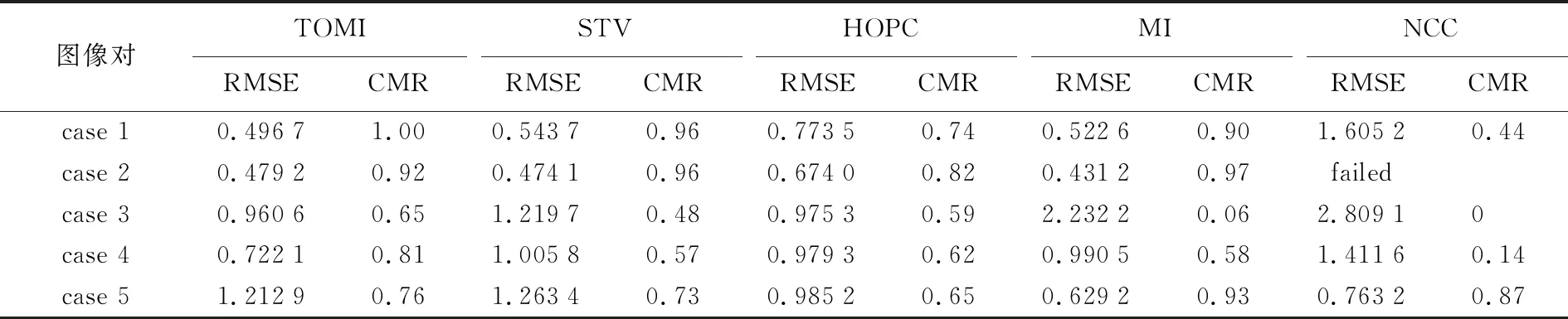
表3 精配准精度评定(RMSE,CMR)Tab.3 Accuracy evaluation of fine registration(RMSE,CMR)

从表3可以看出，在case 1中，图像之间存在梯度反转现象，TOMI和STV利用张量方向平行度可以很好地处理梯度反转。TOMI该图像对上的配准效果最佳，其次是STV、MI、HOPC及NCC，显示出TOMI在表达结构这方面的优势。在case 2中，这对低分图像包含纹理信息较少，故TOMI的配准效果稍微逊色于MI。由于NCC对线性辐射差异具有不变性，不能很好地处理图像间复杂的强度变化，所以NCC在该图像对上配准失败。在case 3中，LiDAR-Visible图像对之间存在噪声影响以及非常显著的强度差异。TOMI表现最好，只有TOMI和HOPC能达到亚像素精度，明显优于其他3种算法，STV其次，而MI和NCC在该图像对上配准效果很差。因为测试的图像对之间存在非常丰富的结构信息，使得3种基于结构的方法(TOMI、STV、HOPC)在匹配性能上优于两种基于强度的方法(MI、NCC)。在case 4中，是一对城区的Optical-SAR图像对。TOMI配准精度和正确匹配率都是最高的，原因是TOMI具有良好的噪声稳健性，可以很好地抵抗SAR图像上存在的散斑噪声的影响。同时图像对中存在非常丰富的几何结构和轮廓信息(如建筑和道路)，使得TOMI可以很轻易捕捉到这些结构信息来找对应点。在case 5中，Map-Optical图像对之间除了边界几乎没有任何共享的特征，使得TOMI、STV和HOPC的配准精度低于MI和NCC。综合而言，相比较其他4种算法，TOMI算法结合图像的统计特性与纹理特征，在结构表达方面更具有优势，更能适应非线性强度变化，对图像噪声具有更好的稳健性，取得了最好的配准效果。

图11 预配准与精配准对比Fig.11 Comparison of pre-registration and fine registration

2.4 噪声稳健性试验

检验所提出的相似度准则对噪声的稳健性，在case 1的图像对上进行模拟试验。通过给图像对添加均值为0，方差为v=[0.1%,0.2%,…,1%]的高斯噪声重复进行5次，生成5组噪声图像。用噪声图像的平均正确匹配率来对TOMI、STV、HOPC、MI和NCC算法的噪声稳健性进行评价。算法模板大小都选用64×64像素，对应点的点位误差小于1个像素视为正确匹配。

图12展示了5种模板匹配算法随噪声等级提高，平均正确匹配率的变化。在增加噪声的条件下，TOMI在5种算法中表现最优，平均正确匹配率一直是最高的，其次是STV、MI、HOPC和NCC。多模态图像往往带有大量的噪声，TOMI能够很好地适应噪声引起的图像退化。对比基于结构张量的模板匹配算法，TOMI稳健性优于STV，因为STV是基于梯度方向构建各向异性滤波，而TOMI是基于张量方向构建各向异性滤波。张量方向比梯度方向对噪声更具有稳健性，且能够描述更细微的结构变化。同时，TOMI不仅利用方向平行度，还利用梯度分布构建相似度准则，进一步增加了算法的稳健性。

2.5 模板大小分析试验

验证所提出的算法在不同模板大小下的匹配性能。将5种模板匹配算法在case 1—case 5中的多模态图像上进行试验，取5对图像的平均正确匹配率作为评价指标，模板大小取[32,40,…,112]，对应点的点位误差小于1个像素视为正确匹配。

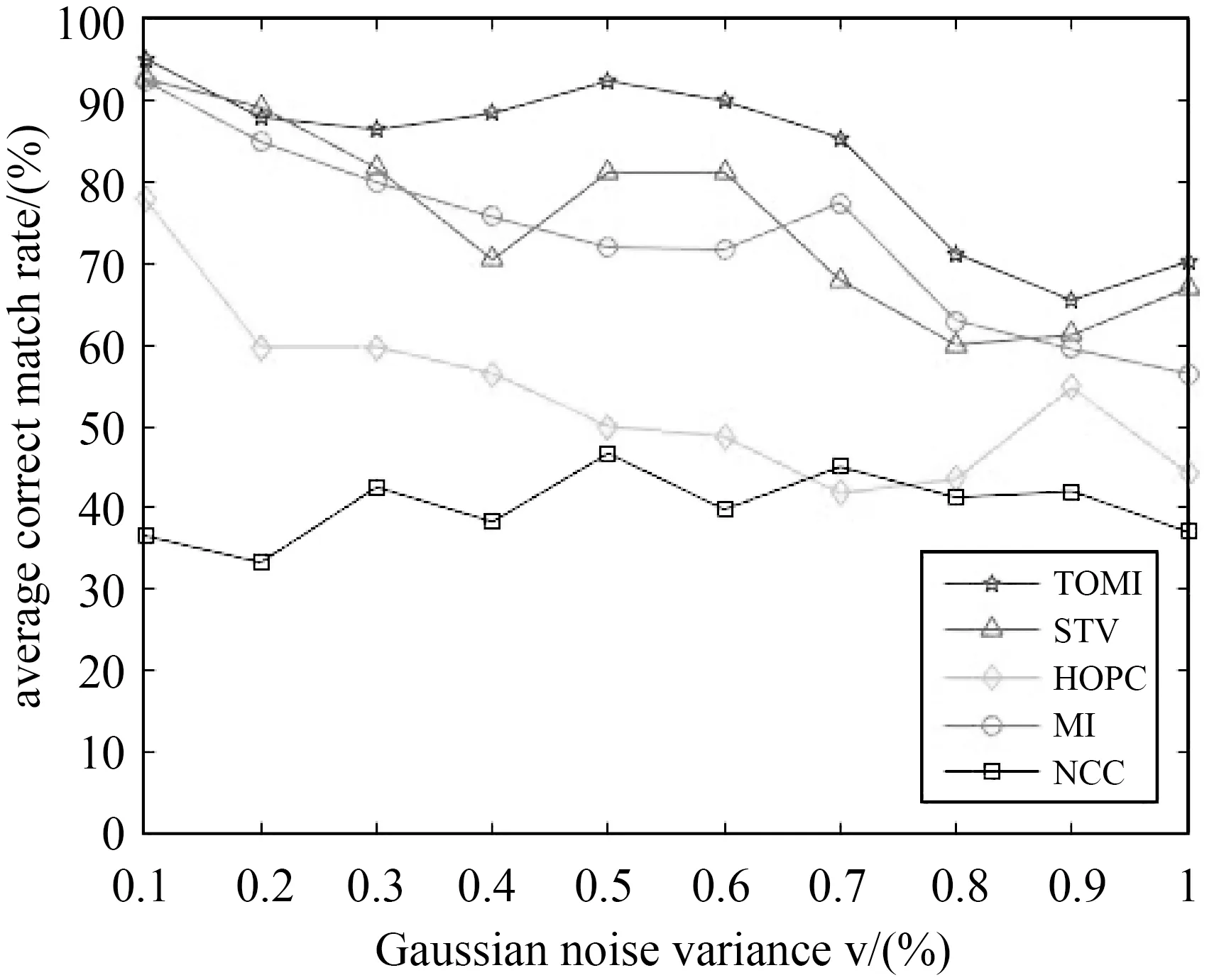
图12 相似度准则在各种高斯噪声上的平均正确匹配率Fig.12 Average matching correct rates of similarity measures over the various Gaussian noise

图13显示了不同模板大小下，5种模板匹配方法在case 1—case 5图像对上的平均正确匹配率对比结果。在5种模板匹配算法中，本文提出的TOMI算法在不同模板大小下实现了最高的匹配精度，这说明了TOMI对多模态图像匹配的优越性。NCC的性能最差，不能很好地处理图像间复杂的强度变化。对一些强度变化剧烈的图像对(如Visible-Infrared)甚至会出现配准失败的情况。尽管MI的表现比NCC好，不过它不能有效地处理这些多模态图像的匹配，由表3可知，MI在case 3中表现不佳，不适合处理非线性强度变化和噪声影响下的LiDAR-Visible图像对。HOPC配准平均正确匹配率优于MI，在各个模态图像配准时都取得较好的表现，总体表现要优于MI。不过，HOPC的配准效果还是低于TOMI和STV，这是因为HOPC使用拓展的PC来提取图像结构信息，尽管PC可以抵抗光照和对比度的变化，但是PC图所含有的信息太少，PC图上的大部分像素值都接近于0。此外，PC图包含边缘信息受噪声影响，会导致特征描述不准确，对特征的描述不够稳健。

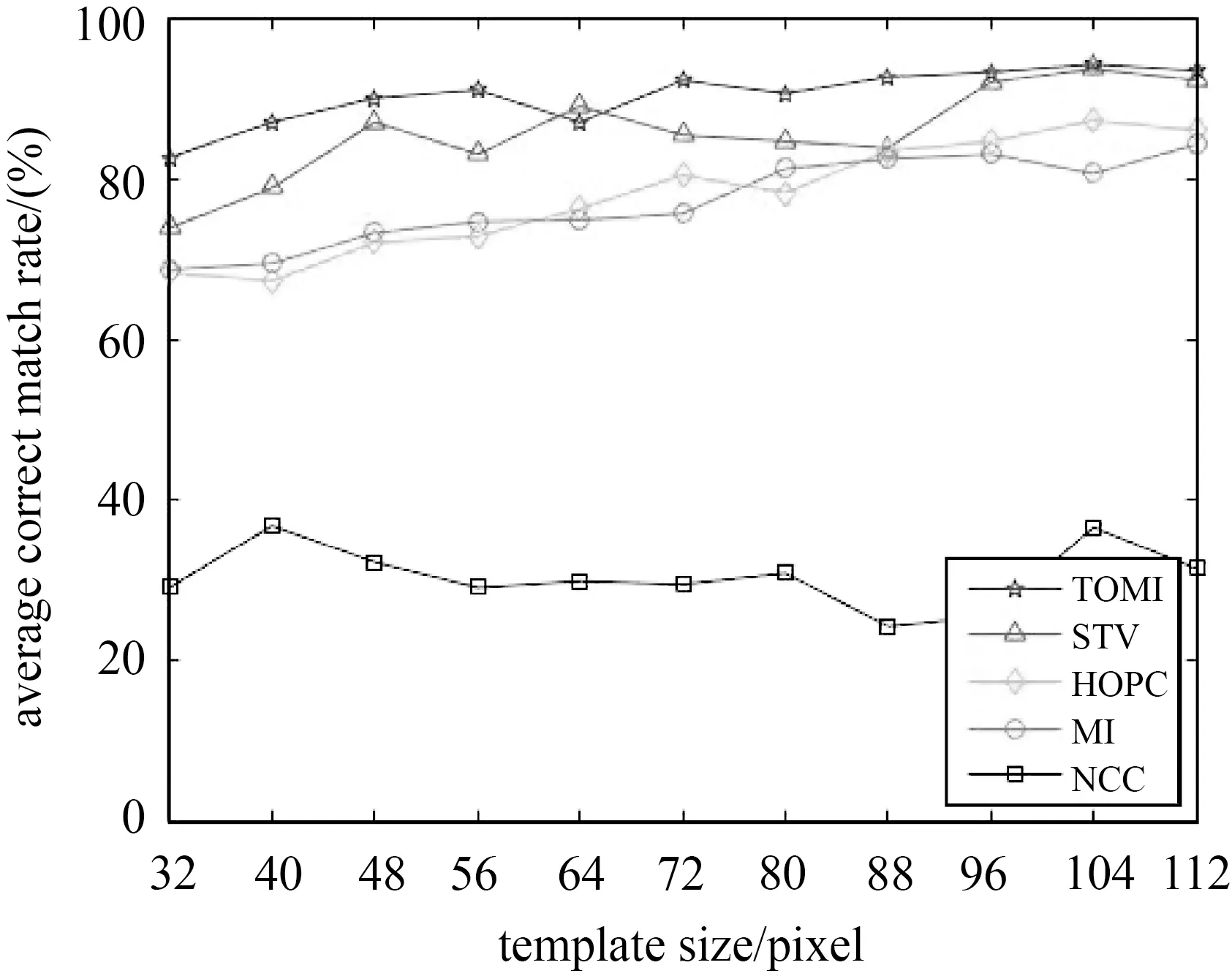
图13 不同模板大小的平均正确匹配率Fig.13 Average matching correct rates of investigated algorithms over template size

3 结 论

本文提出了一种多模态图像配准方法，以解决显著的非线性强度差异和噪声退化问题。在预配准阶段，对SIFT算法进行改进，粗略对齐多模态图像对。在精配准阶段，用各向异性结构张量来捕捉图像几何结构，大大降低了多模态图像间噪声的影响，可以更可靠地表现真实数据，同时对非线性强度差异有较好的稳健性。更进一步，将张量方向平行度与梯度互信息相结合，提出了TOMI相似度准则，利用图像统计特性与纹理特征，进一步提高算法对图像噪声的稳健性，增强了算法的匹配性能。试验结果表明，TOMI在配准精度上和对噪声的稳健性上均优于STV、HOPC、MI和NCC等先进的图像匹配方法。

然而，本文提出的算法仍然有一些局限性。通过试验发现，如果图像中包含的结构或形状信息较少，TOMI的性能会降低。在精配准试验中，TOMI在case 1—case 4中均取得亚像素级的配准精度，而在case 5这对纹理信息缺乏的图像对中，RMSE降低至像素级。此外，发现其余两种基于结构的算法STV与HOPC在该图像对中配准精度也在像素级，明显低于基于强度的配准算法MI与NCC。因此，在下一步的研究中，可以更深入地结合MI或NCC这类基于强度的配准方法，增强算法在纹理缺乏地区的配准效果。