洪水基流分割非参数检验方法优选
冷梦辉,白 桦,李二辉,向君正,黄监初,桂发亮
(1.南昌工程学院江西省水文水资源与水环境重点实验室,江西 南昌 330099;2.江西省宜春水文局,江西 宜春 336000)
基流是源于包气带水和地下水的慢速径流,对行业供水、防汛抗旱及生态环境保护等具有重要价值[1-2]。海绵城市建设核心控制目标包括水资源、水环境、水生态、水安全等,基流分割模拟、预测预报、规划管理是目标达成的关键[3]。目前,常用基流分割方法有图解法、数值模拟法、水量平衡法、同位素法和水化学法等[4]。不同基流分割方法适用范围不同,往往使基流分割结果差异较大[5-6],加之气候变化和人类活动的影响,基流分割难度加大,现有基流分割方法难以准确甄别变化环境下流域径流成分[7-8]。流域退水过程径流成分较为复杂,包含饱和地表径流、直接地表径流、壤中流、地下径流等,对气候变化和人类活动有一定响应[9],变化环境下退水过程径流成分相互转换,导致径流成分、组分和水文情势发生改变,各径流成分间流速差异较大,可能存在多个突变点[10-12]。而变化环境下径流成分转换过程中,现有基流分割方法可能存在一定的不确定性。对于环境变化剧烈的海绵城市来讲,绿色屋顶、生物滞留池、下沉式绿地和透水铺装等海绵设施增大了地表稳渗率和糙率,更多地表水进入地下,同样也导致流域径流成分、组分及比例发生明显变化,退水过程相应存在突变点。目前,采用数值模拟方法简化基流分割过程是最常用的基流分割方法[13-15],但主要用于处理长序列的水文动态数据,不适宜针对单场次洪水基流分割。采用非参数水文序列突变检验法对场次洪水基流分割的研究较少,而非参数突变检验法具有高效、准确的特点,对检验过程变化速率较为敏感,能准确识别过程变化中的突变[16]。
本文以江西省萍乡市海绵城市建设示范区为研究对象,基于五丰水文站2016—2018年实测场次洪水数据,采用累积距平法、Pettitt法、滑动T检验法和Mann-Kendall检验法划分场次暴雨洪水径流,以直线斜割法所得基流流量为据,借助集对分析法优选非参数检验方法,以期为海绵城市洪水基流分割模拟、预测预报及规划管理提供参考。
1 研究区概况
本文所用数据为江西省萍乡市五丰河流域五丰水文站2016—2018年实测场次洪水数据。
2 研究方法
2.1 标准退水曲线
基于五丰河流域2016—2018年实测场次洪水流量数据,借助AutoCAD软件分别绘制逐年场次洪水流量过程线,将各年洪水流量过程线按同一比例沿时间坐标轴平移使其尾部重合,分别绘制各年光滑下包线,即为流域逐年标准退水曲线;作一斜线使斜线和该年标准退水曲线分别与时间坐标轴所围面积相等,用该斜线描述各年标准退水曲线时程倾向率,即为标准退水等效曲线;以逐年光滑下包线为据,采用直线斜割法划分各年场次洪水径流成分,可得场次洪水基流分割点及相应地下径流起始流量。
2.2 场次洪水径流分割
鉴于场次实测数据时间间隔各有差异,本研究以0.5 h为时间间隔,采用线性内插法进行数据扩充,计算场次洪水流量间斜率;借助非参数突变检验法识别场次洪水流量斜率突变来划分场次洪水径流,识别场次洪水基流分割点,即为地下水退水起始流量;以直线斜割法所得基流流量为依据,运用平均相对误差法[18]对比分析各非参数检验法所得基流流量,并评价各非参数检验法准确性。筛选国内外较为常用的突变点检验方法,本文主要运用累积距平法、Pettitt法、滑动T检验法和Mann-Kendall检验法4种较为经典的非参数突变检验法来检验五丰水文站各场次洪水流量过程线中斜率突变点。
2.2.1累积距平法
累积距平法主要以离散数据对其均值的离散程度为依据,通过辨别累积距平曲线的上下起伏变化来判别样本点某一时间点处发生突变的均值检验方法,若累积距平值增大,表明离散数据大于其均值,反之则小于其均值[19-20]。差积曲线上的拐点即为突变点,反映在雨洪过程线上则为地表径流与地下径流的分割点。
(1)

2.2.2Pettitt法
在相互关系上,要突出“预备役”和“部队”特色,妥善处理与现役部队和民兵组织的关系,既要防止“现役有啥我有啥”的重复建设,也要防止“现役裁啥我裁啥”的跟风现象;对于一些未来战争还可能用得上的“传统型”预备役部队,现役部队裁减了,反而需要以预备役形式来保留,而不能一味与现役部队比“高、精、尖”。
Pettitt法是识别水文序列突变点的非参数检验方法,其假设样本容量中存在突变点m,突变时刻tp,采用Mann-Whitney的统计量Utp,n检验样本序列突变点前后两个子样本{x1、x2、…、xtp}和{xtp+1、xtp+2、…、xn}二者间累积分布是否存在显著差异[21-22]。统计量Utp,n计算公式为
(2)
(3)
(4)
式中:xtp、xi分别为第tp、i时刻场次洪水退水流量斜率值;K为tp时刻出现Utp,n最大统计量;若概率P≤0.05,则m点为显著突变点。
2.2.3滑动T检验法
滑动T检验法主要检验由两子样本序列的均值是否存在显著差异来辨别突变点[23]。假设在连续序列中存在一个突变点,突变点前后两段子序列的容量分别为n1、n2,计算统计量s:
(5)

2.2.4Mann-Kendall检验法
Mann-Kendall检验法目前广泛用于降水、径流等时间序列的非参数趋势检验或突变检验[24-26]。对场次洪水流量消退相邻时段斜率样本容量为n的时间序列x,将第i个样本xi>xj的累计数统计成为Fk:
(6)
式中:fi为前后两个样本的值,分别取0和1。
2.3 基流分割方法优选
基于2016—2018年场次洪水直线斜割法和各非参数突变检验法所得基流分割流量数据,采用集对分析法将各场次洪水直线斜割法识别的基流分割点流量定义为集合Y,即Y={y1,y2,…,y16},将各非参数突变检验法即累积距平法、Pettitt法、滑动T检验法和Mann-Kendall突变检验法,识别的各场次基流分割点流量定义为集合X={x1,x2,x3,x4},组成集对。通过参考相关文献[27-28],考虑本文实际数值情况制定分类标准为:若各场次洪水基流流量Yi(i=1,2,…,16)在±10%内,则为同一特性,将该指标归为第Ⅰ类;若Yi在±10%~±20%之间,则为差异特性,将该指标归为第Ⅱ类;若Yi在±20%之外,则为对立特性,将该指标归为第Ⅲ类。根据分类原则和联系数最大原则统计联系方程中的联系系数,计算各非参数检验法集对分析联系度。集对分析是一种新的处理不确定性问题的理论与方法,反映两个样本间共有、对立及差异的特性,通常用联系度μ描述两集合样本的相关程度[28]:
μ=a+bI+cJ
(7)

式中:N为集合样本特性总数;S为集合样本中同一特性个数;F为集合样本中差异特性个数;P为集合样本中对立特性个数;I为差异不确定系数;J为对立系数且J=-1;a为集合样本同一度;b为集合样本差异度;c为集合样本对立度,且满足a+b+c=1。
3 结果与分析
3.1 标准退水曲线及基流分割点
图1为五丰河流域2016—2018年标准退水曲线。分析可知:2016—2018年标准退水曲线洪峰流量Q分别为22.9 m3/s、15.4 m3/s和20.8 m3/s,基流分割点时间分别在31.9 h、19.3 h和7.9 h,相应流量分别为4.63 m3/s、6.29 m3/s和7.65 m3/s,退水流量时程倾向率分别为0.05 m3/(s·h)、0.04 m3/(s·h)和 0.02 m3/(s·h)。其中,2016年标准退水曲线地表径流量、地下径流量分别为92.7万m3和45.5万m3,占径流总量比例分别为67%和33%;2017年标准退水曲线地表径流量、地下径流量分别为67.7万m3和 65.8万m3,占径流总量比例分别为50.7%和49.3%;2018年标准退水曲线地表径流量、地下径流量分别为 10.9万m3和67万m3,占径流总量比例分别为14%和86%,表明流域洪峰流量、洪水总量相对2016年均减少,退水速率减缓,地表径流量占径流总量比例减少,地下径流量占径流总量比例增加。采用直线斜割法识别出各场次洪水基流分割点(图1),分析可知:2016—2018年场次洪水基流分割点处流量分别在0.85~6.5 m3/s、3.65~9.45 m3/s 和1.29~4.18 m3/s间变化,均值分别为2.35 m3/s、6.26 m3/s和2.59 m3/s,变差系数分别为0.75、0.35和0.40,2018年场次基流分割点处流量年均值相对2016年增大了10.0%,变差系数相对2016年减小了45.9%,表明场次基流分割点处流量均值相对2016年增大,异质性变小。
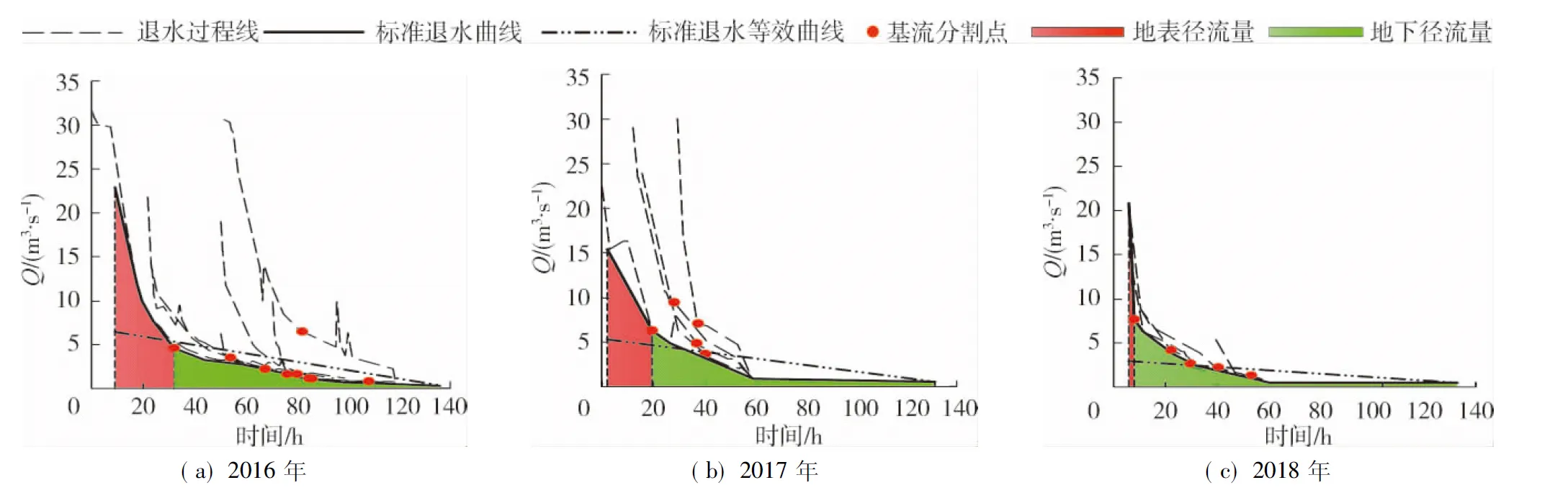
图1 逐年标准退水曲线及直线斜割法识别的基流分割点
分析海绵城市建设前后流域退水规律变化成因可知:海绵城市源头削减[29]功能固持水量,使流域径流系数减小、稳渗率增大,地下径流量占径流总量比例提升,弥补径流系数减小导致径流总量削减效应,造成地下径流量增大47.3%[30-31];过程阻滞和末端调蓄措施增大地表粗糙度,发挥蓄洪、滞洪、错洪功能,造成流域地表汇流速率降低60%,汇流过程减缓,洪水过程“坦化”[32-33];以经典防洪排涝工程为代表的灰色基础设施可影响流域基流[34-37],造成地下水增加[38-39]。
3.2 基于非参数检验的场次洪水基流分割点
基于五丰水文站2016—2018年场次洪水退水过程,以直线斜割法所得基流流量为据,采用非参数检验法识别洪水基流分割点,结果见图2(白圈为直线斜割法划分第I类标准);以直线斜割法所得基流流量为据,对比累积距平法、Pettitt法、Mann-Kendall检验法和滑动T检验法所得基流流量见表1。其中,Mann-Kendall检验法在显著水平α=0.05无统计意义突变点,即Mann-Kendall检验法未检验出场次洪水基流分割点。分析表明:2016年、2017年和2018年与直线斜割法所得基流流量最接近的非参数检验方法是Pettitt法,其中2016年相应基流流量年均值分别为2.35 m3/s和2.42 m3/s,相对误差为3%,基流流量变差系数Cv分别为0.75和0.74,相对误差为1%;2017年基流流量年均值分别为 6.26 m3/s 和6.24 m3/s,相对误差为0,基流流量变差系数Cv分别为0.35和0.39,相对误差为11%;2018年基流流量年均值分别为2.59 m3/s和 2.55 m3/s,相对误差为2%,变差系数Cv分别为0.40和0.39,相对误差为3%。

图2 非参数检验法识别的基流分割点

表1 不同径流分割法基流流量统计结果
Pettitt法所得2016年、2017年和2018年突变点相对出现时间分别在11.3~72 h、8~37 h和8~28 h间变化,均值分别为37.1 h、21.1 h和18.9 h;地下径流历时占洪水历时比例分别为47%、56.1%和52.1%。结果表明,随着海绵城市建设,年均地下水退水起始流量增大、地下水退水时间提前,与赵刚等[40]研究结果一致。究其原因,海绵设施发挥源头削减、过程阻滞和末端调蓄功能,使更多坡面洪水阻滞并渗入地下,直接地表径流结束时间提前,地下径流历时占洪水历时比例增加,与前文流域退水规律变化归因分析结论一致。
3.3 基于集对分析的基流分割非参数检验方法优选
基于2016—2018年直线斜割法所得场次洪水基流流量数据,设计集对分类标准划分场次洪水基流流量分类范围,依据分类范围统计各非参数检验法集对分析联系度,结果见表2。分析可知:Pettitt法联系度最大,为0.81;滑动T检验法联系度次之,为0.5;Mann-Kendall检验法联系度最小,为-1。可见,Pettitt法与直线斜割法所得基流流量相似性最大,是城镇洪水基流分割非参数检验的适宜方法。究其原因,城镇洪水退水过程主要径流为直接地表径流和地下径流,两径流流速差异较大,退水速率明显不同,其退水过程相应存在径流分割点。

表2 场次洪水基流流量集对符号量化及联系度
本文主要采用累积距平法、Pettitt检验法、滑动T检验法和Mann-Kendall检验法识别城镇化流域退水过程地表径流和地下径流的突变点,其中,累积距平法和滑动T检验法检验时序数据时均有累加过程,数据有明显阶段性变化特征,易使突变点数值均化,造成突变点识别产生误差;Mann-Kendall检验法检验均值、方差或均值与方差组合突变,退水过程检验出多个突变点,不适宜检验仅由直接地表径流和地下径流组成的城镇化流域退水过程;Pettitt法对过程变化速率敏感,专注检验一个突变点,适用性较好,易于区分直接地表径流和地下径流分割点,适用于城镇化流域地表和地下径流的分割。
4 结 论
a.以直线斜割法为准,Pettitt法相较累积距平法、滑动T检验法、Mann-Kendall检验法所求年均地下水退水起始流量相对误差最小,为1.6%;地下水退水起始流量年均变差系数相对误差亦最小,为5.1%。Pettitt法与直线斜割法所求地下水退水起始流量最接近。
b.集对分析优选结果表明,Pettitt法是最适合检验城镇化流域洪水基流分割点的非参数检验法,滑动T检验法次之,累积距平法与Mann-Kendall检验法效果最差。
c.海绵城市建设后洪水退水速率减缓,洪峰流量、洪水总量减少,地下径流量占径流总量比例增大,年均地下水退水起始流量增大、地下水退水时间提前。随着海绵城市建设规模化后,天然、人工海绵体将充分发挥积存、渗透、净化和缓释功能,退水过程将由单一地表和地下径流成分向地表径流、壤中流、地下径流等复杂成分转变,基流分割方法适用性将待进一步探讨。

