皖南郎川河流域基流分割
董广博
(合肥工业大学 土木与水利工程学院,安徽 合肥230009)
基流的一般定义为补给多数河流枯水期河川径流的流量,基流也是河流生物维持基本生存的必要条件之一[1],从水文学的角度出发,认定基流为深层地下径流[2],其中地下径流又可分为快速(浅层)和慢速(深层)[3]。近些年,全球的极端天气频繁出现,更使得水资源分配不平衡现象加剧,也使得可用水资源量一再发生变化。安徽南方地区地理环境相对复杂,气候变化较为明显,目前该地区经济发展差异性较大。境内水资源丰富,且主要以山区、丘陵区为主,对过境客水依赖程度高;近些年工农业发展迅速,农业发展的不合理不科学等情况突出,水质污染造成水质性缺水日益严重,水资源形势不容乐观。
为此,本选题以皖南郎川河流域为基础,基于目前相对较为成熟的多种基流分割方法,围绕郎川河流域基流分割后基流指数的稳定性,基流量的演变趋势以及对基流量的验证的结果,比选最优方法,在郎川河流域进行实施。
1 研究方法及数据资料
在基流分割领域,许多专家学者投入大量研究,得出多种较为成熟的基流分割方法。基于对基流的定义存在差异性及基流过程的复杂性,现阶段还没有某一种基流分割方法可以适用于的所有情况,因此针对不同地区选择基流分割方法至关重要。本章节总结目前较为成熟的多种方法,可以根据适用条件比选为郎川河流域基流分割提供依据。
1.1 水量平衡法
水量平衡法主要包括参数分割法和水文模拟法。参数分割法主要包括加里宁法和水库法。加里宁法来源于二十世纪五十年代苏联学者加里宁,二十世纪八十年代,有学者对该方法进行了改进,对改进后的方法进行总结,得出基流估算方程为:

Q下n-1——时刻n-1 的基流量(m3);
Q下n——时刻n 的基流量(m3);
B——比例系数,基流与径流的比值;
α——退水系数,地表水与地下水转换速率。
1.2 时间步长法
时间步长法利用计算机技术研究开发出相应程序,这些年来被广泛采用。运用时间步长法进行基流分割,首先要计算的是直接径流所持续的时间,目前计算该时间采用的是经验公式:

式中:
N——直接径流持续时间长度(d);
A——流域面积(km2);
时间间隔时长益取在3~11d,且应为2N 数值最为接近的奇数。
1.3 基流指数法
基流指数法又称为PART 法。是美国地质调查局提出的基流分割方法,后期设计出计算程序。此种方法主要围绕年内日径流量,基于一次降雨洪峰后期,在消退期进行基流分割。
1.4 平滑最小值法
该方法主要针对全年的日径流量数据组进行处理,将全年365 天按时间间隔划分成N 份,在每个时间间隔365/N 天中确定一个最小的qt组成数列,将每个qt与相邻时间段的最小值(qt-1,qt+1)进行比较,若满足kqt≤min(qt-1,qt+1),则将该点确定为一个节点,重复上文所述比较过程。
1.5 数字滤波法
数字滤波法计算基流分割原理源于信号分析,把径流过程进行处理,转化成数字信号。Lyne 和Hollick 于二十世纪七十年代末期提出Lyne-Hollick 滤波法,于1990 年应用于基流分割。在月径流的基础上,该滤波法可分割出月基流,采用1 次滤波进行滤波参数调试较为合理。
Chapman 在Lyne-Hollick 基础上,提出Chapman 滤波法,其计算公式为:
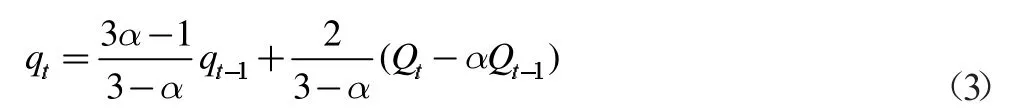
对目前水文工作者主要使用的方法进行统计,包括上文所述几种方法。
2 项目区概况
郎川河流域位于皖南山区,流域内地势高差起伏较大,以山地丘陵为主,域内河道天然冲积形成,河道坡降较大,河槽过流能力比较小。郎川河发源于广德县东南境内的牛山,牛山最高点为661.8m。卢村水库控制流域面积139km2。坝址以上分为东、西两支,东支来水面积为71km2,西支来水面积为68km2,均属高山区。河道两侧两山对峙坡陡流急,河道平均比降东支为10.2‰,西支为8.15‰,最高山峰海拔高程661.8m。
3 郎川河流域河川基流分割及估算
传统的基流分割方法以手工图解法为主,该方法操作复杂、主观性较强,且对于长系列数据处理较麻烦。基于科学技术的进步和水文计算手段的发展,基流分割方法越来越趋于简便快速,现在可利用计算机进行基流分割处理,目前使用较为成熟的方法包括滤波法、水量平衡法、时间步长法等。
目前不同的基流分割方法适用条件区别不够明显,且重合度较高,针对研究较少,数据资料缺乏的区域进行基流分割较为困难,且所得结果准确性无法保证。本文以皖南郎川河流域为例,探讨出适用性与可靠性较高的计算方法,为了解和分析该流域基流的演变提供技术支持。
3.1 基流分割结果分析
根据卢村水库1983-2012 年30 年径流资料,采用数字滤波法(F1、F2、F3、F4)、BFI 法(F、K)、HYSEP 法(FI、SI、LM)、加里宁等四类10 种方法进行基流分割,计算结果见表1。
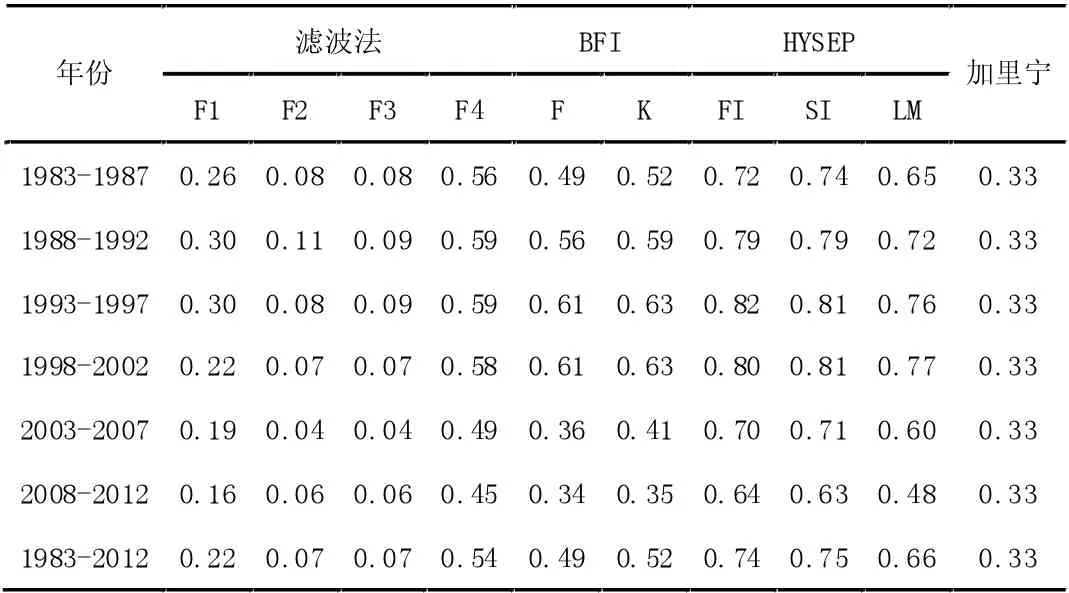
表1 10 基流分割方法估算基流指数
为了进一步研究10 种基流分割结果之间的差异性,进而比选其稳定性,对计算结果进行数理统计计算,结果见表2,由表可知,数字滤波法的F2、F3 法求得极值较大;BFI 两种方法求得极值比基本一致;而数字滤波法F1、F4 法与HYSEP 方法三种方法计算结果的极值比较接近;加里宁法属于经验系数,根据径流量百分比所确定;由此可知数字滤波法F1、F4 法与HYSEP方法三种方法计算结果波动性较小,相较于前几种更为稳定。
3.2 径流过程线研究
采用Nash-Sutcliffe 方法对10 种基流分割方法所得结果进行验证,结果见表3。从表中可知,仅数字滤波法的FI 法,计算结果与实测值基本一致,效率系数为0.7,相对误差为9.33%,根据效率系数与相对误差相关要求对比可得:满足效率系数L 超过0.6,平均相对误差R 小于10%,因此由此可知数字滤波法的FI 法较为合理。
3.3 基流分割方法的验证
根据上文比选结果,郎川河流域基流分割采用数字滤波法F1 法较为合理,由于基流分割方法缺乏严格理论依据,不能排除计算结果的偶然误差,因此基流分割方法的选取必须进行多方论证。本章节根据郎川河流域附近地形、地势、气候条件,选取两个等较为相似区域典型封闭小流域,对所选取基流分割方法进行验证。
选取东津河流域沙埠站和西津河流域胡乐司站水文1968~2010 年水文资料,对年径流数据资料进行排频,选取具有代表性的枯水年、平水年、丰水年,对代表年进行基流分割计算,验证数字滤波法F1 法在皖南地区的适用性。由计算结果可知,东津河、西津河平均误差分别为5.32%、8.00%。计算所得结果与实测值基本接近,误差率平均在10%以内,基流分割结果与实际过程拟合性较好,进一步确认数字滤波法F1 法在郎川河流域的适用性。
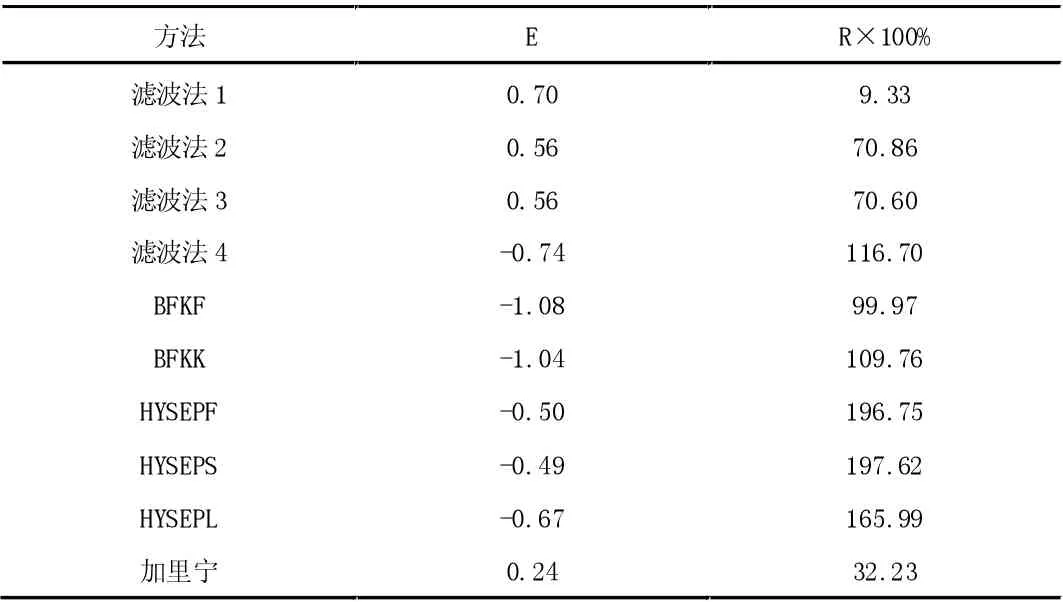
表2 10 种方法验证成果表

表3 东津河、西津河基流分割验证成果表
4 结论
4.1 对基流过程线对比分析,采用Nash-Sutcliffe 方法对10种基流分割方法所得结果进行验证,数字滤波法的FI 法,计算结果与实测值基本一致,效率系数为0.7,相对误差为9.33%,满足效率系数L 超过0.6,平均相对误差R 小于10%,因此由此可知数字滤波法的FI 法较为合理。
4.2 数字滤波法FI 法于该地区适用性更理想,选取东津河与西津河流域进行验证,计算所得结果与实测值基本接近,基流分割结果与实际过程拟合性较好,因此,可知采用数字滤波法在宁国市区域内的东津河、西津河流域进行基流分割较为合理。

