不同基流分割方法在秦岭山区-黄土高原过渡带的对比应用及其演化规律研究

樊晶晶， 刘纯， 穆征， 赵雪花， 林帅， 孙雪， 黎云云

(1.河北工程大学 水利水电学院,河北 邯郸 056038; 2.太原理工大学 水利科学与工程学院,山西 太原 030024;3.绵阳师范学院 资源环境工程学院,四川 绵阳 621000)

河川基流是指地下含水层向地表径流补给的一种慢速流，其所反映的主要是地下水与地表径流间的互馈关系。当流域没有产生降水以及处于干旱期时，基流是维持河流基本水量的主要来源，也是维持河流生态系统健康发展的关键因素。由于干旱半干旱区的降水量少、蒸发量较大且地形多变，河川径流分布也不均匀，这使得占河川径流量比值较大的河川基流成为维系河流运动的关键成分。比如：在黄河唐乃亥站以上流域，多年平均基流量占到了河川径流量的65%[1]；渭河咸阳站多年平均基流量约占河川径流总量的67%[2]。正如很多文献所指出的，河川基流的变化规律反映了河道水量和地下水位的互补演化关系[3]，在维持水源稳定性、持续性以及保证河流生态需水、工业城市供水、农业灌溉等方面起到了关键性的作用[4]，且对河流生态环境保护和水资源开发具有非常重要的意义[5-6]。

基流分割一直是水文学及水资源领域的研究热点和难点[7]，其对流域水文分析与计算、区域水资源调查、评估以及管理等都意义重大[8-9]，且其分割结果对降雨-径流关系分析以及坡面汇流计算的精度有重要影响[10]。众所周知，受基流观测水平和空间差异性的制约，基流尚没有有效的检测手段，也无法通过一定试验方法大范围测得。因此，针对不同的研究区域，专家学者提出了不同的基流分割方法。总结现有分割方法，可按照其分割原理将其划分为5类[11-14]，即图解法、同位素法、水文模拟法、数学物理法和数值模拟法。其中，图解法较为简单，但是人为的主观性很强，效率相对较低，精度无法保障且无法确定误差来源。目前，这种方法是基流分割的基本方法[3]，但不适合长序列基流分割。同位素法的可操作性和可靠性都比较好，但容易引发水体污染[15]。水文模拟法以及其他数学物理法虽然在物理上意义清晰、明确，可信度也比较高，但是需要调节的参数较多，计算复杂，对技术人员的要求也相对较高[16]。随着现代计算机技术的快速发展与普及，数值模拟法在实际工程中得到广泛的应用，可以有效并快速地得到稳定和持续的基流过程，相关方法主要包括数字滤波法、BFI(Base Flow Index)法、HYSEP(Hydrograph Separation Program)法、平滑最小值法等[17]。近年来，基流分割方法不断拓展外延，许多学者在基流分割方面也取得了很多有价值的研究成果。如：杨士娟[18]基于直线斜割方法，配合AutoCAD软件开展了基流分割研究，发现无定河流域的基流在河川径流量中占比较高；雷正国[19]对长河上游径流序列分割后，发现Lyne-Hollick滤波法和Boughton-Chapman滤波法能够很好地实施基流分割，并且分割得出的过程线也比较稳定，能够比较准确地辨识各个水平年之间的基流过程，有效验证了这两种方法在该流域的适用性；董晓华等[20]经过多方法的对比分析发现，在三峡坝址以上流域两参数的数字滤波法比其他分割方法更合适；林学钰等[21]通过直线平割法和BFI法，计算了黄河的基流过程，并基于此制定了黄河流域的水资源管理方案；于艺鹏等[22]梳理了9种基流分割方法，并对分割方法的适宜性进行对比，得出BFI法的分割结果和HYSEP法的分割结果比较相似，但从综合变异性、过程线相吻合的情况和基流是否稳定等多方面的分析认为，修正的BFI法更适用于黄土区的相关研究。此外，为了深入分析基流分割方法在我国锡林河流域的实际应用情况，焦玮等[23]运用数字滤波法、HYSEP法、平滑最小值法和加里宁法，分别实施了基流分割并分析其适用性，结果表明：平滑最小值法和HYSEP法分割得到的基流过程线平滑缓慢，更符合实际情况。综上可知，基流分割方法并不是普适的，不同流域适用的分割方法存在客观差异。

鉴于此，本文拟在秦岭山区-黄土高原过渡带分析不同基流分割方法的适用性，并对不同方法(9种)的计算结果进行对比分析，从而选出秦岭山区-黄土高原过渡带渭河流域较为可靠、稳定且适宜的分割方法，为秦岭山区-黄土高原过渡带的社会经济可持续发展、水资源评价和综合开发利用等提供科学依据。

1 研究区域及资料

渭河是黄河最大的支流，起源于甘肃省渭源县鸟鼠山，主要流经甘肃、宁夏和陕西3省。渭河干流总长818 km，总流域面积约134 766 km2，位于秦岭山区-黄土高原过渡带，是过渡带的典型区。流域属于温带大陆性气候区，多年平均气温6～13 ℃，多年平均降水量572 mm[24]，且降水量年际变化幅度较大，基本呈东南多西北少的态势，6—9月份是主要降水期[25]。流域蒸发较为强烈，平均蒸发量为509.8 mm。流域站点分布如图1所示。

图1 研究区域及站点分布

文中所使用的气象数据来自中国气象科学数据共享服务网(http://data.cma.cn)，涉及渭河流域及周边21个气象站。所采用的华县站径流数据，来自《黄河流域水文年鉴》。气象数据和径流数据系列的历时均为1960—2010年。

2 基流分割方法

2.1 数字滤波法(F1—F5法)

数字滤波技术是重要的信号处理方法[26]，已在国际上被广泛应用，其特点在于可充分利用长历时径流资料来分析和计算基流，且其客观性和可重复性较好[13，27-28]。

方法1(F1法)：Lyne-Hollick滤波法是Lyne和Hollick于1979年首次提出，并由Nathan和Mcmahon于1990年引用到水文中进行基流分割[30]，其分割方程为：

(1)

Qbt=Qt-Qst。

(2)

式中：Qst和Qs(t-1)分别为第t时刻和第t-1时刻的地表径流量；Qt和Qt-1分别为第t时刻和第t-1时刻的径流量；Qbt为第t时刻的基流量；f1为滤波参数，据NATHAN R J等基于0.90～0.95范围内的效果比较，推荐滤波参数f1取0.925[31]。

方法2(F2法)：CHAPMAN T在1991年的研究中对F1进行了改善，并首次提出了Chapman滤波法，其分割方程为[32]：

(3)

Qbt=Qt-Qst。

(4)

式中f1一般取值为0.95[19]，其他参数意义同F1。

方法3(F3法)：CHAPMAN T和MAXWELL假定某时刻的基流量为该时刻的地表径流量和前一时刻基流量的加权平均[33]，其分割方程为：

(5)

式中k为退水参数，一般取0.95[13]。

方法4(F4法)：1999年，CHAPMAN T又提出了Boughton-Chapman滤波法[34]，其分割方程为：

(6)

式中：k为退水系数，一般取值为0.95；f2为固定参数，一般取0.15[26]。

方法5(F5法)：ECKHARDT K在2005年提出了Eckhardt滤波法，其可通过BFImax取值来调整基流过程，其分割方程为[35]：

(7)

式中：BFImax为最大基流指数；α为退水常数[6]。

经研究，ECKHARDT K给出了BFImax的取值建议，即多孔含水层的多年性河流取0.8、季节性河流取0.5、坚硬岩石含水层的多年性河流取0.25。而退水常数α一般可取0.95～0.98[36]。由于渭河流域降水量少，且降水是地下水的主要补给源，受到季节性影响比较明显[37]，故该研究区BFImax取0.5，α取0.98。

2.2 平滑最小值法(F6法)

平滑最小值法是英国水文研究所在1980年首次提出的一种基流分割技术[2]，其原理主要是将年内日流量序列以5 d为一个独立的单元进行划分，使其形成互不重叠或相容的块，并对每个独立的单位块中的最小值进行筛选，即在给定条件下，将满足条件的最小值提取出来，再用一条直线与每个拐点相连，从而得到一个基流序列。具体计算步骤为：

步骤1 块的区域划分。将流量序列Qt(t=1、2、…、n)以5 d为一个单元划分成m个互不重叠的块[20]。如果一年的天数n不是5的整倍数，则将最后一个不完全的块除去。实践证明在多数流域中，以5 d为一单元进行日流量序列计算都是比较准确的。

步骤2 选出最小值。筛选每个块中的最小值，命名为q1、q2、…、qm。

步骤3 明确拐点。考虑到地下径流的稳定性，经过大量科学研究和理论实践[2]，拟采用如下拐点经验计算公式：划分最小值序列，如(q1,q2,q3)，(q2,q3,q4)、…、(qm-1,qm,qm+1)，并从中挑选出满足条件kqm≤min (qm-1,qm+1)数据集(k取0.9)，并将qm确定为基流过程线上的一个拐点。

步骤4 计算基流。重复第3步，求出所有拐点，并用线性插值法求出相邻拐点的基流值，从而得到基流过程和基流总量。

2.3 局部最小值法(F7法)

时间步长法[38]是由PETTYJONH W A和HENNING R于1979年首次提出的。该方法可分为3种，即固定步长法、滑动步长法和局部最小值法。其中，局部最小值法主要是通过比较水文曲线的斜率，简单地将局部最小点连接起来。本文拟选用LIM Kyoung Jae等2004年开发的基于网络水文分析工具WHAT(https://engineering.purdue.edu/～what/)中的局部最小值法开展基流分离[39]。

2.4 基流指数法(F8、F9法)

基流指数(Base Flow Index)法，是英国水文研究所(Institute of Hydrology)在1980年首先提出的一种基流分割方法[40]，简称BFI法。其工作原理主要是将一年内的日流量数据划分为365/N个时段，然后选出每段最小值乘以拐点检验因子，当乘积小于相邻时间段的流量最小值时，则认为它是一个拐点。重复此次检验操作，直至选出所有的拐点，然后用直线将所有拐点连接，连接成一条流量过程线，其下方的面积为基流量。目前，BFI法分为两种：一为标准BFI(f)法，这里简称F8法；二为改进的BFI(k)法，这里简称F9法。拐点因子的不同是两种方法的唯一区别，根据经验一般取值f=0.9和k=0.979 15[41]。基流指数法在进行长时间序列的基流量计算和大量数据的处理上有较大优势，尤其是在多年数据分析中具有较高的可信度[17]。

3 贡献率分析方法

双累积曲线法是目前用于水文气象要素一致性检验与长期演变趋势分析的最简单、直观和广泛的方法之一[42]。文中拟采用该方法进行变异点分析，划分基准期和影响期，并基于时段划分结果分离评价气候变化和人类活动对径流和基流变化的贡献率。具体计算方法如下[43]：

1)对变异前的累积降水量∑P，累积径流量或累积基流量∑R进行回归分析，得到关系式：

∑R=k∑P+b。

(8)

2)基于上述线性回归方程，根据影响期累积降水量∑P计算累积径流量或累积基流量，得到∑R。由于该结果为线性方程外推获得，故∑R的下垫面和人类扰动条件与基准期的相同，其值表征了影响期无人类活动扰动下的径流或基流累积量。

3)用计算出的∑R反推年径流量或年基流量，然后求得两阶段实测和计算年径流量或年基流量(1-基准期，2-影响期)的差值δ，由此可求出气候变化和人类活动影响对径流和基流的影响量。

δ人=R2实测-R2计算，

(9)

δ气=R2计算-R1实测。

(10)

式中δ人和δ气分别表示由于人类活动和气候变化影响而引发的径流或基流的变化量，mm。

4)人类活动和气候变化对径流和基流变化的贡献率公式为：

(11)

式中：Q为人类活动和气候变化对径流量或基流量变化的贡献率；E为基准期和影响期实测径流量或基流量的差值，mm。

4 结果分析

采用9种方法分别对秦岭山区-黄土高原过渡带渭河干流华县站1960—2010年日流量数据实施基流分割。

其中，在基流指数法(F8和F9法)中，为了确定N值，需要首先分析N值与基流指数的关系。为此，本文通过水文频率分析法选取了序列代表年：丰水年(1988年)、平水年(1969年)和枯水年(2008年)。然后建立了基流指数与N值的关系，如图2和图3所示。图中，以N天为一个时段，从1取到10，N≥4时，各水平年的基流指数趋于稳定。即以N=4为一时段来进行基流分割。

图2 F8法基流指数与N值关系图

图3 F9法基流指数与N值关系图

4.1 各方法基流量的特征分析

通过9种分割方法获得基流序列，将基流序列的均值、Cs、Cv、趋势性、持续性、最小值、最大值以及极值比进行统计分析，结果见表1。由表1可知：从均值来看，均值存在差异，F1、F4、F5、F7的较大，其余法的均较小；从偏态系数Cs来看，Cs值均大于0，呈右偏分布，说明基流量大多集中在小于均值的部分；从变差系数Cv值来看，各方法获得的基流系列离散程度一致，Cv值均处于0.526～0.589；从趋势性来看，在置信度为95%(Uα/2=1.96)，检验统计值U值均为负值，在置信区间外，均呈显著减少趋势；从持续性来看，Hurst指数值均大于0.6，存在显著的正持续性；从极值比来看，数字滤波法和F7法计算的基流量极值比较小，其中F4法的计算结果最小。

表1 不同方法分割基流量特征值

4.2 各方法基流指数分析

基流指数为某时段内河川基流量与径流总量的比值，反映河川基流量的大小[3]。9种分割方法在丰水年、平水年和枯水年计算得到的基流指数如图4—6所示。

图4 丰水年基流指数图

图5 平水年基流指数图

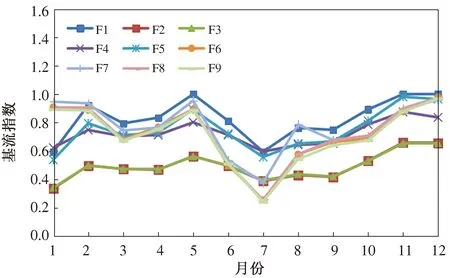
图6 枯水年基流指数图

图4—6显示，不同年型的基流指数均呈现先减小后增大的趋势。其中，丰水年(图4)中各方法计算的基流指数的稳定性最好。受汛期的影响，平水年(图5)中各方法计算的基流指数变化程度均较大，而在枯水年(图6)仅F6—F9法计算的基流指数波动较大，其余方法计算的则较为稳定。

在不同时间段内，各基流分割方法计算的基流指数见表2。由表2可知：各方法计算的基流指数差异较为明显，其中，F1、F4和F7法的计算结果较大，分别为0.664、0.673和0.680；F2、F3、F5、F6、F8和F9这6种方法计算的基流指数较为接近，基本处于0.411～0.541范围内，计算值小。

各方法分割结果基流指数的最大值、最小值、极值比和标准差见表3。由表3可知：从标准差来看，数字滤波法的小于其他3类方法，特别是F2与F3法的标准差最为显著；从极值比来看，数字滤波法(除F5外)与其他方法的极值比相比也更小，而平滑最小值法(F6法)与BFI法的极值则相对比较大，由此可见数字滤波法在所有方法中较为稳定。从以上分析发现，F2和F3法计算的基流指数比较接近，标准差与极值比均较小，计算出的基流稳定性较好。

表2 不同分割方法计算的基流指数

表3 不同分割方法计算的基流指数统计值

4.3 典型特征年基流过程分析

本文选取丰水年为代表年，9种方法的基流分割结果如图7所示。由图7可知，9种基流分割方法获得的基流过程线和径流过程线的趋势均具有较好的一致性。

数字滤波法中，F1法(图7(a))、F4法(图7(d))的基流分割过程非常接近，过程线具有峰值高且尖锐、起伏程度较陡的特点。F2法(图7(b))与F3法(图7(c))的过程线起伏程度小，曲线平滑且分割结果相近，基流过程与其他方法的相比，较符合一般的基流过程，且平稳性较好。F8法(图7(h))、F9法(图7(i))和F5法(图7(e))的基流过程相似，起伏程度较小。但在汛期内，基流随地下水变化而逐渐消退的现象并未显著体现出来。由F6法(图7(f))的基流分割过程可发现，因为对径流序列采用了线性内插的处理方式，导致分割的过程线多由折线段组成，拐点多、平滑度低。局部最小值法(图7(g))(F7法)分割的基流量相对较大，基流过程线随径流过程上升和下降迅速，基流过程线和径流过程线的变化趋势一致性较高，变化过程不真实，这就直接说明了分割结果不能充分符合汇流时的阻尼和迟滞效应。不同的方法适应不同的区域，从前人的研究成果来看，数字滤波法的分割结果较为稳定，并已得到广泛应用，在不同地区还是具有良好的适应性的[44-47]。

综上所述，笔者认为在采用的9种基流分割方法中，数字滤波法中F2法(图7(b))和F3法(图7(c))计算的基流量在年内和年际尺度上的稳定性最好，对秦岭山区-黄土高原过渡带而言，是比较可靠的基流分割方法。

图7 9种基流分割方法结果对比

4.4 不确定性分析

为验证基流分割的可靠性，以F3法为例，采用蒙特卡罗法[48]进行不确定性分析。

假设退水系数k服从正态分布，均值取0.925，标准差分别为0.008和0.025，分别随机生成50个符合样本特征的退水系数，如图8所示。

图8 退水系数k的概率密度图

根据随机生成的样本进行基流计算和可靠度分析，结果如图9所示。其中，两个正态分布生成随机数时，采用了同样的均值，因此其在50%可靠度上对应的基流量相等。文中以参数k=0.95计算的基流量的交点代表其可靠程度，结果显示可靠度均在80%以上，遂可证明F3法分割的基流具有较高的可靠度。

图9 基流量的可靠度

5 演化特征

基流在秦岭山区-黄土高原过渡带社会经济与生态环境的发展中起着重要作用。认识并分析渭河的河川径流、基流的历史演化过程及其发展规律，对深入地了解秦岭山区-黄土高原过渡带水资源的形成演化，进而合理开发和利用区域水资源具有重大意义。本文基于数字滤波F3法的计算结果，分析了基流量、径流量以及基流指数的年内变化(多年平均)以及1960—2010年的演化过程与基流的演变特征。

5.1 年内变化特征

图10显示了研究区内华县站径流量、基流量与基流指数的年内变化情况。由图可知：华县站年径流量主要集中于汛期6—9月，9月年径流量最大；由于4—5月和10—11月处在汛枯交替期[25]，出现径流量突增或突降的情况；基流指数呈现先减小后增加的趋势；其中，7月的基流指数最小，8—9月的基流指数相较其略有增加；8月主要是由于延时补给地下水驱动下一时段基流增加，且基流量增幅大于径流量增幅所致[49]，而9月则主要归因于径流量的大幅衰减；12月进入枯水期，降水偏少，相应的河川径流量明显减少，基流成为河道径流的主要来源，基流指数也相应增大。

图10 径流量、基流量与基流指数的年内变化

5.2 年际变化特征

对渭河华县站年径流与基流序列进行线性回归和箱线图的分析，梳理了年径流与基流的变化趋势，其结果如图11和图12所示。由图11可知，在1960—2010年间，基流量的涨落规律与年径流量基本一致，约占年径流总量的48%。统计结果表明，年径流量与基流量的线性回归增长率分别为-1.129和-0.545，基流指数较为平稳，地表径流与地下水的交换关系相对稳定。箱线图(图12)中，径流量较基流量波动较大，具有明显的代际差异。其中：基流量和径流量均在20世纪60年代质心最高，离散程度最大；在20世纪90年代和21世纪00年代，基流量和径流量质心最低，离散程度最小。总体来看，20世纪60年代至21世纪00年代，径流量与基流量具有显著下降趋势，离散程度逐渐降低。

图11 径流量、基流量与基流指数的年际变化

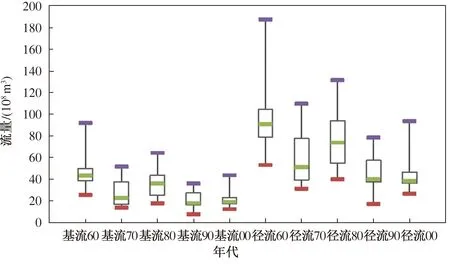
图12 径流量与基流量的代际变化

6 秦岭山区-黄土高原过渡带基流变化驱动力分析

采用双累积曲线法对径流和基流变化进行驱动力分析，主要基于数字滤波法之F3法的基流分割结果，对20世纪60年代至21世纪初的径流、基流、降水、气温和蒸发量进行统计分析，确定基准期和影响期，并开展气候变化和人类活动的贡献率分析。

径流、基流、降水、气温和蒸发量的代际变化情况见表4。由表4可知：各代际中，降水、径流和基流的峰值均出现在20世纪60年代，其整体呈现先增大后减小再增大的变化趋势；与其不同，气温和蒸发量整体呈现先减小后增大的趋势，最低值出现在20世纪80年代，较60年代分别减少了0.66 ℃和40.88 mm。鉴于各因素均在20世纪70年代及以后发生较大变化，因此可设定20世纪60年代以前为基准期，70年代及其以后为影响期，来实施径流和基流变化的驱动力分析。

首先，以1960—1969年为基准期，建立降水-径流和降水-基流双累积曲线，如图13、图14所示，图中“↓”为基准期与影响期分界点。依据公式(8)—(11)进行计算分析，得到径流与基流的变化量及影响归因，结果见表5。由表5可知：基准期实测多年平均径流深为90.30 mm，多年平均基流深为43.51 mm；而影响期内，人类活动及气候变化对径流的影响量可达到36.86 mm，其中由气候变化驱动的径流减少量为3.4 mm，人类活动对径流衰减的贡献量为33.46 mm，所以人类活动是导致径流显著减少的主因，其贡献率高达90.78%；而人类活动和气候变化对基流的影响总量为18.57 mm，其中气候变化驱动的减少量为1.56 mm，人类活动驱动的减少量为17.01 mm。同样，人类活动也是导致基流衰减的主要因素，其贡献率达91.60%。

该结果与郭爱军等[50]研究的渭河人类活动和气候变化对径流影响的定量分析结果类似，都认为气候变化对秦岭山区-黄土高原过渡带的径流变化有重要影响，但人类活动起着决定性作用。

表4 降水、气温、蒸发、径流、基流的代际变化表

图13 降水与径流深双累积曲线

图14 降水与基流深双累积曲线

表5 气候变化和人类活动对径流和基流变化的贡献率

7 结语

1)应用9种基流分割方法计算得到的秦岭山区-黄土高原过渡带的基流指数受汛期降雨影响，其年内分布均呈现先减小后增大的趋势，且平水年和枯水年基流指数波动较大。

2)研究区的代际基流指数位于0.374～0.734范围内，但不同基流分割方法计算得到的基流指数值差异比较大。从多年平均值看，F2、F3、F6、F8和F9这5种方法计算得到的基流指数值偏小，但相对接近。从标准差和极值比来看，F2和F3法算得的相对偏小，表明结果较稳定，认为在秦岭山区-黄土高原过渡带，采用数字滤波法进行基流分割更优。

3)基流过程分析结果表明，F2与F3法计算出的基流过程起伏程度小，曲线平滑且分割结果相近，基流过程较平稳，较为符合基流过程线的一般情况，且可靠度高，可作为秦岭山区-黄土高原过渡带的一种较为可靠的基流分割方法。

4)基流是秦岭山区-黄土高原过渡带枯水期径流的主要来源，约占河川径流总量的48%。

5)秦岭山区-黄土高原过渡带径流量和基流量下降趋势显著，但基流指数平稳，无明显趋势，表明河水与地下水的交换关系相对稳定。

6)秦岭山区-黄土高原过渡带基流变化驱动力分析结果显示，人类活动对基流变化起着决定性作用。