基于自适应引导滤波的水利工程逆向模型降噪方法研究

刘尚蔚, 杨阳, 赵继伟

(华北水利水电大学,河南 郑州 450046)

随着倾斜摄影技术的不断发展,无人机摄影测量技术在水利工程中得到了广泛应用[1]。无人机摄影测量具有低成本、高效率的特点,弥补了传统近景摄影测量布控困难的问题,在逆向建模过程中具有独特的优势。面对水利工程体积庞大、基岩表面不平整的特点,无人机倾斜摄影很好地解决了效率的问题,但由于倾斜角度的限制,造成了部分地面视角数据的丢失。对此,文献[2]研究了LiDAR点云辅助的航空影像空中三角测量,提高了航空影像数据的定位精度；文献[3]在倾斜摄影的基础上加入了双手机成像摄影系统,实现了空地一体的三维重建；文献[4]利用无人机和激光扫描仪对建筑物进行了联合三维建模。这些倾斜摄影与近景摄影结合的逆向建模三维重建方法,克服了单一数据源的局限,进一步完善了逆向建模的数据来源。

然而,无人机在采集图像的过程中,易受到外界环境因素和图像采集设备本身的影响,尤其是水利工程通常所处测量环境差,导致图像几何信息略微偏差,对三维重建产生了较大的影响。文献[5]基于经验小波变换算法思想对无人机采集的图像进行了直接降噪,实现了较好的图像降噪效果,但该方法仅停留在平面,未就三维重建后的模型进行处理分析。文献[6]根据点云滤波非地面数据获取建筑物高度等信息,结合无人机采样纹理进行三维重建,实现参数化建模,但这种方法严重依赖人工干预,工作量巨大,无法满足水利工程快速建模的需求。文献[7]采用二次滤波的方法减轻了三维匹配块在平滑区产生的抓痕现象,但该方法无法处理边缘噪点产生的锯齿状纹理。文献[8-10]对边缘检测算子进行了讨论,分别提出了边缘保持的方法,但面向信息量较大的水利工程模型时效率很低,不适合推广。

针对以上问题,本文以引导滤波算法[11]为基本思想,从近景摄影和无人机倾斜摄影三维重建的模型出发,对该模型进行简化等预处理,提出了一种适用于水利工程依据边缘信息进行引导滤波的自适应算法,以提高逆向建模的精度。

1 水利工程逆向建模技术

对于水利工程,本文采用倾斜摄影测量和近景摄影测量结合的方法获取原始模型信息,对倾斜摄影测量进行运动结构恢复,并辅以地面近景摄影测量进行矫正,实现对实体水利工程的逆向建模。

本文利用无人机对水利工程进行倾斜摄影测量,获取测区目标物几何信息,同时记录无人机定位信息和相机焦距等属性；使用广义成像仪实现地面上的近景摄影测量,在地面视角实现无人机无法获取的凹陷部信息获取,完善无人机倾斜摄影的不足。将获取的倾斜摄影和近景摄影数据导入ContextCapture软件,通过空中三角测量计算获取空中影像外方位元素,结合地面近景摄影信息构件不规则三角网(Triangulated Irregular Network,TIN)模型,最后在空间中进行纹理映射生成三维重建模型,以obj格式文件导出。上述三维重建的技术流程如图1所示,以某拱坝枢纽为测区所建立的逆向模型如图2所示。

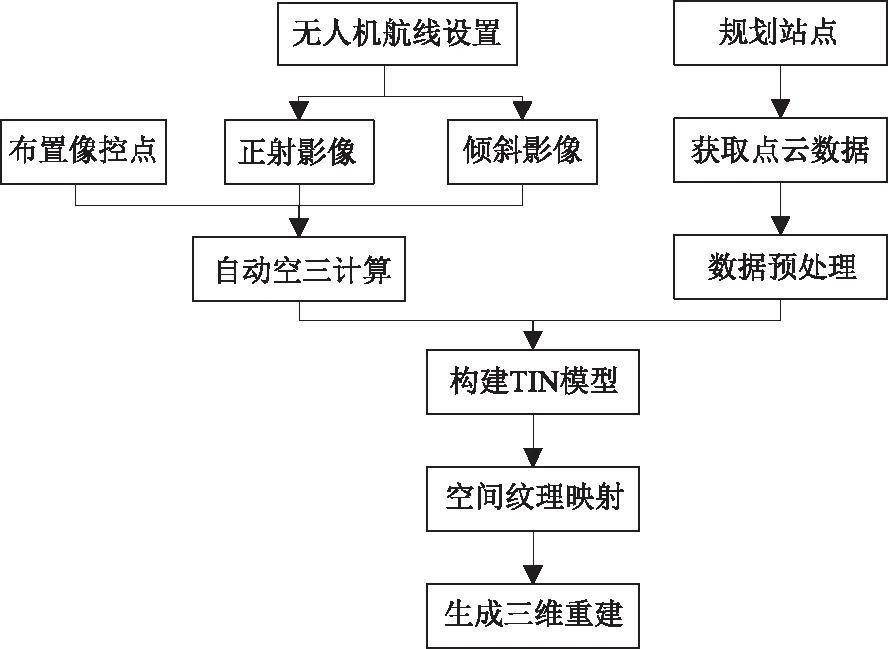
图1 倾斜摄影协同近景摄影三维重建技术路线

图2 倾斜摄影协同近景摄影逆向建模生成的某拱坝枢纽模型

由采集误差导致部分未经上述过程成功配准的像素点在模型中生成了噪点,形成了三维重建后的误差。无人机采集信息过程中的误差来源于采集设备和外界环境的变化,该误差服从均值为0的正态分布[12]。由此,为进一步提高三维重建的精度,本文采用滤波的原理对上述过程生成的三维重建模型进行进一步处理。

2 引导滤波及相关原理

2.1 曲率下采样

曲率下采样,即在点云曲率越大的地方采样点越多。取某点为中心的邻域进行研究,计算点与邻域法线的夹角值,夹角值越大说明曲率越大。设定一角度阈值,若某点邻域夹角值大于该阈值,则认为该点处为特征明显的区域；反之,则为特征不明显区域。对特征明显区域和特征不明显区域进行独立的均匀采样,采样数分别为S(1-U)与SU,其中S为目标采样数,U为采样均匀性系数。

点T邻域窗口大小的控制决定了局部纹理的性质,其中包含的采样点个数t为重要参数。对此,本文在点K处设一半径为R的球面,球面以内的点为所求邻域点,该球半径R为自适应取值。

这种采样由于在水工逆向模型中特征明显区域的采样密度大,故计算效率高。通过几何特征区域的划分,使得采样结果具有强的抗噪性、高的稳定性。

2.2 离群统计消除

假设模型服从高斯分布,其结构由均值和标准差决定,平均距离在指定范围(视为全局平均距离和方差的函数)之外的点可视为离群点剔除。为提高检索速度,可应用KD树对点云进行索引[13]。

某点到所有K邻域点的平均距离Da按式(1)计算：

(1)

式中：K为邻域中所有点的数量；i为邻域中点的索引值；Di为该点到邻域中第i个点的空间距离。

统计分析所有点平均距离Da的平均值D以及方差S2,分别按下式计算：

(2)

(3)

式中：n为模型中点的数量；j为模型中点的索引值。

离群点判定阈值DT定义为：

DT=D+αS2。

(4)

式中α为松弛系数,按照试验与训练的需求进行设定。

若某点的Da>DT,则剔除该点；反之,则保留该点。

2.3 引导滤波原理

引导滤波是一种局部线性滤波器,对图像平滑滤波的同时还保持了边缘细节,通常用于二维平面图像,稍加修改可用于图2中三维重建的水工模型。首先定义一个通用的线性平移变量滤波的过程,包括一个引导图像I、一个滤波输入图像p和一个输出图像q。引导滤波的关键是引导图像I与输出图像q之间的局部线性模型,假设q在I中以点k为中心的区间wk进行线性变换：

qi=Akpi+Bk,∀i∈ωk。

(5)

式中：i、k为点的索引值；ωk为中心位于k时的窗口,半径为Ra,Ra为输入参数；qi为滤波后输出的三维点；pi为输入三维点(假设与引导图像存在对应关系，替代引导图像对应点)；Ak为一个3×3的方阵；Bk为一个3×1的矩阵。

从滤波器的约束中输入p,在模型输出q的过程中,除去输入p中不需要的成分n(如噪声和多余的纹理)：

qi=pi-ni。

(6)

上述基本原理如图3所示。

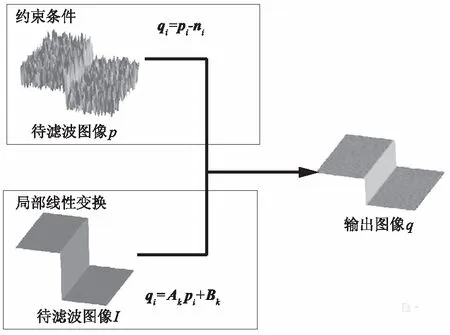
图3 引导滤波原理

引导滤波模型中回归模型是假设的解析表达式,此时图像为二维函数,可用系数ak和bk分别替换式(5)中的Ak和Bk。对于该回归模型,要求有合理的系数ak和bk使输入值p与输出值q之间的差距最小,转为最优化问题,即：

(7)

式中：e为向量(1,1,1)；ε为ak的规整因子,为调节引导滤波效果的重要参数,用于防止所求的ak过大。

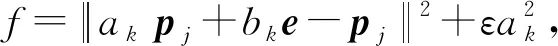
(8)

(9)

(10)

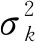
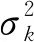
2.4 Marr-Hildreth算子改进的引导滤波

原生的引导滤波,在不同的窗口采用了相同的规整因子ε,显然是未考虑到不同窗口中点云的纹理存在的差异。根据2.3节的结论,对于纹理多变、边缘梯度信息丰富的窗口,线性模型系数ak的值偏大,需要较小的规整因子ε来修正；而对于边缘梯度平缓的窗口,需要调整更小的规整因子ε来减小逼近误差。因此,有必要根据不同的窗口对规整因子ε进行自适应调节。LI Z等[14]对引导滤波进行了改进,该方法将以窗口内的方差定义加权因子,对规整因子ε进行自适应调整。实际上,方差定义的加权因子并不能很好地反映图形的边缘信息。

本文将加权引导滤波的思路引入至水工模型的修正中,同时考虑到水利工程模型信息量大的特点,利用Marr-Hildreth算子重新定义加权因子。这种算子将高斯滤波和拉普拉斯算子结合[15],可以给出封闭的边缘边界,并且能够避开递归滞后的计算过程,从而减少了堆栈要求。定义边缘权重Marr-Hildreth算子如下：

(11)

式中：Mi为当前窗口的Marr-Hildreth边缘检测算子;Mi′为引导图像的Marr-Hildreth边缘检测算子;N为引导图像中像素点数量;i′为对应索引值;i为当前窗口中点的索引值;η为固定值。

由于Marr-Hildreth算子为二阶Laplacian算子的一种,在边缘处具有较大的幅值,因此在边缘处点的ri>1,在平滑处点的ri<1。经过试验与训练发现,自适应于Mi值变化的η有利于提高算法的鲁棒性,对此,本文中η取为|Mi|最大值的0.1倍,效果较好。

将式(11)称为Marr-Hildreth加权引导滤波算子,替换2.3节中的ε为ε/ri,式(7)替换为本文求解引导滤波线性参数方案,即：

(12)

3 基于引导滤波的水工逆向模型降噪方法及实现

3.1 基于引导滤波的逆向建模降噪方法

对于初步建立的三维模型,为减少后续工作的计算量,并尽可能保留局部线性变化效果,对该模型进行曲率下采样工作。由于离散的点云之间不存在拓扑结构,为了得到其几何属性,通过各点的邻域结构来识别点云的几何特征,进行低尺度离群点的剔除,得到引导模型。基于引导滤波原理利用引导模型对原模型进行平滑处理,引入边缘检测算子实现该原理对模型细节纹理的自适应调整。具体降噪方法步骤如下：

1)对于水工逆向建模obj格式的三维模型,使用pcl_mesh_sampling程序进行整体点云采样,获得模型原始点云数据。由于水利工程模型曲率变化不均匀不连续,这种整体采样的均匀采样方法会在曲率较小处获取同样密度的点,造成后续工作需求计算量变大。为减少这种曲率不同产生的计算量浪费,本文对点云原始模型依据曲率大小按照2.1节中的原理进行二次采样,以降低后续工作计算量。

2)为消除设备收集数据时产生的部分噪声和伪影造成过大的点云偏差,引入低尺度统计离群消除滤波算法,按照2.2节中的原理,依据各点到其邻域内所有点的平均距离,将超出阈值距离过大的离群点剔除。按照该方法对曲率下采样后的模型进行离群点的剔除,减小水工逆向模型中偏差过大的离群噪点,获得引导滤波中所需要的引导模型。

3)利用统计离群点处理后的引导模型对采样后的待滤波模型进行引导,依据2.3节中原理,按照式(1)的方法进行引导滤波。在求解引导滤波的过程中,依据2.4节中改进原理,以式(12)为依据求线性变换参数ak与bk,通过局部线性变换与约束条件完成对待滤波水工模型的平滑处理。

上述方法技术路线如图4所示。

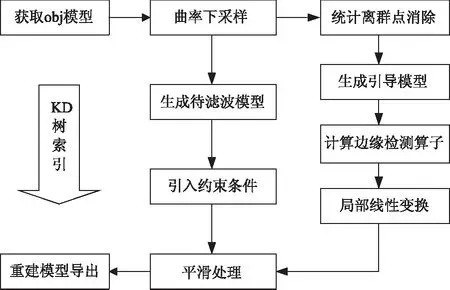
图4 本文处理方法技术路线

3.2 运用Python语言的程序设计

Python提供了高效的数据结构,可以简单地面向对象编程,能够在多数平台上运行,同时方便扩展新功能,本文调用了Numpy和Open3D扩展程序库。Numpy代表了“Numeric Python”,是由多维数组对象及用于处理数组的例程集合组成的程序库,相对于Python list不需要做类型检查,可减少代码的冗余,提高程序运行速度。Open3D是用于处理三维数据的程序库,支持快速开发和处理3D数据,可对点云进行操作及可视化。本文基于引导滤波的水利工程逆向模型降噪方法的部分步骤中关键Python程序如下：

1)将ply格式的点云文件与程序放入同一目录中，具体程序代码如下：

import numpy as np

import open3d as o3d

pcd = o3d.io.read_point_cloud(′ex.ply′)

2)根据曲率判定点的特征是否明显,分别对特征明显点和特征不明显点进行均匀采样,拼接点云,主要程序代码如图5所示。

图5 曲率下采样主要程序代码

3)通过KD树索引计算点云密度,主要程序代码如图6所示。

图6 计算点云密度主要程序代码

4)通过定义的阈值剔除离群的点云。主要代码如下:

c1,ind = pcd.remove_radius_outlier(K,D)

radius_cloud = pcd.select_by_index(ind)

5)定义引导滤波函数,在每个窗口内求解线性变换参数,对点进行线性变换,循环处理每个窗口,并输出点云,部分程序代码如图7所示。

图7 部分引导滤波函数代码

4 试验与分析

4.1 试验方法

为验证本文方法的有效性,利用Python语言对上文的方法编程实现。试验使用的计算机硬件配置为AMD Ryzen 7 4800H的CPU,32G内存,使用NVIDIA GeForce RTX 2060的GPU进行加速,操作系统Win10 64位,运行环境Python 3.7。将obj模型和pcl_mesh_sampling.exe文件放入同一文件夹下,在cmd中打开该文件夹目录,运行pcl_mesh_sampling.exe程序,输入obj模型并输出pcd格式点云文件,在MATLAB中利用pcwrite命令将pcd格式转换为ply格式的点云文件,如图8(a)所示。按照3.1节中的方法,将py文件与ply点云文件放入同一目录下运行Python程序：

1)按照曲率大小对点云采样,效果如图8(b)所示,模型坐标点由36 004个降至28 533个；

2)对采样后的点云模型统计离群点并剔除,效果如图8(c)所示；

3)利用剔除离群点后的模型对曲率下采样后的模型做引导滤波,效果如图8(d)所示。

图8 点云文件降噪过程示意图

本文使用无人机与广义成像仪对某拱坝枢纽进行采样,采用ContextCapture软件逆向建立该工程的obj格式三维模型(如图2),按照上述方法及操作对该逆向模型进行处理,试验中涉及的参数见表1。

表1 试验参数设定

将处理后的模型与原始的模型纹理部分边缘细节进行对比,观察模型噪点变化以及纹理效果,并按《三维地理信息模型数据产品规范》[16]中的规定核实精度要求,与本文方法处理前的模型进行对比,验证本文方法的有效性。在该水利工程中选取30个检查点进行实际坐标测量,作为精度检测的依据。

4.2 试验结果

水利工程三维重建模型中的地形和水工建筑物表面几何结构、曝光度和纹理清晰程度需要达到较高水平。为此,将本文所提出的降噪方法处理前后的三维重建模型进行对比分析。考虑到实验中水利枢纽工程结构较大,为保证对比效果,本文选取4个代表部位结构进行对比,结果见表2。

表2 本文方法对某拱坝逆向模型处理前后纹理对比

由表2中试验结果对比图可以看出：由于运动结构恢复过程中形成了一些离群点和噪点,导致原始建立的模型边缘出现一些锯齿状纹理,甚至部分曲率较小的曲面上出现了不光滑平整的现象。通过本文所述方法处理后,大尺度的离群噪点被统计离群点的方法剔除,小尺度的噪点在本文的自适应引导滤波的算法下得以修正,曲面处理得更加平顺,有效改善了边缘锯齿的现象,在主观上达成了更优秀的视觉体验。

在客观评价上,引入结构相似度指数(Structure Similarity Index Measure,SSIM)与均方误差(Mean Squared Error,MSE)进行定量评价[17]。SSIM反映了两个模型的相似程度,取值在0到1之间,数值越大表示模型三维重建越完整,质量越好。MSE反映了处理前后的模型变化大小,该值越小说明方法效果愈显著。本文将处理前后的三维模型进行比对,得到的SSIM参数为0.86,即处理后的模型较为完整地保留了原始模型的信息；得到的MSE参数为0.15,说明降噪效果比较明显。

根据《三维地理信息模型数据产品规范》中三维模型精度规定的Ⅰ级要求,平面精度中误差(σXY)不高于0.3 m,按式(13)计算；高度精度中误差(σZ)不高于0.5 m,按式(14)计算。

(13)

(14)

式中：X实、Y实、Z实为点的实际坐标,由实测获取；X模、Y模、Z模为对应的点在模型中的坐标；n为检查点的数量,本试验中为30。

由式(13)和式(14)计算可得,未经处理的三维模型在水平精度上的中误差为0.037 m,高度精度中误差为0.031 m；经本文方法处理后的三维模型在水平精度上的中误差为0.032 m,高度精度中误差为0.028 m,水平精度中误差降低了13.5%,高度精度中误差降低了9.7%,合计精度中误差降低了11.9%。上述结果均满足规范中的要求,但显然本文方法处理后的模型更加精准,处理前后两模型各检查点三维误差向量统计如图9所示,并以平均大小为半径做球面作为参考,经本文方法处理后的误差均值由0.046 m降低至0.041 m,降低了11.3%。各检查点累计误差归一化后的方向向量分别为(0.224,-0.588,-0.187)和(0.217,-0.604,-0.189),两向量夹角弧度为0.018 5,基本保持一致,即经本文处理后的模型既降低了原有模型的误差，也保留了原有误差的方向属性。

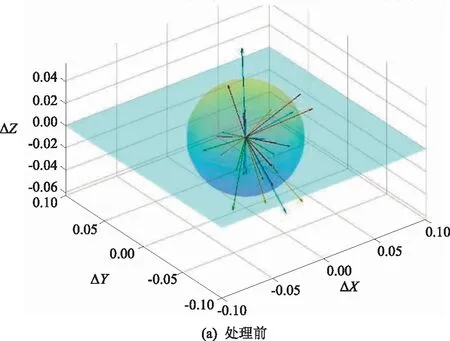
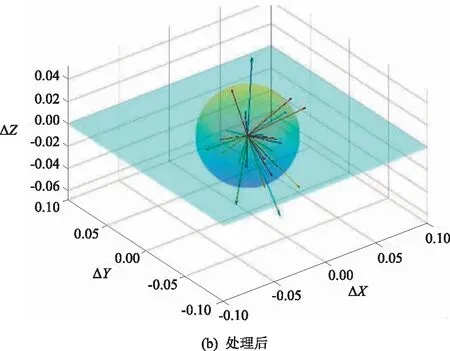
图9 本文方法处理模型前后误差统计

5 结语

本文在多源采集数据建立的模型基础上,采用曲率下采样减小不必要的工作量,并以低尺度的统计离群点剔除获取引导图像,引入Marr-Hildreth算子采用引导滤波对模型进行处理。试验结果表明,本文提出的方法在满足国家相关规范的基础上进一步提高了三维重建的精度(平均误差降低11.3%),模型细节更平顺,改善了边缘锯齿情况,基本保留了采集数据的完整性,同时满足了水利工程快速逆向建模的需求。更高精度的三维重建,可为水利工程施工期信息提供载体,为施工可视化仿真提供更多可能。另外,受当前计算机计算能力的限制,难以快速做到设计模型对摄影采集模型的自动引导匹配。未来，随着计算机计算能力的提高,匹配分块相关算法还需进一步研究,水利工程的逆向建模精度还有提升空间。