让数学核心素养在课堂落地生根

郭利锋

一、现状分析

练习课是一种重要的教学形式。教师经常抱怨，学生学习效率低下，导致教学存在困难。笔者反思发现：首先，教师缺乏对练习课的思考和设计;其次，教师缺乏新的教学思想;最后，教师缺乏解题策略的渗透与指导。笔者认为，教师要先以《新课程标准》理念统领教学思想，重视练习课设计，设计的习题要有深度、宽度;其次，练习课不仅要巩固基本知识，帮助学生形成技能，还要让学生掌握解题方法与策略，促进学生可持续发展。下面，笔者以六年级数学思维拓展练习为例。

二、教学目标

第一，在旧知的基础上拓展延伸，经历“再发现、再建模”的探究过程，发展学生的数学思维。

第二，让学生逐步掌握解题方法与策略，达到举一反三的能力，促进学生可持续发展。

第三，激发学生不断探究知识的兴趣，培养学生善于思考、勇于挑战的思维品质。

三、教学实践

在本节课中，笔者设计了闯三关活动，即三个题组。

第一关：从A点到B点，有两条路，你认为哪条路更近？为什么？（出示图一）

教师问：“为了便于计算，你能用‘几π的形式表示路的长度吗？”

学生答：“两条路一样长，因为这两条路的长度都等于10π。”

教师出示图二，问：“现在两条路还一样长吗？为什么？”

学生答：“两条路还是一样长，都等于10π。”

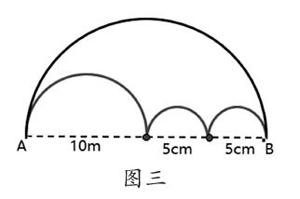
教师出示图三后，学生异口同声地说：“两条路一样长。”教师组织学生思考并讨论：“观察三个图，有什么发现？”

学生1回答：“这些路都等于10π，都一样长。”

学生2回答：“大圆周长的一半等于几个小圆周长的一半。”

学生3回答：“我同意第二个同学的看法，但要在大圆直径等于几个小圆直径和的情况下才行。”

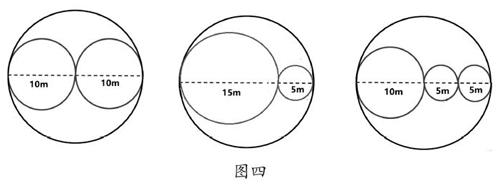
教师追问：“如果把半圆变成整圆，这个规律还存在吗？为什么？”（出示图四）

学生1答：“规律依然存在，大圆的直径是20m，周长就是20π，每个大圆中的小圆直径的和也是20m，所以周长和也是20π。”

教师板书：当大圆的直径等于小圆直径的和时，大圆的周长等于每个小圆周长的和。

教师问：“大圆的直径铺满2个小圆、3个小圆，大圆的周长都与小圆周长和相等，大圆的直径上还能铺满几个圆，是不是也有这样的规律？”

教师引导学生展开想象，并推理得出4个、5个、6个……无数个。

教师出示练习：桌面上画了一条80厘米的线段，还有直径为1厘米、2厘米、3厘米、4厘米、5厘米、8厘米的圆形纸片若干，现在用圆形纸片将桌上线段盖住，使纸片圆周长总和最短，这些圆周长总和最短是多少厘米？（如图五所示）

教师组织学生讨论“盖住”“纸片周长总和最短”的含义，引导学生理解其中的含义，再类推整圆，解决实际问题，达到拓展规律和运用规律的目的。

第二关：观察比较下图六中阴影部分的面积，你有什么发现？

学生通过观察比较、交流讨论，发现可以把后面三个图转化与第一个图一样，用正方形面积减去圆的面积，剩下的阴影部分面积一定相等。

教师问：“如果正方形里面不是1个圆，而是4个、9个、16个圆，阴影部分面积还是相等吗？”

学生答：“我猜测阴影部分面积是相等的。”

教师问：“怎么验证？需要什么条件？”

学生答：“需要知道圆的半径或直径。”

教师问：“如果正方形边长是12厘米，该怎么算？”

学生答：“只要算出4个圆与9个圆面积之和等于大圆的面积，阴影部分面积就会相等。”（如图七所示）

教师引导学生独立计算小圆面积的和，要求结果还是用“几π”表示，做完后小组交流解题思路，并汇报。

学生说：“都是36π，第二个图中4个小圆的面积之和是π×3×3×4=36π，第三个图中9个小圆的面积之和是π×2×2×9=36π。”

教师说：“现在请你们想象正方形里铺满1个圆、4个圆、9个圆，剩下的阴影部分面积都相等，照这样铺，正方形里面还能铺几个？”

学生1说：“可以一排摆4个摆4排，就是16个。”

学生2说：“还可以摆25个，只要每排摆的个数和排数一样就可以了。”

学生3说：“我认为n2个，因为1×1=1个 ，2×2=4个 ，3×3=9个，4×4=16个，5×5=25个……n×n= n2，所以是n2个。”

总结：根据数量关系S阴=S正-S圆解答，借助数形结合，通过转化、计算或想象得到：因为每個正方形中的白色部分面积（圆的面积）是相等的，所以剩下的面积（如图八所示）也是相等的。

第三关：摆n个三角形，需要几根小棒？每增加一个三角形就增加几根小棒？三角形的个数与小棒的根数有什么关系？你能不能用算式表示图形规律？如图九所示。

学生说：“小棒根数是1+2n或2n+1根。”

教师提问：“‘1+2n中的‘1表示什么？‘2和‘n又表示什么？”

学生答：“算式中的‘1表示第一根小棒，‘2表示每增加一个三角形就增加2根小棒，‘n表示三角形个数。”

教师问：“如果摆n个四边形需要多少根小棒？n个五边形、六边形呢？（如图十所示）”

学生类推得出：摆n个四边形需要小棒1+3n根，摆n个五边形需要小棒1+4n根，摆n个六边形需要小棒1+5n根。

总结：这题先通过数形结合探究简单图形蕴藏的规律，再类推到相类似或相关较复杂的图形中，找到解决这类问题的方法和策略。

全课总结：教师根据学生的汇报，引导学生归纳总结成思维导图。

四、教学思考

这节练习课三个题组的教学有三个共同点：第一，教师引导学生从数形结合的视角经历探究数学规律的过程，归纳规律、解释规律、应用规律，通过解决一个问题，实现了解决一类问题，这就是建模过程;第二，教师通过不断追问，引导学生进行类比，通过联想、猜测，促进学生独立思考和思维碰撞，让知识与方法的迁移发生，这也是推理过程，可以培养学生的推理能力;第三，教师让学生体会“数与形”之间完美结合带来的直观性和简捷性，“形”中蕴含着数的规律，“数”可以用形呈现，体悟数形结合和化繁为简的思想。

笔者原认为这节课内容较难，教学起来会比较吃力，但在实际教学中，学生思维异常活跃。通过观察思考、比较探究、猜想验证、想象推理、交流表达等，学生的思维得到了发散和拓展，也使学生在巩固基础知识和基本技能的基础上掌握了解题的方法和策略，发展了解题能力和学习能力。

（作者单位：广东省佛山市顺德区聚胜小学）