基于图结构的城市道路短时交通流量时空预测模型

王 海 起，李 留 珂，陈 海 波

(中国石油大学(华东)海洋与空间信息学院，山东 青岛266580)

0 引言

精准、实时的城市交通流量预测是城市交通控制和引导的决策基础。交通流量预测可分为短时预测(小于30 min)和长时预测(大于30 min),由于交通流量变化迅速，15 min内的短时交通流量预测更能满足现实生活需求。出租车作为城市出行中较为重要的交通工具之一，其装备的车载GPS可收集不同时间的精确位置信息，同时，出租车交通数据具有数据量大、时空分布广等特点，可间接反映城市道路的交通状态，因此，该数据可用于城市交通流量预测研究[1]。

传统的交通流量预测多采用基于统计学理论的线性模型，如差分自回归移动平均(Autoregressive Integrated Moving Average，ARIMA)模型及其变体模型[2-5]、线性回归模型[6]及卡尔曼滤波[7]等，该类方法抗干扰性差，对于复杂非线性的交通数据预测精度较低；不少学者基于支持向量机(SVM)[8,9]、小波分析[10,11]、分形理论[12]等非线性模型，针对交通流量预测问题开发出许多变体模型，可适用于短时交通流量预测。近年来，深度学习在文本处理、语音识别等领域展现出优秀的特征学习能力，因此，逐渐尝试使用该类方法提取交通流量数据的时空特性并进行交通流量预测。例如：Zhang等[13]提出DeepST模型，利用多层卷积学习交通流量的空间依赖；Wu等[14]使用CNN捕捉交通流量数据空间特征，使用LSTM捕捉短期变异性和周期性；Lai等[15]提出LSTNet模型，根据周期长度对输入数据维度进行整理，解决传统RNN在较长周期中信息难以传递的问题；Yu等[16]结合道路拓扑信息，采用图卷积和一维卷积相结合的方式预测交通流量。以上深度学习模型采用不同模块分别捕捉交通流量数据的时间特性和空间特性，相对于传统交通流量预测模型预测精度有一定提升，然而，现有深度学习模型未考虑城市交通流量数据在时间上的周期性、邻近性和趋势性。因此，本文提出一种基于注意力机制的GC-GRU时空预测模型，采用网络距离构建城市路网结构，按照周期划分历史输入，并利用图卷积(Graph Convolution，GC)和门控循环神经网络分别捕捉空间依赖性和时间依赖性，结合注意力机制对城市道路交通流量进行预测。该模型与ARIMA、SVM、GRU、GCN等常规预测模型相比，考虑了交通流量数据的时空特征信息，与DeepST、STGCN等模型相比，考虑了时间周期性和趋势性。

1 STGCGRU模型

1.1 总体架构

依据交通流量的时空特性，本文构建了时空图卷积门控循环网络预测模型(Spatial-Temporal Graph Convolution Gate Recurrent Unit Network，STGCGRU)进行城市道路交通流量短时预测。模型整体采用Encoder-Decoder架构[17](图1)，由多层图卷积(GC)和门控循环单元(Gate Recurrent Unit，GRU)组合作为GC-GRU基本单元构成单层循环网络，以捕捉交通流量数据的时空特征，并添加注意力机制，动态调整Encoder过程中输入的历史时段中不同单位时间步长(以下简称“时间步”)的权重，以适应交通流量数据的趋势变动性。其中，Encoder部分将多个历史时间步的交通流量数据x1,x2,…，xt输入模型进行编码，并汇总成代表历史输入序列的特征向量ht；Decoder部分对该特征向量进行解码，根据上一时间步隐藏状态及预测结果逐步输出未来时间步的预测结果ht+1,ht+2,…，ht+p；注意力机制部分根据待预测时间步分配各历史时间步权重，然后加权计算上下文信息并与Decoder预测结果融合作为最终预测结果。

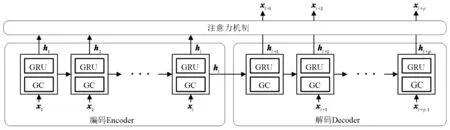
图1 STGCGRU模型总体架构Fig.1 Framework of STGCGRU model

1.2 问题定义

本文将城市路网中的路段抽象为节点V={vi|i=1,2,3,…,n}，路段间的连接关系定义为边E={(vi,vj)|vi∈V,vj∈V}，则城市路网形成无向图G=(V,E,A)，其中A为道路拓扑图结构的邻接矩阵。结合图结构的交通流量预测问题可看作依据历史时段的路段交通流量及道路拓扑图预测未来某时段的交通流量，即存在学习映射函数f，使得：

[xt+1,xt+2,…，xt+p]=f(x1,x2,…,xt,G)

(1)

式中：x1,x2,…，xt为不同历史时间步所有路段节点的交通流量数据；xt+1,xt+2,…，xt+p为所预测的未来p个时间步所有路段节点的交通流量。

1.2.1 道路图邻接矩阵构建 对于城市交通而言，节点间距离越近，其空间相关性越强，因此，本文采用反距离加权方式构建邻接矩阵A(式(2))，两节点间的距离可通过欧氏距离、网络距离、交叉口距离3种方式计算。其中，欧氏距离dist(vi,vj)用于衡量vi与vj两节点间的绝对距离(式(3));网络距离是指出租车在实际行驶过程中起点到终点的最短行驶距离，本文中的网络距离由百度最短路径API求得(图2);交叉口距离为起点到终点经过的最少交叉口数量,如图3所示，两个路段间的交叉口距离为3。

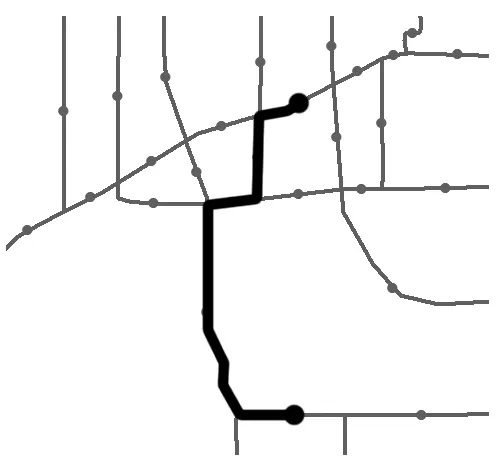
图2 网络距离示意Fig.2 Schematic diagram of network distance

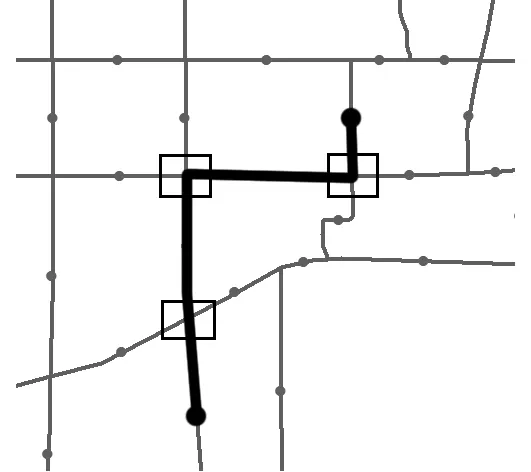
图3 交叉口距离示意Fig.3 Schematic diagram of intersection distance

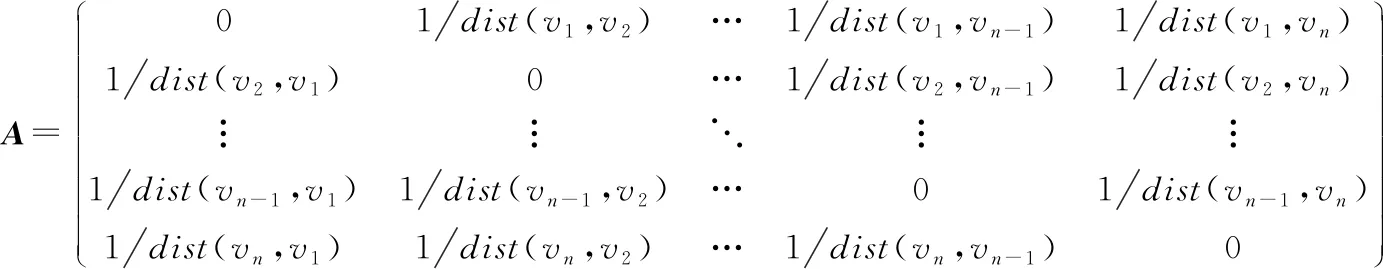
(2)

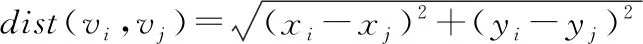
(3)

式中：(xi,yi)、(xj,yj)分别为节点vi、vj的坐标。

1.2.2 历史输入时段划分 考虑城市交通流量数据的时间邻近性、日周期性、周周期性等特点，将输入历史时段{x1，x2,…，xt}划分为邻近片段、日周期片段、周周期片段3部分，每部分长度均为l=t/3。如图4所示，设单位聚合时段为5 min，预测时段为2020年5月20日9:00-9:10的交通流量(即p=2)；输入历史时段每部分片段长度为20 min(即l=4)，则邻近片段为与预测时段相邻的长度为l的时段{xt-l，xt-l+1,…，xt}，即2020年5月20日8:40-9:00；日周期片段为一天前同时段及前后时段，长度同为l，记为{xt-2l-1,xt-2l,…，xt-l-1}，即2020年5月19日8:55-9:15；周周期片段为一周前同时段及前后时段，长度同为l，记为{x1,x2,…，xt-2l-2}，即2020年5月13日8:55-9:15。

图4 历史输入时段划分Fig.4 Division of historical input periods

1.3 GC-GRU单元

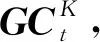
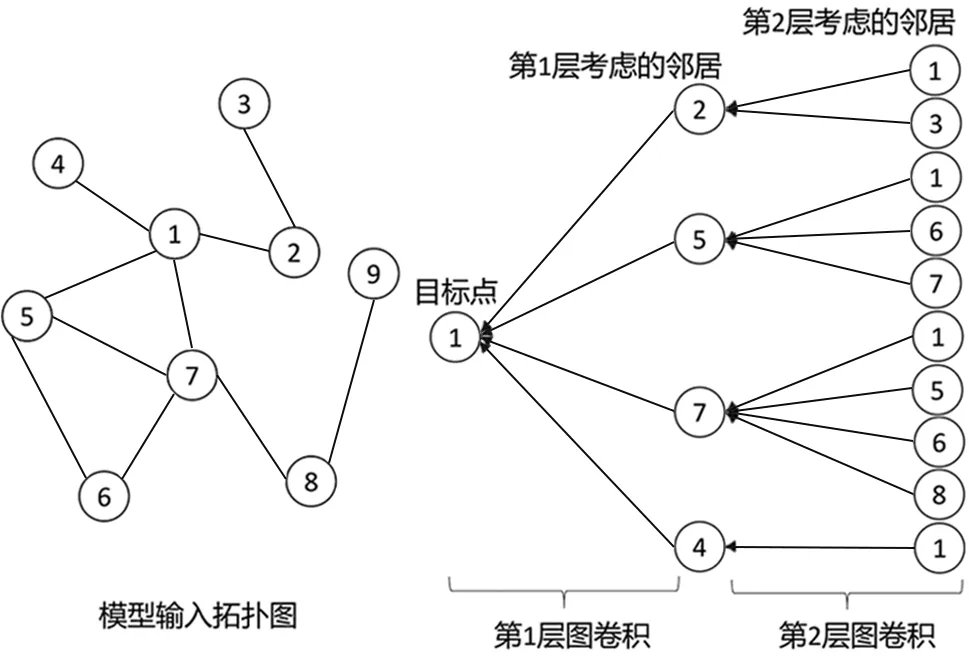
图5 多层图卷积过程示意Fig.5 Schematic diagram of multi-layer graph convolution process

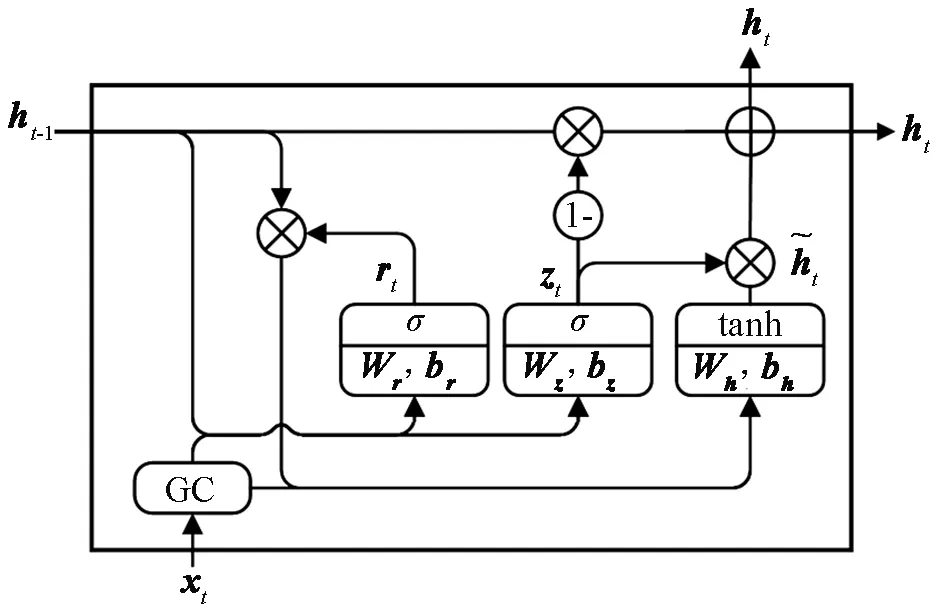
图6 GC-GRU单元内部结构Fig.6 Internal structure of GC-GRU unit

(4)

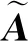
(5)

(6)

(7)

(8)

式中：⊙表示元素相乘；Wz、bz、Wr、br、Wh、bh为可学习的权重矩阵，模型可自动调整当前时刻信息和历史信息的保留比例，保证提取的特征向量ht既包含足够的当前时刻信息，又包含历史信息中的变化趋势。

1.4 注意力机制

注意力机制最早被用于调节权重大小，使模型在关键位置有较高关注力。本文模型中注意力模块[20]可使模型在训练过程中动态调整不同时间步的权重大小，以捕捉交通流量的趋势变动性，具体实现过程为：针对Decoder部分预测的每个时间步ht+Δt，计算Encoder部分所有历史时间步的权重，加权求和得到综合信息cΔt(式(9)-式(11))，再将其与经过GC-GRU单元后的隐藏状态ht+Δt融合作为输出，得到xt+Δt(式(12))。

(9)

(10)

(11)

xt+Δt=tanh(Wc[cΔt,ht+Δt])

(12)

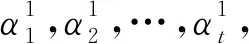
图7 注意力机制详细框架Fig.7 Detailed framework of the attention mechanism

2 实验设置

2.1 实验数据概况

实验数据为北京市五环内2015年5-6月共47天33 234辆出租车产生的GPS轨迹点数据，选择前35天作为训练数据，后12天为测试数据。剔除冗余数据和漂移数据；对于定位偏差数据，采用基于隐形马尔可夫模型的地图匹配算法[21]，将实际GPS轨迹点映射到实际路网中。

以道路交叉口分割的方式，将路段抽象为节点(图8)，共抽取北京市五环内639个路段，平均长度为1 772 m。以路段中点表示路段位置，以5 min为单位聚合出租车轨迹点数量作为该点的交通流量数据。由北京市工作日/周末不同峰期交通流量分布情况(图9，彩图见封2)可知，交通流量多集中在三环内的中关村、三里屯、北京东站附近，出租车多在80辆以上，三环以外路段多在20辆以下。工作日相对周末、早(午)高峰相对晚高峰交通流量整体偏大，具体表现在：工作日早高峰居民出行多为上下班，交通流量较大并集中在北京城区西北部的中关村、西直门、北京西站附近，晚高峰居民出行多为休闲社交活动，交通流量集中在北京城区东部的工体、CBD、劲松桥附近；周末早高峰居民出行较少，交通流量明显偏低，午(晚)高峰交通流量集中在住宅区及休闲娱乐场所较多的工体、CBD、劲松桥等位置附近。

图8 路网抽象为节点Fig.8 Road sections abstracted as nodes in road network

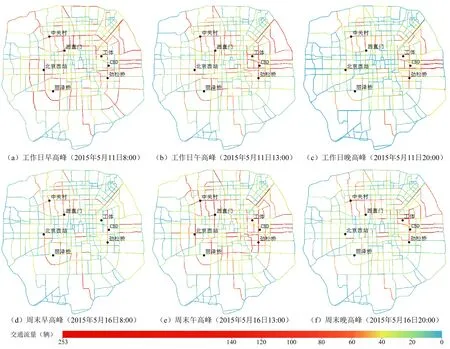
图9 北京市出租车5 min路段聚合交通流量概况Fig.9 General situation of the aggregate taxi traffic flow in Beijing within 5 minutes

以8:00-8:15时段为基础，与其他7个时段交通流量进行Pearson相关分析(图10a),可以看出，8:00-8:15时段与8:15-8:30时段交通流量相关性最高，且相关系数随时间推移逐渐减小，说明交通流量具有时间邻近性；由图10b可知，交通流量呈现日周期性和周周期性；由图10c可知，单日交通流量存在早、午、晚3个高峰，且每日3个高峰的时间和峰值并不完全一致，交通流量数据具有趋势变动性；全局Moran′sI指标可以度量城市路网交通流量的空间自相关性[22]，由不同行驶距离下工作日早高峰时段交通流量的全局Moran′sI指标(图10d)可知，Moran′sI均大于0且逐渐降低，说明交通流量在空间上存在显著的正相关且相关性随行驶距离增长而减弱。

2.2 评价指标及实验参数设置

实验采用的评价指标有均方根误差(RMSE)、平均绝对误差(MAE)、决定系数(R2)，RMSE和MAE越小、R2越大，预测效果越好。公式如下：

(13)

(14)

(15)

STGCGRU模型超参数主要包括图卷积层数、隐层单元数目、输入历史序列长度、图构建方式、学习率及批次大小。实验设置学习率α=0.001，批次大小batchsize=64，随机选取数据集的80%作为训练集，剩余20%作为验证集，模型训练均采用Adam算法进行优化并在模型训练时采用早停策略。1)由图10d可看出，交通流量的空间自相关性在2～4 km处下降较快，结合路段平均长度可认为，交通流量与其2阶以内邻居路段的相关性较强，因此采用2层图卷积捕获交通流量的空间特性。2)日常出行往往优先考虑行驶距离最短的路线，与网路距离计算方式相符，基于网络距离构建的邻接矩阵更适合城市交通拓扑图构建与交通流量预测，因此模型最终选择网络距离作为图构建方式。3)隐层单元数目关系着模型计算过程中传递的信息量，是模型的重要参数之一。由不同隐层单元数目下模型测试误差(图11a)可知，模型RMSE和MAE在隐层单元数目为16时最低，因此选择隐层单元数目为16作为后续实验参数。4)输入的历史序列越长，其承载的信息量越多，但过长的历史序列距预测序列较远，相关性较低，反而会影响模型精度。本文将组成输入的片段时间长度分别设置为15 min、25 min、35 min、45 min、55 min，即总输入历史序列长度T分别为9、15、21、27、33，分别计算模型RMSE和MAE(图11b)，可以看出，在片段时间长度为35 min，即输入历史序列长度为21时，RMSE和MAE均达最低，故最终选择输入历史序列长度为21。

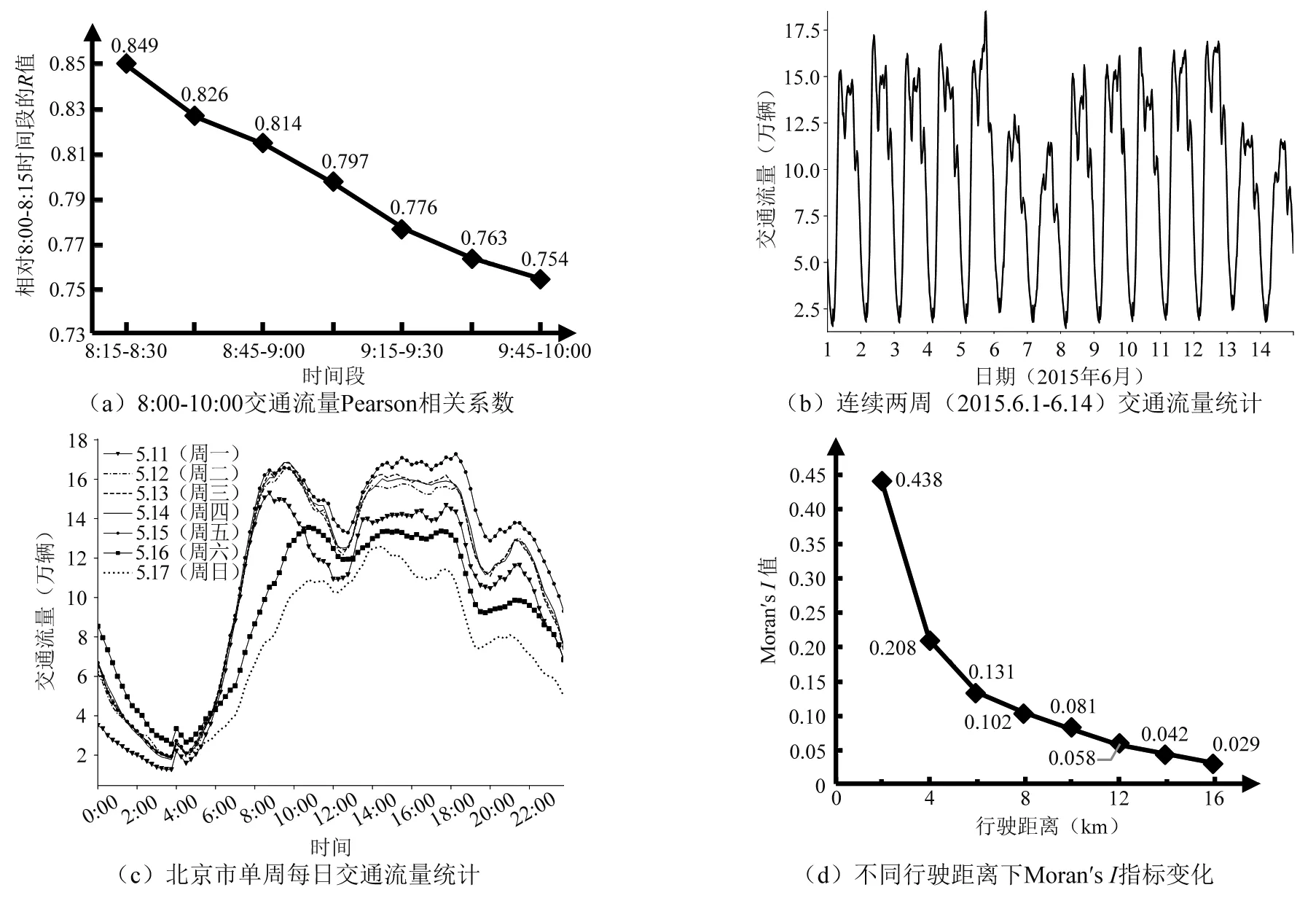
图10 北京市出租车交通流量时间特性分析Fig.10 Analysis of time characteristics of taxi traffic flow in Beijing

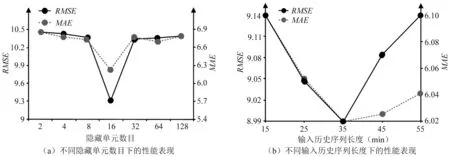
图11 模型参数选择Fig.11 Parameter selection for the model

3 结果分析

3.1 模型对比分析

为验证本文模型的可靠性，选取以下5种交通流量预测模型进行对比分析： 1)差分自回归移动平均(ARIMA)模型，是一种经典的时间序列预测模型；实验中采用ARIMA(1,1,1)模型，即差分次数、自回归项和移动平均项均为1。2)支持向量机(SVM)模型，利用核函数实现输入数据到高维特征空间的映射，分析输入输出间的非线性关系；实验中采用的核函数为高斯核函数，惩罚系数设置为0.1，γ为0.01。3) GRU模型，实验中设置隐藏层数为2，每层的隐藏单元数目均为16。4)GCN模型，实验中设置图卷积层数为2，每层的神经元数目均为16。5)深度时空残差神经网络DeepST，对时刻、天、周3段数据分段采样，分别采用多层残差神经网络并利用全连接融合，相对于原始DeepST模型[13]，无额外因素模块。ARIMA、SVM、GRU、GCN 4个基准模型均采用与预测目标时间邻近的前35 min(即前7个时间步)的历史交通流量作为输入，为保证模型输入一致及对比公平性，实验采用不包含周期片段输入的STGCGRU模型(输入同为前7个时间步)与基准模型进行对比，采用带有周期性的STGCGRU模型与同样包含周期性的现有DeepST模型进行对比。

由不同模型的RMSE、MAE、R2(表1)可以看出：1)在相同输入时间长度下，未加周期片段的STGCGRU模型相对传统的交通流量预测模型(ARIMA、SVM)而言，RMSE分别减少了69.69%和52.92%，MAE分别减少了70.23%和43.93%，R2分别提高了56.14%和41.27%，说明STGCGRU模型能更好地映射交通流量数据中的非线性关系，捕捉交通流量数据的趋势变动性，预测精度较高。未加周期片段的STGCGRU模型的RMSE比GRU和GCN分别减少了6.88%和6.67%，MAE分别减少6.89%和7.34%，R2均提升了5.95%，说明STGCGRU模型可较好捕捉时空特性。2)DeepST模型预测误差低于基准模型，而STGCGRU模型的3种评价指标仍优于DeepST模型，说明采用多层图卷积比多层卷积能更好捕捉道路的空间特征。3)对比保留周期片段和不保留周期片段的STGCGRU模型预测结果可以看出，将日周期和周周期片段加入模型输入序列，对模型预测精度有提升效果，故考虑周期性对交通流量预测至关重要。

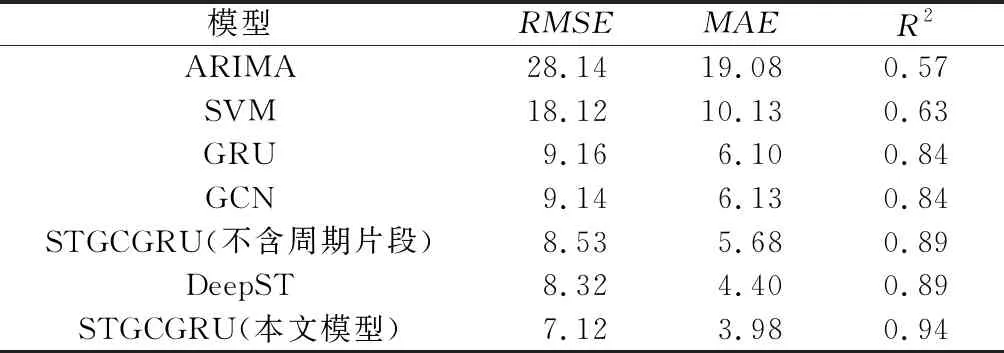
表1 不同模型对北京市出租车交通流量时间特性的预测精度Table 1 Prediction accuracy of time characteristics of taxi traffic flow using different models in Beijing

由STGCGRU模型在不同预测时长下的预测结果(表2)可知，随着预测时长增加，RMSE和MAE均呈上升趋势，R2呈下降趋势。可能是由于在Decoder部分上一步输出参与到下一步预测的计算造成误差累积，从而导致模型误差随预测时长增加而增大，说明STGCGRU模型较适合短时交通流量预测。

表2 不同预测时长下STGCGRU模型交通流量预测精度Table 2 Prediction accuracy of traffic flow using STGCGRU model under different prediction duration

3.2 不同交通情况下预测结果分析

人们在日常出行中更在意高峰期的交通拥堵状况，因此本文利用STGCGRU模型对工作日和周末高峰时段的真实数据进行测试，其中早高峰为8:00-11:00，午高峰为13:00-16:00，晚高峰为19:00-22:00。由于真实数据缺失天数较多，很难满足周周期、日周期所对应日期数据的真实性，因此实验中采用未加周期片段的STGCGRU模型，训练及测试数据均为有缺失时段的真实数据。同时，添加全时段预测结果作为基准对比，输入时间序列长度为35 min，预测时长为5 min，预测结果如表3所示。整体而言，全时段由于包含车流量基本为0的凌晨时段，预测结果较好。工作日相对周末交通流量基数大，因此工作日预测结果的RMSE和MAE相对周末高，而反观R2，工作日相对周末高，主要是由于工作日交通流量规律性较强。对比早高峰、午高峰、晚高峰3个时段，晚高峰模型预测结果在工作日和周末均较好，震荡较为明显的午高峰预测结果较差。

表3 STGCGRU模型在高峰时段预测结果对比Table 3 Comparison of prediction results of STGCGRU model during peak hours

易堵路段同样是交通流量预测的关注重点。对车流量较大的中关村在工作日和周末的交通流量进行预测，并与真实值进行对比(图12)。中关村作为教育、科技聚集地，在工作日上下班时段交通流量大，晚高峰较为明显，在周末各时段交通流量较为平均。从图12可以看出，STGCGRU模型可较好地拟合交通流量的趋势，对于交通流量变化平稳时段预测结果较精准，对于交通流量突增或突减情况，预测值与真实值存在一定的偏差。

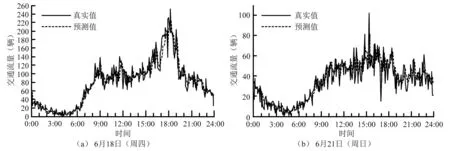
图12 易堵路段预测值和真实值对比Fig.12 Comparison of predicted values and actual values in easily blocked road section

4 结论

本文提出一种基于注意力机制的交通流量时空预测模型——STGCGRU模型，该模型采用Encoder-Decoder结构，结合图卷积和门控循环单元捕捉交通流量的时空特性，利用注意力机制调节趋势变动性和周期性对预测的影响。基于北京市出租车交通流量数据集，与ARIMA、SVM、GCN、GRU基准模型及DeepST模型对比后发现，STGCGRU模型可以捕捉交通流量数据中的时空特征，预测精度更高；将STGCGRU模型应用于不同时长的交通流量预测，发现该模型更适合城市交通流量短时预测；结合不同交通情况分析发现，工作日相对周末模型拟合效果更好，早晚高峰相对午高峰预测结果更好。STGCGRU模型对于交通流量趋势捕捉较为敏感，有助于揭示短时段内交通状况，为城市智能交通决策提供参考。但该模型不能立刻捕捉交通流量突变情况,未来将添加天气、交通事件等导致交通流量突变的其他因素，以提高模型对交通流量突变情况的预测精度。