振荡波电压作用下的电缆介质损耗测量方法

徐小龙， 李波， 卢雨欣， 张航伟， 曾祥峰

(1. 西安交通大学电气工程学院，陕西 西安 710049；2. 国网江苏省电力有限公司营销服务中心，江苏 南京 210036；3. 国网湖南省电力有限公司长沙供电分公司，湖南 长沙 410015)

0 引言

随着电网的发展，电力电缆凭借其良好的电气性能在电力系统中得到了大规模的应用。随着运行年限的增加，电缆本身会出现不同程度的绝缘老化现象，对电网造成威胁。因此，保障电力电缆的安全、稳定运行具有重要意义。介质损耗可以表征电缆整体的绝缘水平，通过对电缆进行介质损耗检测，对其变化趋势进行分析，能够有效评估电力电缆绝缘的性能、寿命等[1—4]。

早期的介质损耗测量实验一般采用西林电桥，但其输出功率不能满足大容值试品的测试要求，具有使用局限性[5—7]。在现场测试中，一般通过测量设备上的电压与流过自身电流相位差实现介质损耗角的测量，但是该类方法的后处理算法均存在较大误差[8—9]。例如，频谱分析法由于频谱泄露和栅栏效应，导致求解得到的电压与电流相位有较大误差[10—12]；相关系数法由于环境噪声干扰，得到的相位差的准确度具有随机性；正弦波参数法无法准确得到基波频率，导致所拟合函数与实际波形有较大偏差，从而产生较大误差[13—15]。

目前介质损耗能采用单一频率或扫频方式进行测量，通过检测、记录固定频率下容性试品的介质损耗，可得到容性试品的绝缘状态变化趋势，从而及时发现绝缘状态异常情况并采取相应的补救措施。单一频率一般采用50 Hz，扫频方式的频率一般为0.1～1 000 Hz[16]。

振荡波测试系统(oscillating wave test system，OWTS)由于其便携性、经济性、等效性好，目前在电气设备状态检测领域得到了较好的应用，但是振荡波系统开展的工作主要针对局部放电领域，暂未集成介质损耗测量功能[17—19]。

为了解决上述方法、系统的局限性，文中提出了基于OWTS的介质损耗测量方法，即结合振荡波测试过程中采集到的电压波形或电压、电流波形的数据计算得到介质损耗，并对这2种计算方式和应用场景进行分析对比。

1 OWTS原理

OWTS主要分为2种，分别为直流OWTS和交流OWTS，文中以直流振荡波为例，介绍振荡波结构以及产生过程。

传统直流OWTS的步骤和结构如图1、图2所示，主要由市电输入、整流滤波电路、变频系统、升压变压器、倍压电路、振荡波转换开关、控制和采集单元、电感以及容性试品构成。直流OWTS主要步骤为：(1) 系统通过市电供电，将市电整流、滤波后变成直流电；(2) 直流电经变频系统逆变成倍压电路所需的电源频率；(3) 逆变后的电源经升压变压器、倍压电路升至理想电压后，通过控制单元关闭充电开关S2、打开振荡波转换开关S1，形成振荡衰减的电压波形，具体波形如图3所示。

图1 OWTS步骤Fig.1 Steps of OWTS

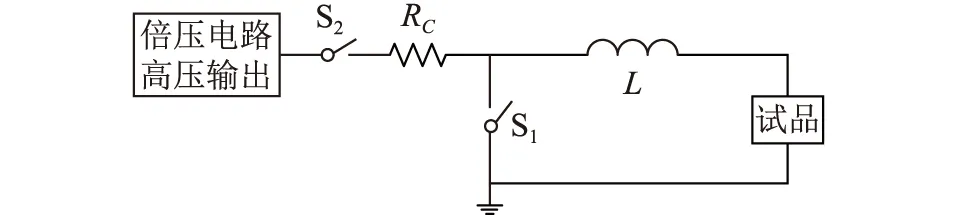
图2 OWTS结构Fig.2 Structure diagram of OWTS

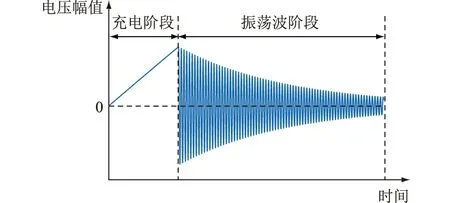
图3 OWTS工作波形Fig.3 Working waveform of OWTS

2 振荡波技术在介质损耗测量中的应用

2.1 介质损耗测量原理

介质损耗是高压容性设备状态评估的一项重要指标。由于电缆导体与屏蔽层形成两极，导致电缆整体呈容性，因此测量介质损耗可以对电缆绝缘状态进行评估。理想的电力电缆的电压相角超前流过自身的电流相角90°，但实际情况难免有泄漏损耗、极化损耗导致相位差小于90°。

介质损耗一般采用电容与电阻并联或串联的等效电路来表示，文中以并联形式举例说明，如图4(a)所示。其中，Ceq，Req分别为容性设备的等效电容与等效电阻。为了更好地理解介质损耗角的物理意义，将流过等效电容、电阻的电流用矢量图形式表示，如图4(b)所示。其中，φ为电压U与电流I的相位差；δ为介质损耗角。

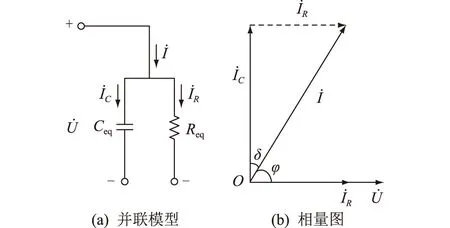
图4 介质损耗并联模型与相量图Fig.4 Dielectric loss parallel model and phasor diagram

结合图4，可得并联等效电路下的介质损耗角正切值数学表达式如下：

(1)

2.2 基于振荡波电压波形的介质损耗角测量

振荡波产生时的电路如图5、图6所示。其中，L为电感；R1为系统等效电阻；C为电容试品的等效电容；R2为电容试品的等效电阻。振荡波转换开关闭合后，原本充到预设电压的电容试品与电感组成振荡回路，由于系统电阻、泄露电阻的存在形成逐渐衰减的振荡波。由直流振荡波的工作方式可得，待电容两端电压升至预设电压后，将会断开电源侧，同时电路结构为RLC电路，因此振荡波过程属于二阶零输入响应。

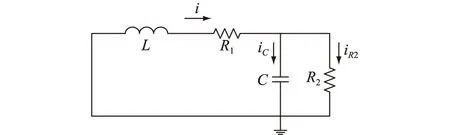
图5 振荡波过程电流走向Fig.5 Oscillating wave current trend graph

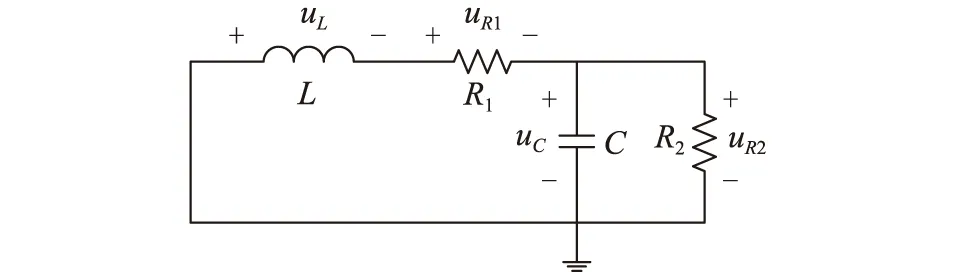
图6 振荡波过程电压分布Fig.6 Oscillating wave voltage profile

由基尔霍夫电压、电流定律可得：

i=iC+iR2

(2)

uL+uR1+uC=0

(3)

其中：

(4)

(5)

uR1=iR1

(6)

(7)

联立方程可得：

(8)

解得：

uC(t)=U0e-λt(cosωt+αsinωt)

(9)

式中：U0为容性试品振荡波的起始电压。

(10)

(11)

(12)

结合式(1)和式(11)，可得：

(13)

结合上述公式推导，得到了基于振荡波电压波形的介质损耗角正切值计算公式，在实际 tanδ测量过程中，通过分压器测得电容试品的振荡波电压波形，然后通过波形分析，得到波形角频率ω以及波形的衰减系数λ，同时电感L，系统等效电阻R1为已知参数，代入式(13)即可得到 tanδ。

2.3 基于振荡波电压和电流波形的介质损耗角测量

由2.2节的结果可得，电容两侧电压为：

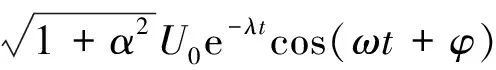
(14)

其中：

tanφ=-α

(15)

回路总电流可表示为:

(16)

其中：

(17)

(18)

结合式(1)与式(18)可得：

(19)

结合上述公式推导，得到了基于振荡波电压、电流波形的介质损耗角正切值计算公式，在实际tanδ测量过程中，通过分压器测得电容试品的振荡波电压波形，通过电流互感器或引入测量电阻测得回路总电流波形，对采集到的电压、电流波形进行波形分析，得到电压与电流的相位差θ，波形角频率ω以及波形的衰减系数λ，代入式(19)，即可得到 tanδ值。

2.4 振荡波电压下的介质损耗判断标准

振荡波频率一般为20～500 Hz，由文献[20]可得不同频率下实际的介质损耗不同，因此不可按照工频下的介质损耗检测标准判断试品的绝缘状态。介质损耗实际表征试品的绝缘状态，频率只是影响介质损耗的绝缘状态判断标准，因此振荡波下的介质损耗测量可以针对同一试品建立介质损耗档案，通过介质损耗变化趋势评判试品的绝缘状态，或者参考超低频正弦波电压测量标准，对频率进行分段，并设置相应频段的介质损耗判断标准[21]。

3 介质损耗测量仿真分析

基于Matlab中Simulink模块搭建仿真平台，对上述2种测量方法进行验证。以直流振荡波为例进行说明，Simulink电路如图7所示。

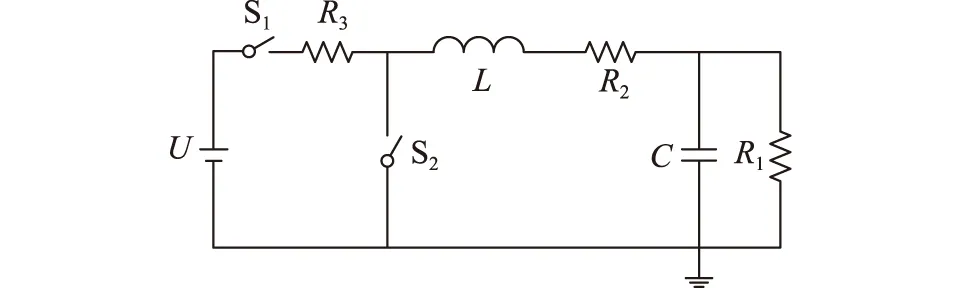
图7 仿真模型Fig.7 Simulation model

图7中，U为高压直流源；S1为充电开关；R3为充电电阻；S2为振荡波开关；L为电抗器；R2为系统等效电阻；C为试品等效电容；R1为试品等效电阻。参数设置如下：高压直流电源U充电电流为20 mA；R3为10 kΩ；L为4 H；R2为25 Ω；C为200 nF；R1为20 MΩ。仿真控制方式为：首先，断开S2开关、闭合S1开关，高压直流电源U以20 mA电流恒流充电，待试品电容两侧电压升到预设电压U0时，断开S1开关、闭合S2开关，试品电容、电抗器组成振荡回路，产生振荡衰减的电压波形，同时，采集振荡波期间试品电容两侧的电压以及回路总电流。

3.1 试品介质损耗角正切真实值

对于系统振荡频率，由于电容两侧并联阻抗较大，对振荡频率影响较小，故忽略不计。振荡时，电路图可简化为图8。

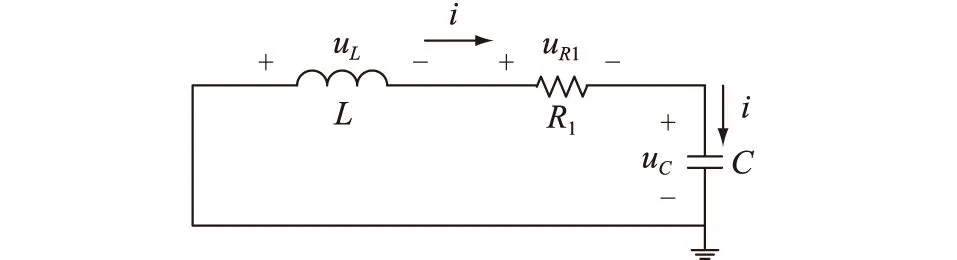
图8 简化电路Fig.8 Simplified circuit

列写微分方程求解振荡频率：

uL+uR1+uC=0

(20)

(21)

联立方程可得：

(22)

由于振荡波过程属于欠阻尼状态，可得：

(23)

则uC可表示为：

uC=eαx(C1cosωt+C2sinωt)

(24)

其中：

(25)

(26)

结合参数设置，可得振荡频率与试品介质损耗角正切真实值为：

(27)

(28)

3.2 基于振荡波电压波形仿真处理

从Simulink模块中提取振荡波过程中电压波形，如图9和图10所示。

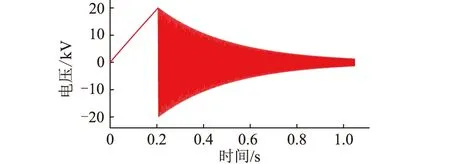
图9 振荡波电压波形Fig.9 Waveform of oscillation wave voltage

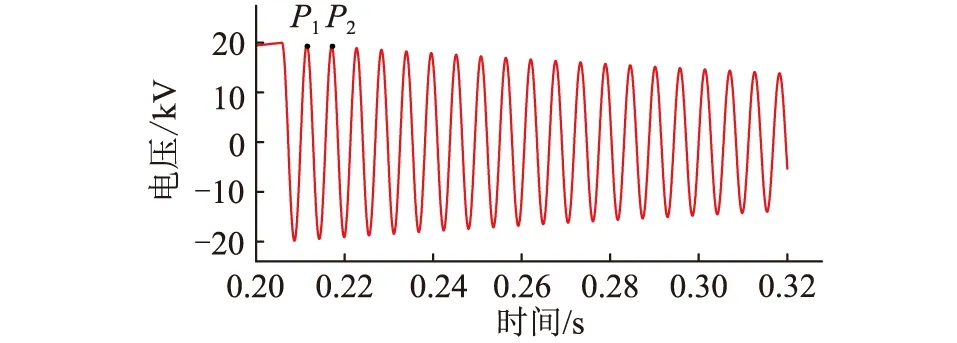
图10 振荡波局部电压波形Fig.10 Waveform of oscillation wave local voltage

选取P1与P2点计算衰减系数以及角频率，可得：

(29)

误差为：

(30)

式中：ω为1 118.03 rad/s；λ为3.250。

3.3 基于振荡波电压、电流波形仿真结果分析

从Simulink模块中提取振荡波过程中试品电压以及回路总电流波形，如图11所示，衰减系数以及角频率可以从电压或电流波形直接得到，电压、电流相位差可通过极值点相位比较法或过零点比较法得到，图11为极值点相位比较法。

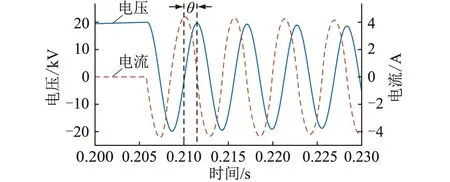
图11 振荡波电压和电流波形Fig.11 Waveforms of oscillation wave voltage and current

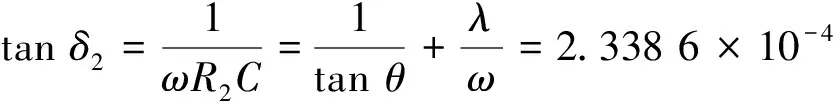
(31)

误差为：

(32)

式中：θ为90.153 2°。

改变试品电容两端并联电阻的阻值，重复多组试验，试品电容均为200 nF, 结果见表1。

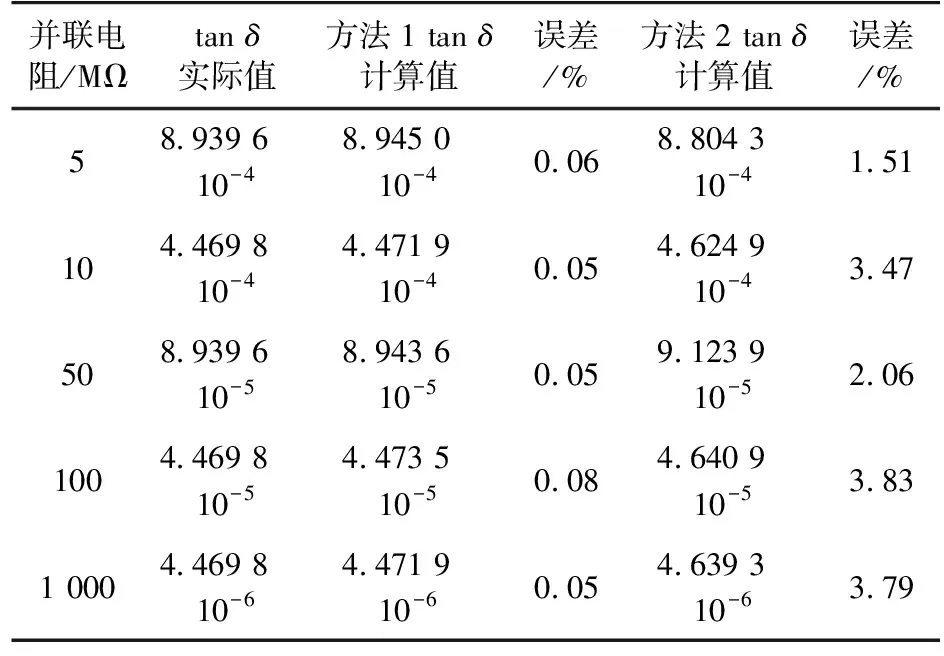
表1 不同并联电阻处理结果Table 1 Data error comparison between two methods

其中方法1为基于振荡波电压波形方法；方法2为基于振荡波电压、电流波形方法。误差均在允许范围内，同时对比不同并联电阻下的介质损耗正切值，介质损耗正切值随并联电阻的减小而增大，与实际情况相符，验证了2种方法可以对不同绝缘状态下的试品进行评估。

3.4 测试方法对比与现场误差分析

3.4.1 参数变化

基于振荡波电压波形的介质损耗角测量方法在求解过程中，默认电感L,系统等效电阻R1是一组已知量。振荡波设备出厂时，铭牌上有较为准确的L,R1，实际计算中可代入公式求解。

查阅文献资料可得，在不同电流、频率下，电感L,电阻R1会有变化，会偏离铭牌上所标的值[22—23]。同时，电阻R1也会随现场温度改变，因此基于振荡波电压波形的介质损耗角测量方法在现场有较大的局限性。

基于振荡波电压、电流波形的介质损耗角测量方法在求解过程中，所需要的参数均为波形后处理得到，因此不会受到现场条件影响，具有较高的准确性以及实用性。

3.4.2 测量误差

试验过程中，噪声是影响tanδ测量准确度的一项重要因素，一般通过数字滤波方法对采集到的原始波形进行初步处理。噪声一般为高频信号干扰或工频信号耦合到信号采集卡中。因此，在数据处理过程中，可以通过设置带通滤波的方式将噪声滤除。

振荡波系统的分压器根据不同情况选取不同的分压比，一般选用10 000∶1或100 000∶1的变比，因此分压后的值很小，微小的零点漂移对衰减系数λ影响较大，需要对其进行分析。

以y=Ae-λtcosωt+B函数为例，其中，A为峰值高度；B为零点漂移量；λ为衰减系数；ω为信号角频率。选取该函数一段波形进行分析，如图12所示。

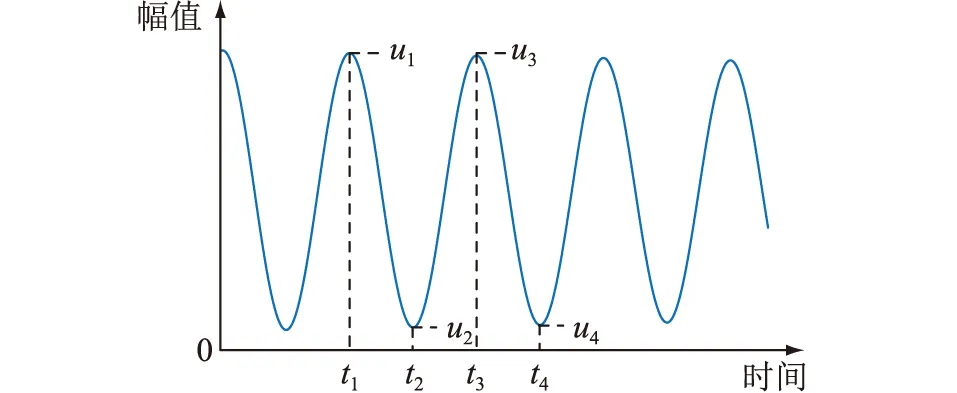
图12 零点漂移分析Fig.12 Zero drift analysis

选取临近的正、负峰值u1，u2，u3，u4，相应的时间为t1，t2，t3，t4，时间间隔为Δt，设u′1，u′2，u′3，u′4为消除零点漂移后的值，可得：

(33)

由于y=Ae-λtcosωt+B为正弦项与指数项相乘所得，正负峰值时的相位并不为0或π/2，但是两相邻的正峰值或负峰值的时间差均为整周期时间T，即峰值偏移相同的相位φ，故峰值处的幅值的基本项Acosφ、Acos(φ+π/2)用±C来表示，文中不再进行证明。

(34)

式中：u1，u2，u3，u4，Δt均为已知量，可以将e-λΔt替换为x，则式(34)可转换为式(35)，便可精确求出 λ，如式(36)所示。通过此算法可以弥补零点漂移带来的误差。

(35)

(36)

4 介质损耗测量实验验证

为了验证基于振荡波电压的介质损耗测量方法的有效性，在实验室搭建了实验平台，其原理如图13所示。

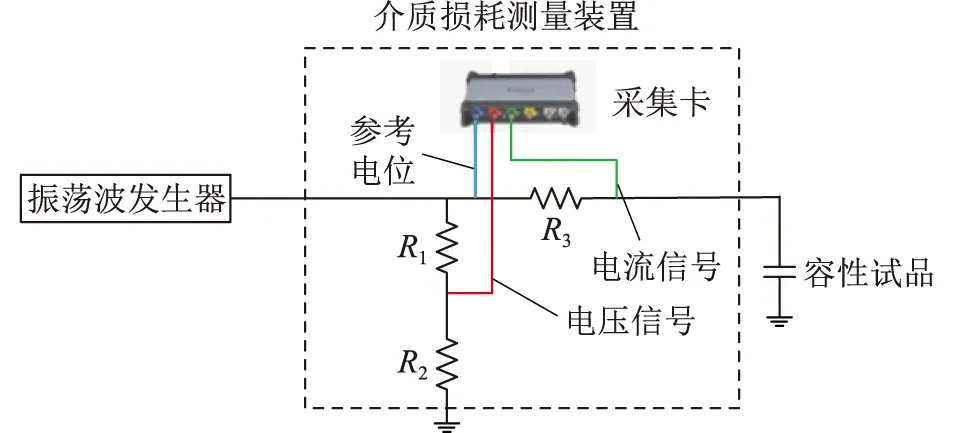
图13 实验平台原理Fig.13 Experimental platform schematic

其中，电压与电流采集部分集成在介质损耗测量装置里，电压采用电阻分压器提取，电流通过测量串入0.1 Ω 无感电阻上的电压间接测量回路电流；容性试品为4组 0.5 μF 的电容，选取单组和2组、3组、4组并联组成容值分别为0.5 μF，1 μF，1.5 μF，2 μF的试品作为研究对象；并联电阻选取无穷大电阻(即不并联电阻)，500 MΩ，50 MΩ模拟不同绝缘状态。依据上述参数进行实验，设置峰值电压为18 kV，使用基于振荡波电压、电流波形的介质损耗测量方法进行计算，结果如表2所示。

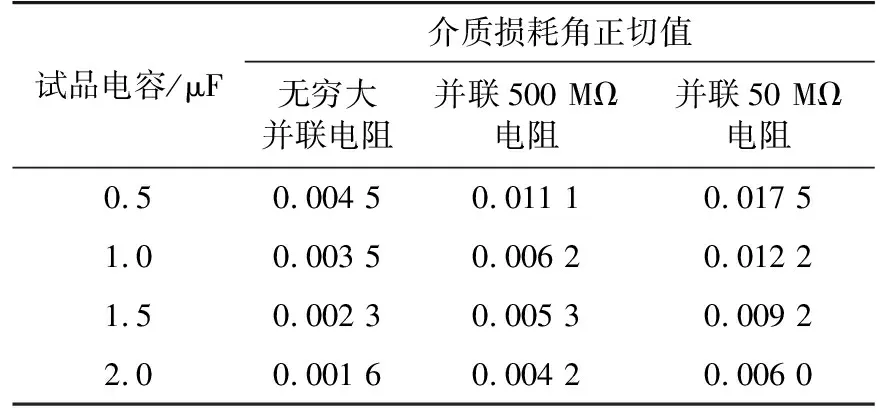
表2 介质损耗测量实验结果Table 2 Dielectric loss experimental results

由表2可得，相同电容容值下，并联电阻越大，计算得到的介质损耗角正切值越小，与实际情况相符合，可验证文中介质损耗测量方法的有效性。

5 结语

目前振荡波测试系统开展的工作主要针对局部放电领域，暂未集成介质损耗功能，针对目前系统的不足，提出了基于OWTS的介质损耗测量方法，采集振荡波期间的电压或电压、电流波形数据，对数据进行后处理得到介质损耗角正切值，实验仿真验证了文中方法的准确性。同时，结合现场测试条件，对2种振荡波下介损测量方法进行对比，得到基于振荡波电压、电流波形的介质损耗角测量方法更适合现场测试，并提出了解决零漂的计算方法，可以提高现场测试结果的精确度。最后，通过实验验证了该方法的有效性。