基于卷积神经网络的N-2线路开断潮流快速计算

刘学华， 孔霄迪

(1. 国电南京自动化股份有限公司，江苏 南京 210032；2. 南京南瑞继保电气有限公司，江苏 南京 211102)

0 引言

近年来，世界范围内发生了多起大停电事故，引起重大的社会经济损失[1—2]，2003年满足“N-1准则”的意大利全网在多个元件相继开断后发生大停电[3]。为此，我国于2019年更新了电力系统安全稳定导则，在静态安全分析的“N-1准则”基础上增补了“N-2准则”的内涵[4]。目前，在满足“N-1准则”的基础上，部分经济发达地区已经实现了N-2校核。然而，随着电网的大规模互联、新能源设备与不确定负荷的大量接入，N-2场景数呈爆炸式增长，传统的交流潮流(alternating current，AC)算法难以满足实际工程的在线潮流计算的需求，其中线路开断尤为突出，为此，有必要研究N-2开断潮流的快速计算方法，当前研究主要分为3类。

其一，并行计算技术在潮流方程的应用包括直接法与迭代法[5]。直接法基于矩阵分解与求逆，不存在收敛问题，但并行化程度较低，通信开支较大，难以应用于大规模系统。迭代法并行化简单，通信开支小，但收敛速度慢，且迭代次数随处理器数目增长而增加[6]。

其二，为减少潮流计算量，有研究对AC算法进行简化，部分计及甚至完全忽略潮流方程的非线性。经典的直流潮流(direct current，DC)算法将非线性潮流方程转化为有功与相角的线性方程求解。然而，DC算法的计算误差通常较大，分析精度尚不足以实现大系统的工程分析，且无法提供电压与无功信息[7—8]。

其三，大量基于人工智能(artificial intelligence，AI)的分类学习技术已应用于电力系统静态安全评估，包括支持向量机、人工神经网络(artificial neural network，ANN)、C4.5等[9—10]。基于大量训练的静态安全AI评估分类准确性高，但研究结果缺乏潮流数据，无法据此配置安全控制措施。对此，前馈神经网络、径向基函数等方法被应用于快速潮流计算[11—12]，然而其成果局限于新英格兰系统，在大系统的强壮性有待校核，相对传统AC算法其速度优势并不显著。近两年，卷积神经网络(convolutional neural network，CNN)已被应用于N-1故障潮流计算[13]，相比传统AC算法，基于CNN的潮流计算速度显著提升，但关于N-2开断的研究依然是空白。

文中基于系统拓扑与工况变化设计原始特征图，应用CNN求解全网潮流，避免了AC算法复杂的非线性代数方程组求解，实现了约80倍的计算速度提升。相比传统ANN，CNN显著减少训练参数，缓解过拟合问题，将计算精度提高了近1个数量级。

1 CNN原理

CNN是一种数据处理的深度学习模型，能由低至高自适应地学习特征的层次结构，常用于处理具有网格属性的数据，譬如图像、语音等[14—15]。该模型包括卷积层、池化层与全连接层，结构如图1所示。其中，实线箭头描述了CNN的训练与应用过程，虚线箭头指向的损失函数计算仅在CNN的训练阶段，用于优化网络参数。卷积层与池化层通常用于进一步从原始特征图中提取信息；全连接层建立特征与目标信息的映射关系并预测输出。

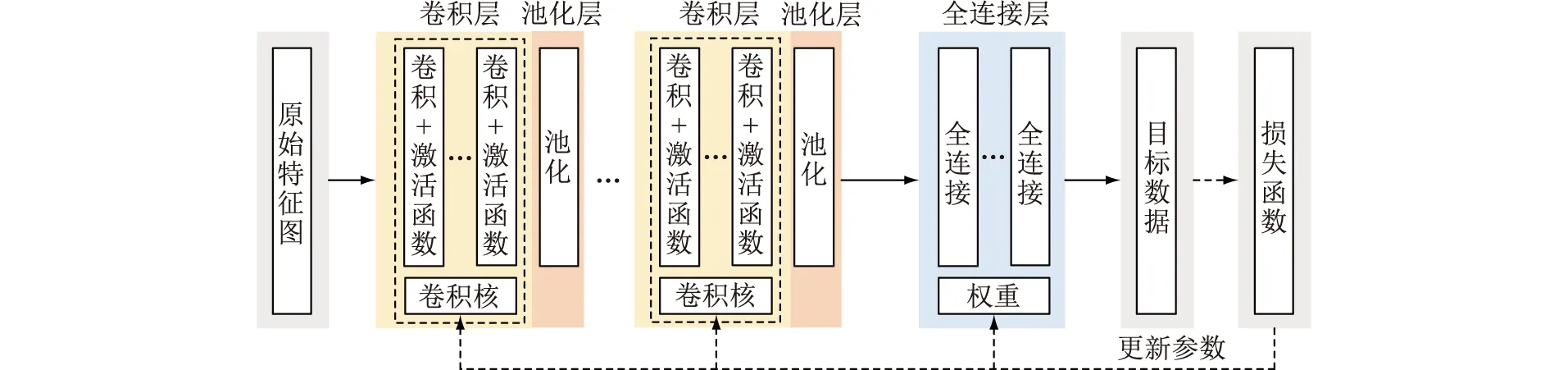
图1 CNN结构Fig.1 Structure of CNN

卷积层利用卷积核进一步提取输入数据的特征，这是CNN区别于其他神经网络的关键。相比传统ANN，卷积计算的引入使CNN具有权值共享与连接稀疏两大特性[16—17]。相比传统的全连接方式，卷积计算显著减少了训练参数，降低了离线训练的计算量，有效缓解了过拟合问题，提高了神经网络的泛化能力。

卷积层的存在使得原始特征图中数据之间可以分组聚合，以电力系统潮流计算为例，传统ANN方法将全部节点信息混合输入，无法实现信息与节点的关联；CNN方法能够按节点对原始特征图求卷积，通过权值共享与稀疏连接避免了大量无关参数参与训练带来的过拟合问题。

2 基于CNN的故障潮流计算

对于n节点系统，其任意节点i的潮流方程如式(1)所示。

(1)

式中：Vi，θi分别为节点i的电压幅值与相角；Pi，Qi分别为节点i的注入有功与无功功率；Gii，Bii分别为节点i的自电导与自电纳。当i与j不等时，Gij，Bij分别为节点i与节点j的互电导与互电纳。式(1)求解的电压幅值与相角即文中所指潮流结果，支路潮流可据电压幅值与相角进一步求解。

基于CNN的线路开断潮流计算包含离线训练与在线应用2个阶段，如图2所示。

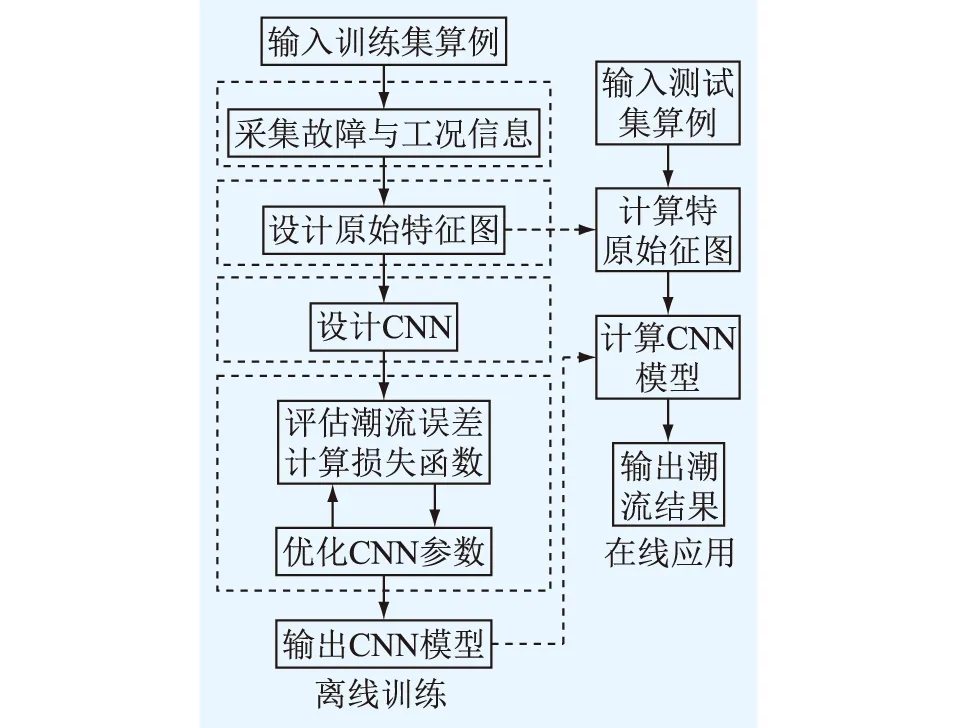
图2 基于CNN的故障潮流计算流程Fig.2 Flow chart of post-contingency load flow calculation based on CNN

在线应用时，对测试集中的具体算例输入原始特征图，根据离线训练的CNN模型，计算故障潮流。离线训练阶段主要包括以下4个模块：

(1) 采集故障与工况信息。针对训练样本算例，采集信息包括初始拓扑的网络参数(电导与电纳)、被开断支路编号、发电机出力与负载。此外，还需基于离线仿真(一般采用AC算法)计算故障后潮流电压幅值VAC与相角θAC，以评估基于CNN的潮流结果误差，计算损失函数。

(2) 设计原始特征图。不同于传统ANN方法，CNN通常以图像类数据为输入信息。采集故障与工况信息后，可将各节点信息构成一张原始特征图，设计过程详见第3章。

(3) 设计CNN。CNN包括卷积层、池化层与全连接层。考虑到式(1)中潮流结果与各节点属性强相关且文中特征图的计算量较小，不再采用池化层进一步缩减特征图信息。综上，文中CNN的设计涉及卷积层(卷积核尺寸、个数，卷积层层数)及全连接层(全连接层层数)。

(4) 基于损失函数优化CNN参数。损失函数用于明确离线训练参数的优化方向。在优化CNN网络的卷积核参数与全连接的权重参数时，文中考虑以潮流计算误差最小为训练目标，而潮流计算误差包括电压误差eV与相角误差eθ两方面。记CNN的故障潮流计算电压幅值、相角分别为VCNN与θCNN，以模块(1)中离线仿真AC算法的电压幅值、电压相角结果VAC与θAC为参考，分别按式(2)与式(3)定义eV与eθ：

(2)

(3)

基于eV与eθ描述损失函数，如式(4)所示。

(4)

式中：αV，αθ分别为电压误差与相角误差的惩罚因子，默认取1。在迭代周期内，根据最小损失函数对应的CNN参数输出离线训练的CNN模型。

3 原始特征图的设计

电力系统潮流计算中，每一节点均具有其对应的拓扑或工况属性，且属性数目常大于1。传统神经网络以向量为输入信号，丢失了节点与属性的对应关系，而在CNN的计算中，原始特征图保留了这种对应关系，且图中的节点属性可采用通道描述。结合卷积本身具有权值共享与连接稀疏的特点，基于CNN的潮流计算结果往往相对ANN精度较高且泛化性能较好。

为了控制计算规模，文中设计了3通道的原始特征图，考虑到各算例的基态相同，取故障前后节点参数的变化量为各通道属性。由式(1)可知，节点电压和相角(Vi，θi)仅与注入功率(Pi，Qi)和导纳(Gij，Bij)有关。考虑到在交流高压电网中，输电线路的电抗要比电阻大得多，电导远小于电纳，文中忽略电纳矩阵中非主对角元与电导矩阵的影响，将n个节点的自电纳变化量构成n×1阶向量作为通道1输入，记为ΔB，该通道特征描述拓扑结构对潮流结果的影响。另外，将n个节点的注入有功功率的变化量形成n×1阶向量，记为ΔP；注入无功功率的变化量形成n×1阶向量，记为ΔQ，分别作为特征图通道2与通道3输入CNN。相应地，将n×1阶节点电压幅值向量V与n×1阶节点电压相角向量θ作为输出信号。

为进一步提高CNN的训练效果，采用min-max标准化方法对原始特征图中信息进行归一化处理，将其线性映射到[0,1]之间，如式(5)所示。

(5)

式中：x*为归一化后的特征数值；x为原始特征数值；xmin，xmax分别为特征最小、最大值。

上述原始特征图的数据量是节点数的3倍，给卷积神经网络带来的训练负担小，对大规模系统的潮流计算具有实用性。

4 CNN的设计

文中CNN由2个卷积层与1个全连接层构成，如图3所示。

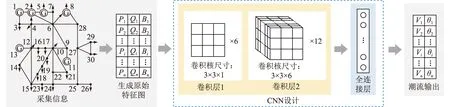
图3 CNN的设计示意Fig.3 Schematic diagram of design of CNN

4.1 卷积层

基于第3章的原始特征图，文中采用2个卷积层从原始特征图中进一步提取信息。每个卷积层由多个卷积核构成。对每一层而言，卷积核越多，其特征图越多，更多信息被挖掘，同时计算量也越大。对卷积层1，取尺寸为3×3×1×6的卷积核；对卷积层2，取3×3×6×12的卷积核。其中，卷积核4个参数分别为长、宽、深度与个数。此外，采用零填充以保证输入特征图的高度与宽度。

记Hk为CNN任一层的特征图，文中k取0，1，2，3。特殊地，当k取0时，H0为原始特征图，即第3章设计的特征图。对于每一层特征图，其上一层特征图经卷积运算后，采用非线性函数(称为激活函数)计算本层特征图。Hk的卷积运算如式(6)所示[18]。

Hk=h(Hk-1⊗Wk+bk)

(6)

式中：Wk为第k层卷积核的权值矩阵；⊗为卷积运算符；bk为第k层的偏置向量；h为激活函数。主流函数包括Sigmoid、tanh与ReLU等，考虑到ReLU函数在加速权值梯度下降收敛与计算量上的优势，文中取ReLU为激活函数，其定义如式(7)所示。

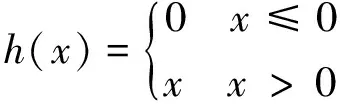
(7)

4.2 全连接层

全连接层本质为矩阵乘法，相当于特征图的空间变换，提取并整合多层卷积的计算结果。另一方面，全连接层可用于维度变换，尤其是对多层卷积后的高维数据降维，并保留其中有效信息。

全连接层按式(8)计算，上一层特征图经加权求和后，通过激活函数得到输出结果。

Hk=h(Hk-1wk+bk)

(8)

式中：wk为第k层权值向量；Hk为输出的潮流结果。此处，h仍取ReLU函数。

5 算例分析

文中基于Matlab仿真平台，在IEEE 30，IEEE 39，IEEE 57，IEEE 118四个标准系统中对比验证了文中方法的有效性，标准系统数据可参考MATPOWER手册[19]。为保证样本的随机性，采用蒙特卡洛法抽取N-2故障样本，以保证每个样本中有任意2条支路退出运行。此外，样本算例中负荷与发电机出力的随机性也通过蒙特卡洛抽样实现。其中，各负荷变化范围为标准工况的50%～150%，各机组出力变化范围为标准工况的80%～120%。

5.1 评估指标

5.1.1 精度评估指标

为便于直接与传统ANN的潮流结果对比，文中以AC算法的电压幅值与相角结果为基准值，使用算例集各节点电压与相角的平均误差评估开断潮流的分析精度。对于含N个样本的算例集，分别按式(9)与式(10)定义平均电压误差EV与相角误差Eθ，二者数值越小，潮流结果精度越高。

(9)

(10)

5.1.2 速度评估指标

(1) 计算时间。以秒为单位，考核方法的总计算时间T。T越小，潮流计算速度越快。

(2) 加速比。以AC算法的总计算时间TAC为参考，定义加速比R，如式(11)所示。R越大，潮流计算相对AC算法的速度优势越明显。

(11)

5.2 精度分析

5.2.1 训练样本占比的影响

训练样本占总样本的比例会影响CNN的强壮性，与测试集的平均误差直接相关。记N个算例中训练样本数为Ntrain，定义训练样本数占比σ为：

(12)

随机抽取IEEE 30节点系统10 000个N-2算例，设置不同σ分别训练CNN，统计训练集与测试集的潮流误差，如表1所示。

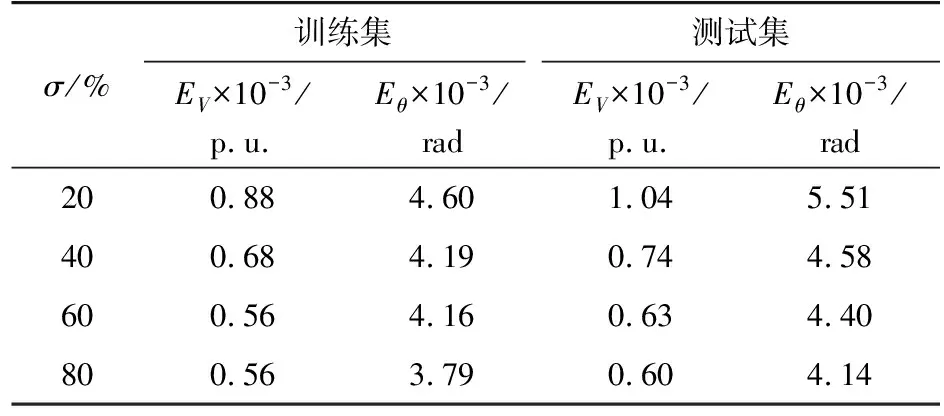
表1 不同σ下的潮流误差Table 1 Load flow error with different σ

随着σ上升，训练集与测试集中的EV与Eθ均不断减小，测试集与训练集的计算精度愈加相近。理论上，训练集数量趋于无限时，误差可接近0。然而，将所有N-2故障算例纳入训练集既不可行，也没有意义。考虑到表1中σ取60%与80%时，测试集与训练集的结果已非常接近，故余下仿真中σ取75%。

5.2.2 训练时长的影响

CNN的充分训练能够构建原始特征图到潮流结果的非线性映射，然而，单次训练基于线性方程求解，实际训练常以多次反复迭代的形式来拟合。一般而言，随着迭代次数增加，相应的训练时间延长，CNN的分析精度提高。当迭代次数增大到一定程度时，训练时长对CNN性能的提升效果反而下降，极端情况下甚至可能出现“过拟合”。以5.2.1节中开断计算场景为例，设置σ=75%，以IEEE 30节点系统为例，取迭代次数1～5 000(单次迭代的训练时间约3.8 s)训练CNN。训练时长对测试集分析精度的影响如表2所示。

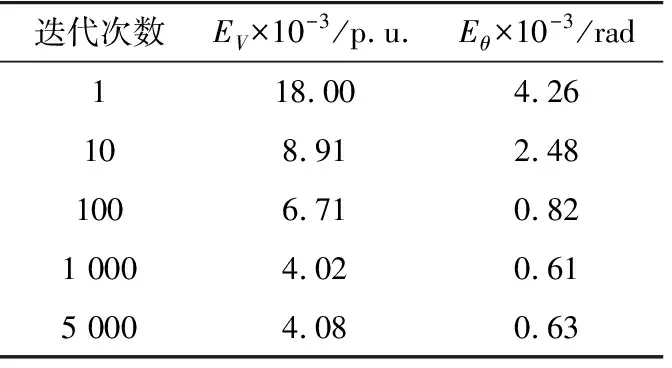
表2 不同训练时间下的潮流误差Table 2 Load flow error under different training time

由表2可见，随着迭代次数从1增加到100，测试集的相角与电压误差几乎降低80%；将迭代次数进一步增加到1 000，误差仅下降30%；继续增加迭代次数到5 000，误差反而略有增大，可能出现“过拟合”。为此，文中算例的训练过程统一采用500次迭代。

5.2.3 不同系统的影响

为校核文中方法在不同系统中的鲁棒性，在IEEE 30，IEEE 39，IEEE 57，IEEE 118节点系统中各取5 000个算例，以75%算例为训练集，余下为测试集。选择经典的ANN方法为比较对象，设置其网络宽度为10，深度为1，其输入信号、训练集、测试集均与文中CNN方法相同。

表3对比了CNN与ANN在不同系统中开断潮流的分析精度。相比ANN方法，文中设计的CNN分析框架使电压误差至少降低为原误差的三分之一，相角误差降低近1个数量级。且在不同系统中，文中方法将电压平均误差控制在0.01内，相角误差控制在0.03内，具有鲁棒性。

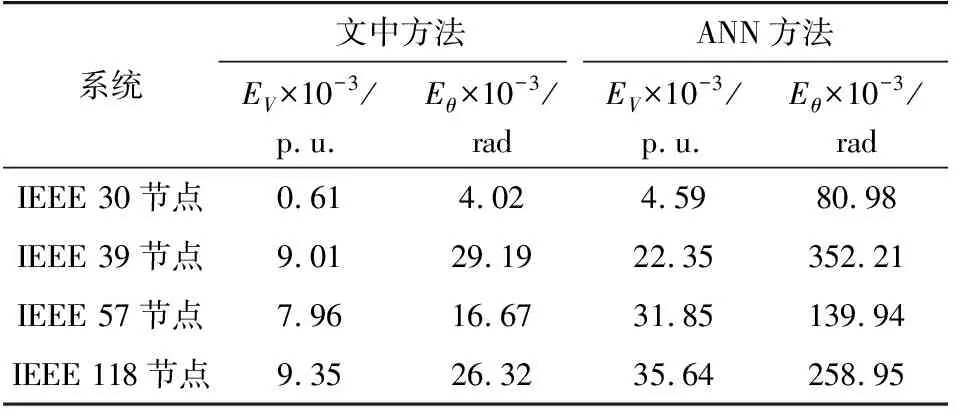
表3 不同系统中的潮流精度Table 3 Load flow accuracy in different systems

5.3 速度分析

表4对比了文中方法与AC算法在5.2.3节中测试集的计算速度。相比传统AC算法，文中方法将1 500个算例的计算时间控制在0.5 s以内，可满足实际系统的在线分析需求。相比传统AC算法，文中方法在4个典型系统中使速度提高约80倍，且加速比随系统规模增大而增大。因此，系统规模越大，文中方法的提速效果越明显。

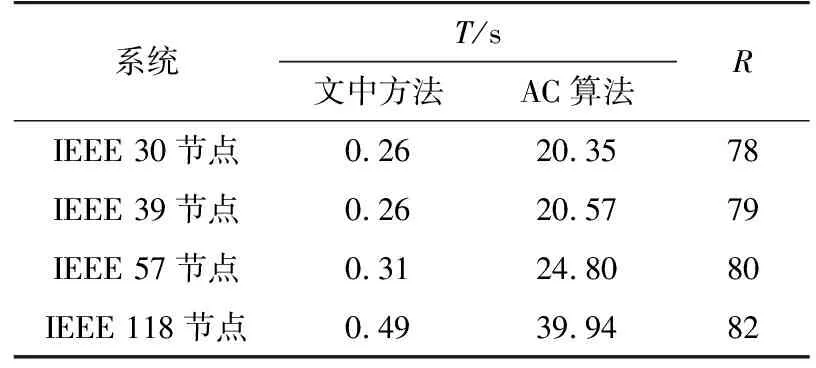
表4 不同系统中的潮流速度Table 4 Load flow speed in different systems

值得一提的是，AC算法在IEEE典型系统中的迭代一般不超过10次，而在实际大系统中的潮流迭代一般超过10次。随系统规模的扩大，AC算法计算量显著增长，文中方法的速度优势越显著。

6 结语

针对现有潮流计算方法难以实现N-2线路开断故障在线计算的问题，文中基于CNN提出了一种电力系统开断潮流的快速计算方法。文中方法以故障前后工况与拓扑的变化信息构建原始特征图，设计卷积神经网络建立原始特征图与故障后节点电压、相角的非线性的映射关系。相对经典的AC算法，CNN方法避免了复杂模型的反复迭代求解，使潮流计算速度提高约80倍。相比传统的ANN模型，CNN方法使电压与相角误差降低约1个数量级。另外，多个IEEE系统的仿真结果验证了CNN方法的强壮性。

AI方法引入电力系统静态安全分析已经二十余载，至今仍有一些问题亟待解决，包括训练集与测试集的数量问题；将潮流计算过程与静态安全评估、控制相结合，基于CNN进一步实现有功与无功潮流的计算；高阶故障开断潮流的快速可靠计算等。