浅孔留矿法与同步充填留矿法放矿过程力链演化特征比较
刘恩江 陈庆发 刘 军
(广西大学资源环境与材料学院,广西 南宁 530004)
在浅孔留矿法大量放矿阶段,若围岩暴露面积超过极限暴露面积,可能发生围岩片落与围岩大范围岩移现象,造成堵塞漏斗,甚至是地表沉陷[1]。为克服浅孔留矿法存在的不足,陈庆发教授于2010年提出了同步充填采矿技术思想,并同时提出了一种具有代表性的采矿方法——大量放矿同步充填无顶柱留矿采矿法[2](简称“同步充填留矿法”),是“协同开采”理念的具体实践。由于该方法在大量放矿前预先在留矿堆表面铺设柔性隔离层,使得放矿规律发生重大改变,突破了传统放矿理论的描述范围[3-5]。但同步充填留矿法与浅孔留矿法放矿过程中,采场内聚合体的性态介于固体和液体之间,表现出散体介质体系的性质。该体系中,矿石颗粒受自身重力、外部载荷等因素影响,使矿石颗粒之间相互挤压接触,形成诸多力的传递路径,称为力链[6]。在孙其诚[7-8]等提出的“(微观)颗粒—(细观)力链—(宏观)散体介质整体”多尺度结构研究框架中,细观层面的力链是连接单个颗粒与散体介质体系的桥梁,力链的复杂力学响应对散体介质体系宏观行为起到了决定性作用[9]。因此,开展浅孔留矿法与同步充填留矿法放矿过程散体介质力链演化特征的对比研究具有重要意义。
近年来,部分学者围绕力链受力特性与演化特征做了大量研究工作。在散粒体宏观形变方面,安令石[10]分析了路基土颗粒间力链演化规律及平均配位数的变化规律;宜晨虹等[11]采用离散元方法研究了不同数量点缺陷的二维颗粒体系在各向同性压缩和纯剪切试验时力链的几何分布特征。在散体介质力学行为方面,TORDESILLAS等[12]从力链演化和相关运动学的角度研究了应变局部化过程中非共轴性的微观力学起源;刘洋等[13]揭示了剪切过程中强力链在力学层面上承担与传递了相对较大的外载荷;陈凡秀等[14]阐述了力链网络在外荷载下的微细观统计效应对体系宏观力学性质的影响规律;徐正红[15]通过定义颗粒间的位移模式,根据热力学理论建立了力链压曲变形的能量方程。
基于两种采矿方法放矿过程中采场内聚合体均表现出散体介质性质的共性,本研究开展了同步充填留矿法与浅孔留矿法放矿过程中矿石散体内部力链演化特征的数值模拟研究,旨在通过力链演化特征的对比,了解同步充填留矿法与浅孔留矿法放矿过程中矿石散体细观力学变化规律的差异,进一步强化对同步充填留矿法放矿过程矿石流动规律的认知,为同步充填留矿法的放矿管理提供指导。
1 数值试验模型构建
1.1 接触模型确定
在本课题组先前进行的物理试验模型中,采用石子模拟矿石颗粒,并对相关物理力学参数进行了测定,在此直接引用,不再赘述[16]。实际放矿过程中,矿石散体是由大量体积、形态均不相同的块体组成。虽然PFC软件可以将体积、形态均不相同的块体粘结在一起,但是对每个块体体积、形态进行精确描述是无法实现的。即使采用随机形态块体对放矿散体进行模拟,在后期分析计算过程中也会频繁出现漏斗堵塞的现象,影响最终的统计结果。文献[17]建议通过调整滚动摩擦系数大小来模拟颗粒形态对散体介质体系流动的影响,且PFC2D5.0版本所提供的接触模型中,抗滚动线性接触模型相较于其他模型而言,增加了抗滚动系数,会降低颗粒的转动能力,与非均匀块体间的接触相近[18]。因此,本研究选取抗滚动线性接触模型模拟矿石颗粒之间的接触,以抵消矿石颗粒形态对矿石散体流动的影响。
由于抗滚动线性接触模型可抵消颗粒形态对矿石散体流动的影响。因此,本研究采用固定形态颗粒簇代表矿石颗粒,通过调整抗滚动摩擦系数大小,实现模拟矿石散体的目的,并根据石子粒度范围测定结果,选取占比最大的粒度范围(7~12 mm)作为数值试验模型中矿石颗粒半径的参考取值区间,即将矿石颗粒半径设置为8 mm。
1.2 放矿数值试验模型构建
(1)墙体生成。利用“wall creat”命令构建一个长168 cm、宽128 cm、放矿口间距为24 cm的单漏斗放矿数值试验模型。整个模型的边壁由23面墙组成,其中,底部由尺寸相同且标号从左到右依次为1~7号的放矿口组成,放矿口侧壁与水平面呈45°夹角,所有放矿口共计21面墙;剩余2面墙代表数值试验模型的边壁。
(2)初始颗粒生成。通过“ball generate”命令在墙体模型Y轴正方向0.08~128.00 cm范围内生成若干矿石颗粒,这些颗粒的重力加速度均为g=9.81 m/s2,其细观力学参数如表1所示。为使散体介质体系内的颗粒尽快充填密实,初始颗粒的接触模型设置为线性接触模型,颗粒之间的摩擦系数取0.3(多次调试综合取值);同时为方便观察放矿过程中矿石颗粒的流动现象,待模型平衡后,以10 cm间隔将矿石颗粒赋予不同的颜色,并删除Y轴正向128.00 cm以上的废石颗粒。

(3)计算颗粒生成。模型平衡后,将颗粒接触模型由线性接触模型变为抗滚动线性接触模型,此时散体介质体系内颗粒的细观力学计算参数如表2所示。在对浅孔留矿法进行模拟时,打开4号放矿口后,矿石颗粒从放矿口放出,矿石流动随即开始。在对同步充填留矿法进行模拟时,利用“Cubic”命令在矿石颗粒上方采用平行黏结方式生成一排长250 cm、半径为0.001 5 cm的颗粒,用以模拟柔性隔离层,隔离层细观力学参数如表3所示。同时,为实现同步充填效果的模拟,每次放矿结束后,在柔性隔离层上方生成适量的充填废石颗粒(其细观力学参数取值与计算过程中矿石颗粒细观力学参数相同),待模型在自重作用下解算平衡后,删除多余的充填颗粒。

通过以上步骤建立的留矿法放矿数值试验模型如图1所示。

2 力链演化特征研究
力链的形成需满足3个条件[19-21]:①颗粒串内相互接触颗粒之间的接触应为强接触,即颗粒之间的接触力应大于等于散体介质体系内的平均接触力;②必须由3个及3个以上相互接触颗粒所组成的颗粒串;③颗粒串内相邻接触之间的夹角应小于某个角度值α(α由模型内颗粒的平均配位数决定)。
根据上述力链形成条件,设置力链识别判据,编写力链识别程序,实现力链的自动检索及识别,为力链演化特征研究做准备。力链自动检索及识别的具体流程为:①利用PFC2D导出不同放矿节点条件下散体介质体系内部颗粒位置、半径及接触位置、接触力大小等信息;②为满足条件①要求,筛选出体系中大于平均接触力的接触;③依据条件②、条件③,利用Matlab软件编制力链识别程序,实现对力链的检索及识别。
2.1 力链数量及长度变化分析
利用力链形成条件编制力链识别程序,根据PFC2D输出不同放矿节点条件下散体介质体系内部接触力信息,对两种采矿方法放矿过程中不同放矿节点条件下散体介质体系内部的力链数量进行了统计,结果如图2所示。

由图2可知:浅孔留矿法放矿前中期,力链数量随着放矿次数增加而减少;而在放矿后期,随着放出矿石颗粒逐渐减少,力链数量维持在290条左右。但总体上看,整个放矿过程中力链数量仍随着放矿次数增加呈指数形式减少。同步充填留矿法放矿过程中,虽力链数量也随放矿次数增加而减少,但在放矿后期力链数量稳定在810条左右;相较于浅孔留矿法,同步充填留矿法放矿过程中力链数目不仅较多,而且波动幅度较小。
根据力链形成所需具备的3个条件可知,即便是强接触,也并非能够全部参与力链的组成。因此,对两种采矿方法放矿过程中强接触数量与力链接触数量占接触总数的比例进行了统计,结果如图3所示。

由图3可知:浅孔留矿法放矿过程中,强接触占接触总数的比例较小,始终保持在34%左右,上下波动幅度不超过1%;力链接触占接触总数的比例在放矿初期保持在13%左右,至放矿后期开始,逐渐增加至16%左右。同步充填留矿法中,随着放矿次数增加,强接触占比逐渐由37%减小至32%,并在放矿后期逐渐保持稳定;力链接触占比整个放矿过程均稳定在17%左右,上下波动幅度不超过2%。
综合图2和图3可知:浅孔留矿法放矿前中期,随着矿石颗粒逐渐放出,体系内部接触总数也在不断减少,由于强接触占比与力链接触占比均保持相对稳定,使得力链总数出现了减少现象;在放矿后期,矿石颗粒逐渐减少,体系内部接触总数也逐渐减少,虽强接触占比仍保持相对稳定,但力链接触占比逐渐增加,使得力链总数保持在一种相对不变的状态。对于同步充填留矿法而言,放矿前中期,矿石颗粒逐渐减少,体系内部接触总数及强接触占比也在不断减少,但力链接触始终保持相对稳定,使得体系内部力链数量逐渐减少;放矿后期,矿石颗粒逐渐减少,在柔性隔离层及上覆充填废石自重的影响下,体系内部载荷逐渐稳定,强接触及力链接触也逐渐趋于稳定,使得力链数量也逐渐趋于稳定。
基于对力链数量及强接触、力链接触占比的研究,将不同放矿节点条件下散体介质体系内部力链数目进行归一化处理,进一步对两种采矿方法放矿过程中不同放矿节点条件下体系内部的力链长度分布概率进行了统计,结果如图4所示。

由图4可知:同步充填留矿法与浅孔留矿法放矿过程中,不同放矿节点条件下力链长度的分布概率均表现出相似的变化规律,即力链长度越长,其形成的概率越小,两者呈指数关系递减。需要注意的是,力链长度存在大于15的情况;但在力链长度统计过程中,长度大于15的力链数量极少,并不会对其变化规律产生影响。因此,本研究在统计时未将力链长度大于15的力链统计在内。拟合公式采用指数函数公式:

式中,A为计算系数。
利用式(1)对不同放矿节点条件下力链长度概率分布进行拟合时,拟合度均达到0.99以上,拟合效果极好。对比发现,本研究得到的不同放矿节点条件下力链长度概率分布规律与已有研究[22-23]得到的结论相符。
根据图4中力链长度概率分布规律,将长度(L)等于3的力链视为短力链,长度为4~6的力链视为中等长度力链,长度大于6的力链视为长力链。统计了两种采矿方法放矿过程中不同放矿节点条件下3种力链的概率分布,结果如图5所示。
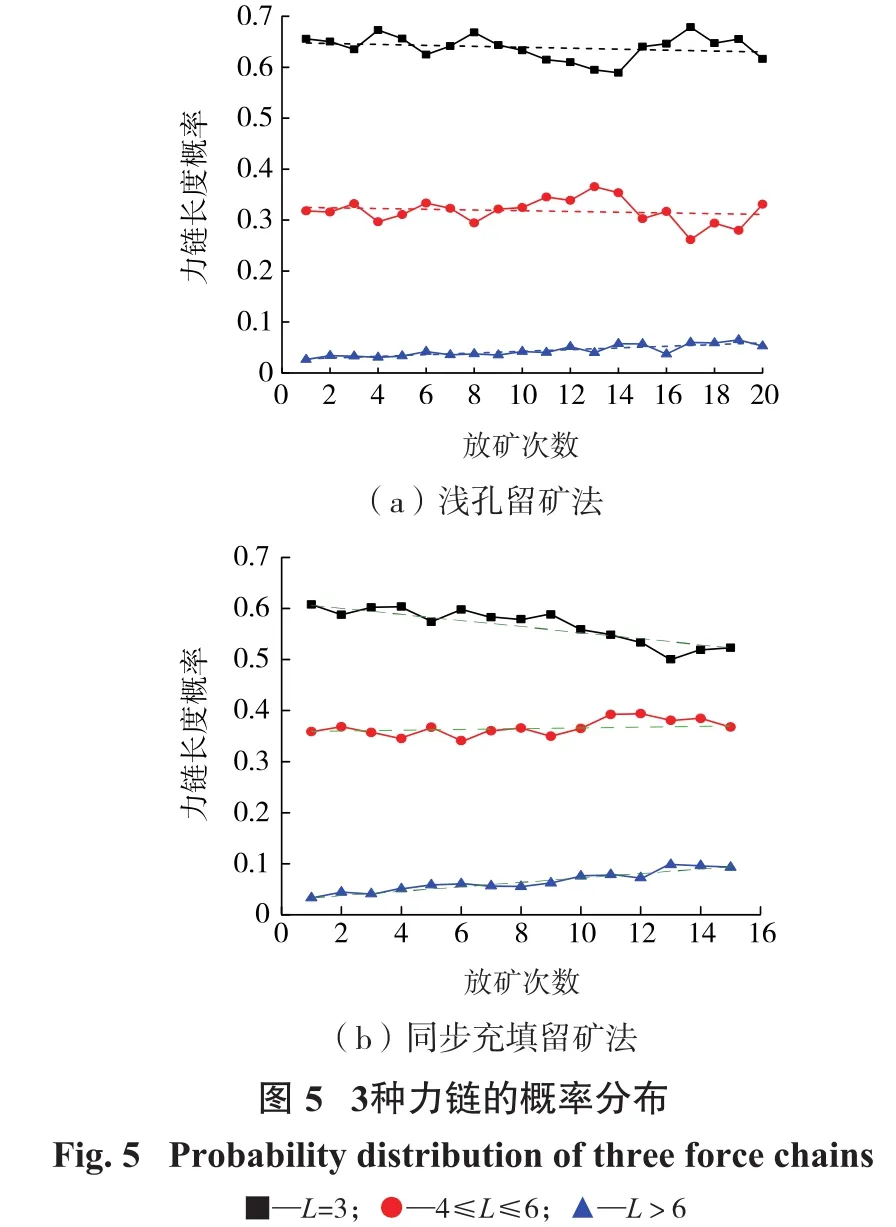
由图5可知:浅孔留矿法放矿过程中,短力链约占全部力链数目的65%,中等长度力链约占全部力链数目的32%,且短力链和中等长度力链呈现出相反的变化规律——短力链占比增加时,中等长度力链占比就会减少;长力链占比在放矿初期保持在2%左右,放矿过程结束时,逐渐增加到7%左右。这是由于放矿初期,矿石颗粒流动打破了体系的原始应力,体系内部不断发生力链“断裂—重组”过程,导致原本稳定的力链网络遭到破坏,使得放矿初期3种力链比例保持相对不变;随着放矿的进行,虽然体系内部仍在发生着力链“断裂—重组”过程,但矿石颗粒放出量逐渐减少,体系逐渐趋于稳定,荷载逐渐被长力链分担,新的力链分布网络逐渐形成,使得放矿后期长力链数目逐渐增多。
对于同步充填留矿法,虽然矿石颗粒流动也打破了体系的原始应力,体系内部也不断发生力链“断裂—重组”过程,破坏了原本稳定的力链网络,但在充填废石荷载的作用下,长力链的形成概率会增加。因此,短力链占比由61%逐渐降至50%左右,中等长度力链占比始终保持在37%左右,长力链占比则由放矿初期的3%左右逐渐增加到10%左右。
但由图5也可看出:两种采矿方法放矿过程中3种力链占比虽有不同,但3种力链整体分布规律是一致的,即短力链仍是整个力链网络的主要组成部分,中等长度力链次之,长力链占比最少。
2.2 力链强度演变过程分析
某条力链中所有接触力的均值为该力链的力链强度,反映了散体体系的承载能力,其表达式为

式中,F为力链强度;N为该力链中接触的数量;fi为该力链中接触编号为i的接触力。
两种采矿方法放矿过程中,不同放矿节点条件下力链强度的演变规律如图6所示。

由图6可知:浅孔留矿法放矿过程中,力链强度波动幅度较大,总体上随着放矿次数增加呈指数形式减小。这是因为在放矿过程中,随着矿石颗粒被逐渐放出,散体介质体系内部矿石颗粒逐渐减少,体系内相互挤压的矿石颗粒减少,导致力链强度逐渐减小。同步充填留矿法中,受上覆充填废石颗粒自重影响,力链强度在放矿前期基本保持不变,放矿中期力链强度出现缓慢下降,放矿后期力链强度又逐步上升,总体波动幅度较小。这种力链强度无较大差别的变化规律也表明散体介质体系整体并无太大变化。根据不同放矿节点条件下散体介质体系内部力链强度的变化规律,对两种采矿方法放矿过程中体系内部的力链强度概率分布进行了统计,结果如图7所示。

由图7可知:两种采矿方法放矿过程中,不同放矿节点条件下力链强度的概率分布规律具有相似性,即力链强度的概率分布均先呈指数形式上升,并分别在0.65、0.7(为平均接触力)处达到峰值后,再呈指数形式下降。同时,不同放矿节点条件下相似的力链强度概率分布规律也表明,散体介质体系内部力链网络大部分由弱力链组成,强力链只占力链网络的小部分,强弱力链的相互交织构成一个完整力链网络,共同维持着整个散体介质体系的稳定。
对不同放矿节点条件下散体介质体系内部力链强度分布概率进行了拟合,拟合函数为

式中,A、B、C、D为计算系数。
用式(3)对力链强度分布进行拟合后发现,拟合程度极好,拟合度均达到0.999以上。
2.3 力链方向分布变化分析
识别出一条力链后,在PFC2D输出的信息中调用出该力链中所有相邻颗粒之间的接触夹角信息,取该力链中所有接触夹角的平均值,便可以确定该力链的方向。为了解两种采矿方法放矿过程中散体介质体系内部力链方向分布的变化规律,将360°等分为36个区间,并对每个区间内的力链数量及强度进行统计,求出每个区间内力链的平均强度,绘制了不同放矿节点条件下力链方向分布图,如图8所示(仅选择各自具有代表性的力链方向)。
为定量描述散体介质体系内部力链方向的变化规律,结合前人研究成果[24],对散体介质体系内部力链强度与方向的统计结果进行拟合,拟合公式为

式中,fn(θ)为力链强度的分布函数;f0为力链平均强度;ωn为傅里叶级数,其值大小表示力链方向分布的各向异性程度;θn为力链的主方向。
用式(4)对浅孔留矿法放矿过程中不同放矿节点条件下的力链强度及方向进行拟合后发现,该式对前7次放矿过程中力链方向的拟合效果较好;自第8次放矿开始至整个放矿过程结束,散体介质体系内部力链强度及方向的分布关系发生了较大变化,不再满足该式表达的数值关系。
由图8(a)可知:自第8次放矿开始直至第14放矿结束,力链方向分布呈现出6个较为明显的波峰,最小正周期为60°。定义自第8次放矿开始至第14次放矿结束的过程中,力链方向分布拟合的三角函数公式为
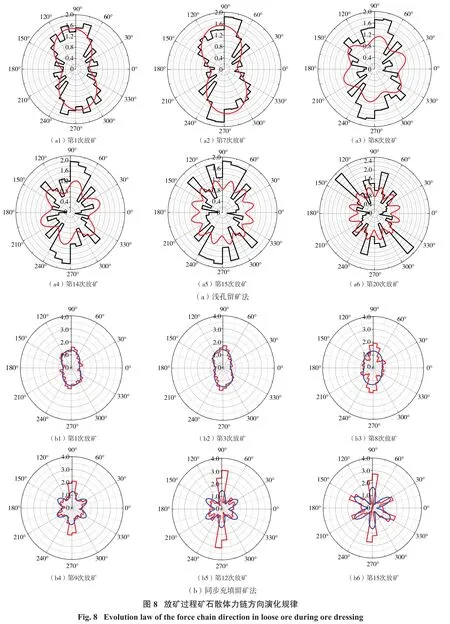

自第15次放矿开始直至整个放矿过程结束,力链方向分布呈现出较多明显的波峰,最小正周期为30°。定义自第15次放矿开始至整个放矿结束的过程中,力链方向分布拟合的三角函数公式为

同样地,利用式(4)对同步充填留矿法放矿过程中不同放矿节点条件下的力链强度及方向进行拟合后发现,该式仅对前8次放矿过程力链方向的拟合效果较好,而第9次及以后的放矿节点,该式表达的数值关系不再满足体系内部力链强度及方向的分布关系。通过对比发现,第9次及以后的放矿节点,力链方向分布也呈现出6个较为明显的波峰,最小正周期也为60°。因此,本研究利用式(5)对同步充填留矿法第9次及以后放矿过程中的力链方向分布进行拟合。
通过对力链方向进行拟合发现,式(4)至式(6)均能对对应放矿节点力链方向波峰进行较好地反映,总体拟合效果较好。两种采矿方法不同放矿节点条件下的参数拟合结果如表4、表5所示。


综合图8(a)及表4可知:浅孔留矿法放矿过程中力链方向分布的变化规律可以分为3个阶段:
(1)第1个阶段为第1次放矿开始至第7次放矿结束。该阶段内散体介质体系内部力链方向呈现出相似的变化规律,力链主方向均为沿铅垂方向。这是由于在本阶段内矿石颗粒放出较少,由矿岩颗粒组成的散体介质体系内部处于相对固结的状态,使得散体介质体系内部力链分布的主方向θn保持在90°左右,力链方向分布形态近似花生状。对于本阶段内力链分布各向异性程度表征参数ωn,受颗粒自身重力及放矿口等效荷载的影响,ωn基本保持不变。
(2)第2阶段为第8次放矿开始至第14次放矿结束。该阶段内散体介质体系内部力链方向也呈现出相似的变化规律,但与前7次放矿过程中力链方向的变化规律有所不同。由于在本阶段内,体系内部松动范围内的矿石颗粒呈漏斗状下落,向漏斗口上方的放出体内部滑动,并随着颗粒不断放出,体系内部松动范围占整个散体介质体系的比例逐渐增加,使得力链方向的分布形态由花生状演变为花瓣状,力链主方向也由铅垂方向演变为沿铅垂方向及与水平方向呈±45°夹角方向。对于本阶段内力链分布各向异性程度表征参数ωn,受降落漏斗及流动颗粒的影响,力链分布各向异性程度表征参数ωn逐渐增大。
(3)第3阶段为第15次放矿开始直至整个放矿过程结束。此阶段内散体介质体系内部力链方向也呈现出相似的变化规律,但与前两个阶段力链方向变化规律不同,力链主方向分布由3个演变为4个(由铅垂方向、与水平方向呈±45°夹角方向演变为与水平方向呈±45°夹角、±75°夹角方向)。究其原因,是因为在本阶段,矿石颗粒放出量逐渐减少,并在散体介质体系表面形成自由面,颗粒自重及自由面的共同作用影响了本阶段散体介质体系内部力链方向的分布。本阶段内力链分布各向异性程度表征参数ωn也相应增加。
对于同步充填留矿法,结合图8(b)及表5可知,前8次放矿过程中散体介质体系内力链方向分布的变化规律具有一致性,后7次放矿过程中力链方向分布变化规律具有一致性。因此,同步充填留矿法放矿过程中力链方向分布的变化规律可以分为2个阶段:
(1)第1个阶段为第1次放矿开始至第8次放矿结束。该阶段内散体介质体系处于初始固结状态,系统自身重力是影响力链方向分布的主要因素,使得力链主要沿铅垂方向分布,故散体介质体系内力链分布主方向θn在90°左右,力链方向分布形态也近似花生状。该阶段体系内颗粒主要受自身重力及放矿口等效荷载的影响,而这两种荷载在放矿过程中为一定值,所以各向异性程度ωn基本保持不变。
(2)第2阶段为第9次放矿开始至第15次放矿结束。该阶段内,随着矿石颗粒持续放出,受充填废石上覆荷载及隔离层形状的影响,体系内部力链方向分布形态由花生状逐渐变为花瓣状,力链分布主方向也由1个演变为3个(铅垂及与水平方向呈±30°夹角的方向)。基于前文对力链数量、力链强度的研究,结合力链方向的变化可知,同步充填留矿法可在一定程度上控制围岩的稳定性。对于力链分布各向异性程度表征参数ωn而言,第8次放矿之后,隔离层上覆荷载对力链方向分布的影响越来越大,且随着充填废石的增加,上覆荷载逐渐增大,所以体系内力链各向异性程度ωn逐渐增大。
对于两种采矿方法放矿过程中矿石散体内部力链平均强度f0而言,由于其经过归一化处理,所以其一直保持在1.00。
3 结 论
基于放矿过程中采场内聚合体均表现出散体介质性质的共性,借助数值模拟手段,开展了同步充填留矿法与浅孔留矿法放矿过程中矿石散体内部力链演化特征的数值模拟研究,主要得到以下结论:
(1)同步充填留矿法放矿过程中,矿石散体内部强接触占比随放矿次数的增加逐渐由37%减小到32%,并在放矿后期逐渐保持稳定,而力链接触在放矿过程稳定在17%左右(上下波动幅度不超过2%);浅孔留矿法放矿过程中,矿石散体内部强接触占比始终保持在34%左右,上下波动幅度不超过1%,力链接触占接触总数的比例在放矿初期保持在13%左右,至放矿后期开始,逐渐增加到16%左右。
(2)两种采矿方法放矿过程中,矿石散体内部力链数量随着放矿次数增加呈现出不同的变化规律。但不同放矿节点条件下,短力链仍是整个力链体系的主要组成部分,中等长度力链次之,长力链占比最少;且力链长度的概率分布规律也高度一致,均呈指数形式减少。
(3)相较于浅孔留矿法,同步充填留矿法放矿过程中矿石散体内部力链强度波动幅度较小,但两种采矿方法放矿过程中,不同放矿节点条件下力链强度的概率分布规律高度相似,均先呈指数形式上升再呈指数形式下降。
(4)浅孔留矿法放矿过程中,力链方向由放矿初期的单一铅锤方向逐渐演变为3个,并在放矿后期逐渐由3个演变为6个,呈现出明显的阶段性变化规律;同步充填留矿法放矿过程中,力链方向仅由放矿初期的单一铅锤方向逐渐演变为3个,也呈现出明显的阶段性变化规律。对于力链方向分布各向异性程度表征参数ωn而言,两种采矿方法各阶段内均呈现出不尽相同的变化规律。

