一种基于遗传模拟退火算法的通信卫星资源规划方法
王 涛,喻 韬
(北京跟踪与通信技术研究所,北京 100094)
0 引言
20世纪60年代以来,卫星通信技术迅猛发展,在各领域都得到了广泛发展,卫星通信已成为天地通信、无线信息通信的最重要手段。近年来,随着卫星通信技术的不断发展,在轨通信卫星的数量和种类均得到不断增加,可供各个行业使用的通信卫星资源也日益丰富。因此,如何有效地挖掘通信卫星资源使用潜力,实现卫星资源规划的不断优化,最大限度地满足各类资源需求是目前卫星通信系统资源管理急需解决的关键问题[1-6]。
通过抽象分析,可将通信卫星资源的统一规划调度视为一种在有限的频域和时域资源内寻找多个针对不同用户需求的通信任务的组合优化问题。文献[7-9]开展了基于遗传算法的资源动态调度研究;文献[10]提出了一种基于遗传算法的通信卫星资源动态调度方法,并开展了实验验证;文献[11]提出了在栅格化信息网环境下的卫星接入资源调度优化问题,提出了一种基于贪婪算法(GA)的调度方法,并给出实验算例对算法进行了分析验证;文献[12-13]分别基于粒子群优化算法对云计算资源调度问题和卫星地面站资源调度问题开展了相应的策略设计和方法研究。本文在上述研究基础上,提出了一种基于遗传模拟退火算法的资源规划方法,旨在实现通信卫星资源规划的进一步优化,增强卫星资源管理能力,提高资源规划效率和资源利用效能。
1 通信卫星资源规划问题模型
通信卫星的资源统一规划是利用有限的可用通信卫星资源,根据各个通信任务不同的执行时间需求和频率带宽需求,对各个任务进行时间资源和频率资源进行匹配排列的过程,不同的匹配排列结果可能会导致不同的资源利用率。通信卫星资源统一规划的目标在于如何通过优化的算法进行任务排列,在完成卫星通信任务保障的同时最大限度地争取通信卫星资源的高效利用。
面向多任务的资源统一规划可以采用如图1所示的二维坐标系表征。

图1 通信任务二维坐标系排列Fig.1 2D coordinate system arrangement of communication tasks
通信卫星资源可分为时间和频率2个维度,假设卫星通信任务数量为n,其中第i(1≤i≤n)个任务的起止时间分别为Si和Ei,时间范围为T1~T2(T1≤min(S1,S2,…,Sn)≤max(E1,E2,…,En)≤T2),可用频率范围为F1~F2,其在二维坐标系中形成的图形面积记为A,n个任务排列完成后可排入二维区域内的任务块的面积之和记为A0。对于n个通信任务的资源统一规划问题,则可以抽象为如何找到一种n个任务的排列方式使得A0/A值最大的问题。
2 遗传模拟退火算法的基本思想
遗传算法[14-15]作为一种智能优化算法,通过特定的编码方式,建立原问题的解空间和特定的编码空间之间的映射关系,使用选择操作、交叉操作和变异操作对种群内所有个体进行选择,择优产生新个体,重复进行此过程,直到达到算法设定的收敛条件后结束。通过对该编码空间的不断搜索,作为对原问题解空间搜索的替代,可以实现原问题的寻优和求解。遗传算法模仿自然界生物遗传寻优的思想解决最优解问题,其全局搜索能力较强,但局部搜索能力较弱,导致算法的收敛速度较慢。
模拟退火优化算法[16-17]最初来源于对固体退火过程的思考与模拟。模拟退火算法可用来解决多种组合优化问题,其内能E可理解为目标函数f,温度T可视为控制参数t。由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解。退火过程由冷却进度表控制,包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。模拟退火算法局部搜索能力强,具备跳出局部最优解的能力,能够向全局最优解快速收敛。
综上分析,本文通过将遗传算法和模拟退火算法相结合,将遗传算法的全局搜索能力和模拟退火算法的局部搜索能力进行互补,提出了一种混合的改进算法,并基于该算法思想完成通信卫星资源规划的方法设计。
3 基于遗传模拟退火算法的资源规划方法
3.1 染色体编码
本文将每一个可能的资源分配方案都编码为一个染色体,考虑本文解决的是任务排序问题,常规的二进制编码不适用,采用十进制的编码方式,每一个染色体有n个基因,n表示任务的个数,任务的资源需求包括带宽、开始时间和结束时间等属性;卫星资源包括频段、起始频率和结束频率等属性,基于任务属性和卫星资源属性进行编码设计,将任务按照1,2,...,n进行编号,整个染色体表示每个任务的资源分配顺序,在进行分配时按照频率从低到高的规则依次寻找最先满足任务资源需求的资源池空间,并根据适应度函数进行计算。
3.2 适应度函数设计
适应度函数主要依据资源利用率最高原则进行设计,计算过程如下:
首先设计一个任务集合X={Wx,TSx,TEx,FSx,FEx},用于表征完成排列的个体,其中Wx表示任务x的带宽,TSx表示任务x的实际开始时间,TEx表示任务x的实际结束时间,FSx表示任务x的实际起始频率,FEx表示任务x的实际终止频率。对于每一个个体SEQi,按照其任务序列的顺序依次取出相应的通信任务,对于每一个任务t,根据实际应用可假设其可接受的最早开始时间为t0,可接受的最晚结束时间为t1,任务持续时长固定为d,任务需要的频率带宽为w,进行如下排列:
① 首先在t0~t0+d的时间段内,从起始频率f0开始,查看f0~f0+w是否空闲,如果不空闲,则加一个频率偏移量Δf,继续查看f0+Δf~f0+Δf+w是否空闲,直至f0+Δf+w超出了终止频率f1。如果可以找到空闲频率,则将该任务块排列在t0~t0+d时间段内的相应频率位置上,将该任务放入集合X,否则继续下一步。
② 将起始时间加一个偏移量Δt,此时搜索的时间段范围为t0+Δt~t0+Δt+d,在该时间段内重复步骤①的搜索过程。如果可以找到空闲资源,则将任务块排列在t0+Δt~t0+Δt+d时间段内的相应频率位置上,将该任务放入集合X,否则继续增加偏移量Δt,直至t0+Δt+d﹥t1。如果此时仍未找到可用的频率资源,则将该任务标记为不可分配任务。
③ 将个体SEQi中所有任务依次排列完成后,计算其资源利用率f,即适应度函数:
3.3 遗传进化设计
3.3.1 种群初始化
初始种群的产生时,对每个任务随机生成一个优先级,按照优先级的次序分配,以形成一个个体。优先级生成公式如下:
Priority=WightArea×Area+WeightRatio×(L/W),
式中,WightArea是面积的权重,为随机产生的一个[0,1]的数;WightArea+WeightRatio=1,Area是带宽和时间的乘积,其中带宽单位为MHz,时间单位为天;L/W是时间与带宽的比值。
循环m次,生成规模为m的初始种群{SEQ1,SEQ2,…,SEQm}。种群初始化示意如图2所示。

图2 种群初始化示意Fig.2 Schematic diagram of population initialization
3.3.2 选择退火操作
对于规模为m的初始种群G,将种群中的m个个体依次进行适应度评价。原则上说,个体适应度值越大,该个体被遗传到下一代的概率也越大。
选择退火操作流程如图3所示。

图3 选择退火操作流程Fig.3 Flowchart for selecting annealing operation
为了避免遗传算法的“早熟”现象,使算法过早陷入局部最优解,本文不选择传统的轮盘赌、锦标赛等选择方法,而是引入模拟退火的思想,对选择的退火操作过程设计如下:
(1)随机选择初始群体G两个个体pi,pj,计算个体适应度值f(pi)和f(pj);
(2)采用模拟退火算法中的概率思想选择pi,pj其中之一遗传到下一代,即:
① 如果f(pi) ② 如果f(pi)≥f(pj),则以概率P选择pj遗传到下一代,其中, (3)重复(1)、(2),直到新一代群体中也包含m个个体。 3.3.3 交叉退火操作 交叉运算是遗传算法产生新个体的重要手段,通过让2个父代个体以某一交叉概率产生新一代的个体,该方式主要用于保持种群的多样性,但同时也导致进化后期收敛速度慢的问题,因此,在交叉运算中考虑引入模拟退火算法,其操作流程如图4所示。 图4 交叉退火操作流程Fig.4 Flowchart for cross annealing operation (1)选择父代中的一个个体pi,记为当前个体S。 (2)随机选择一个非pi的父代个体pj,将pi,pj以概率Pc进行交叉操作,形成新个体pn,记为S′,Pc可取值为0.7,交叉运算示意如图5所示。 图5 交叉运算示意Fig.5 Schematic diagram of cross operation 根据图5,选择交叉点,保留pi中交叉点之前的序列(1,3,6,4),然后将pj中的相应任务删除,留下的序列(5,8,7,2)拼接到pi的交叉点之后,形成新的个体pn。 (3)分别计算个体S和S′的个体适应值,记作f(S)和f(S′)。 (4)采用模拟退火算法进化,设循环次数为k,循环次数阈值为L,则: ① 如果f(S) ② 如果f(S)≥f(S′),则以概率P设定S=pn,其中, (5)循环(2)~(4),完成对父代中一个个体的交叉运算。 (6)循环(1)~(5),完成对所有父代个体的交叉操作。 3.3.4变异退火操作 变异运算是遗传算法产生新个体重要的手段,通过变异的方式将父代的一个个体变化为一个新个体。同交叉操作一样,变异操作在一定程度上影响了进化后期的收敛速度,因此在变异操作中同样引入模拟退火算法思想,变异退火操作流程如图6所示。 图6 变异退火操作流程Fig.6 Flowchart of variant annealing operation (1)选择父代中的一个个体pi,记为当前个体S。 (2)以概率Pm对pi进行变异操作,形成新个体pn,记为S′,Pm可取值0.1,变异运算示意如图7所示。 图7 变异运算示意Fig.7 Schematic diagram of mutation operation (3)分别计算个体S和S′的个体适应值,记作f(S)和f(S′)。 (4)采用模拟退火算法进行进化,设循环次数为k,循环次数阈值为L,则: ① 如果f(S) ② 如果f(S)≥f(S′),则以概率P设定S=pn,其中, (5)循环(2)~(4),完成对父代中一个个体的变异运算。 (6)循环(1)~(5),完成对所有父代个体的变异操作。 基于遗传模拟退火算法的资源规划流程如图8所示。 图8 基于遗传模拟退火算法的资源规划流程Fig.8 Flowchart of resource planning based on genetic simulated annealing algorithm (1)创建规模为m的初始种群; (2)对初始种群进行选择退火操作; (3)对选择退火后形成的种群进行交叉退火操作; (4)对交叉退火后形成的种群进行变异退火操作; (5)生成新的种群,并判断是否满足循环终止条件,一般终止条件为达到迭代次数、最优解多次迭代无明显变化或者最优解达到预期目标;如不满足则将新的种群作为下一轮迭代的初始种群,循环(2)~(5); (6)循环结束后,取出此时种群中适应度值表现最优的个体,作为问题的最优解。 本文对基于遗传模拟退火算法的资源规划方法进行了模拟仿真,并与传统的基于遗传算法的资源规划方法进行对比。对比测试分别在资源利用率和规划执行效率2个方面展开。 分别随机生成10,20,30,40,50,60,70,80,90,100个通信任务,依次对2种资源规划方式进行仿真,其资源利用率对比结果如图9所示。 图9 2种规划方式下资源利用率对比曲线Fig.9 Comparison curve of resource utilization under two planning modes 由图9可以看出,基于遗传模拟退火算法的资源规划方法的资源利用率整体要略高于传统的基于遗传算法的资源规划方法。 分别随机生成10,20,30,40,50,60,70,80,90,100个通信任务,依次对2种资源规划方式分别仿真,其规划任务完成时间对比结果如图10所示。 图10 2种规划方式下规划执行效率对比曲线Fig.10 Comparison curve of planning execution efficiency under two planning modes 由图10可以看出,基于遗传模拟退火算法的资源规划方法的规划执行率整体要优于传统的基于遗传算法的资源规划方法,算法性能更优。 本文通过对通信卫星资源统一规划问题进行建模,并分析了遗传算法和模拟退火算法的算法特性,提出了一种基于遗传模拟退火算法的资源规划方法,该方法能够有效提高通信卫星资源规划效率,并在一定程度上提升资源利用率,为通信卫星资源管理科学化、智能化水平的进一步发展探索了新的技术道路。
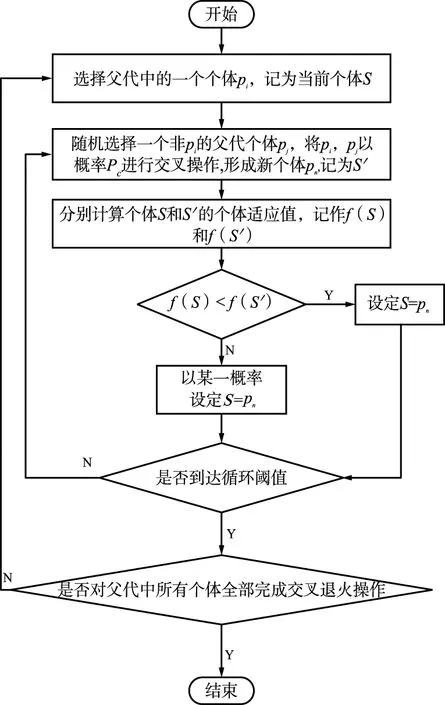



3.4 算法流程

4 实验结果与分析
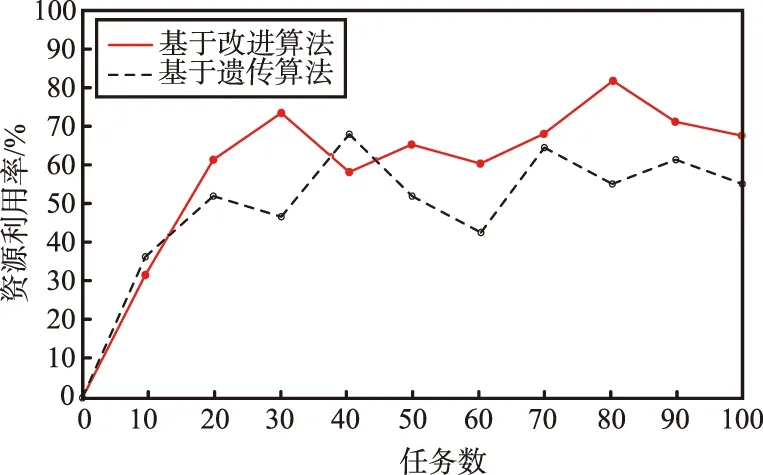
4.1 资源利用率对比
4.2 规划执行效率对比

5 结束语
——基于人力资本传递机制
——基于反向社会化理论的实证研究
——基于子女数量基本确定的情形

