中学生数学品格与价值观的问卷设计
喻 平,董林伟,郭庆松
中学生数学品格与价值观的问卷设计
喻 平1,董林伟2,郭庆松3
(1.南京师范大学数学科学学院,江苏 南京 210046;2.江苏省教育科学规划办公室,江苏 南京 210013;3.江苏省中小学教学研究室,江苏 南京 210013)
依据相关理论,编制中学生数学品格与价值观问卷.问卷包括4个一级指标:数学价值观念、数学思维品格、数学学习态度、学会数学学习,分别组成4个子量表.各子量表的二级指标分别是,子量表1:科学与文化价值、育人价值;子量表2:理性思维、探究思维;子量表3:乐于学习、主动学习、坚毅执着;子量表4:合作交流、善于学习.问卷有较好的结构效度和信度.
中学生;数学核心素养;问卷;测量
必备品格、正确价值观和关键能力是核心素养的3个基本要素,这3个要素既是教学目标设定的依据,也是学生数学学业质量评价的准绳.因此,基于核心素养的课程改革设计与实施,必须研究核心素养的评价问题,即如何考量学生的能力、品格与价值观的习得与发展水平,这是不完全等同于传统意义上对学生知识记忆、理解、掌握、运用的测量来评价学生学业质量的方法,无论是过程性评价还是终结性评价,都应当寻找新的理路或模型.
应该思考两个问题.第一个问题:如何评价关键能力.要走出只重知识考查的围栏,研究如何从“教知识考知识”转向“教知识考知识加能力”,后者与前者的评价基本形态可能相同,即采用传统的基本考试模式,主要是终结性评价,但是,考试的内容则应大相径庭,前者以知识为重,后者以能力为重.要研究的问题是,什么样的题目能够考查能力水平而非单纯地考查知识理解.这个研究也许涉及到要探讨通过知识学习如何转化为能力发展的心理机制的本源性问题.第二个问题:如何评价品格与价值观.从心理学角度看,必备品格与正确价值观属于非认知因素范畴,显然不能通过答题考试的方法来评价,它不宜采用终结性评价而应当是过程性评价形式.要研究的问题:评价学生的品格与价值观的形式和内容.这里聚焦于第二个问题.
1 问题提出
要研究品格与价值观的评价,无论是采用测量学方式还是采用观察学生行为变化的过程式评价,都需要事先建构一个指标体系.布卢姆(Bloom)将教学活动的目标分为3个方面:认知领域、情意领域和动作技能领域,每个领域都建立了指标.威尔逊(Wilson)根据布卢姆的理论结合对数学学科的深入分析,建立了数学学习的目标分类.这一模型在认知和情感领域对数学学习行为作了分类[1].其中情感领域包括:E兴趣和态度.E1态度.对待学习数学的态度,包括对数学学科重要性的认识.E2兴趣.对待数学学习的情感指向与热衷的态度.E3动机.对待数学学习的个体的内驱力.E4自我概念.学习者自称对待与数学学习活动关系方面的想法.威尔逊认为,在情感领域,根据评价目标进行测试是比较困难的,通常采用对学生的数学学习活动进行观察,或通过交谈和问卷调查并将其量化来获取数据.
将核心素养转化为具体的学习结果,并在此基础上开发出相应的测量工具,是国外开展核心素养评价的一种基本思路,欧盟国家、美国等开展了此类探索.例如,立陶宛在对学会学习素养的评价时,将其分解为学习态度与意愿、确定目标与计划活动、有组织和有针对性的活动、反思学习的活动和结果,并围绕这4个要素开发了学会学习素养评价工具[2].有些跨学科素养,如学会学习、自我调控、学习态度等无法通过标准化测试进行充分评价,这就需要探索标准化测试之外的评价方法.问卷即是国外普遍采用的方法之一,例如,欧盟对“学会学习素养”的评价框架包括情感、认知和元认知3个维度,该框架采用测试来评价认知维度,采用问卷评价情感和元认知维度.当然,评价的形式可以是多样的,包括档案袋、学生展示、实验、小组合作、项目、课程作业、日记、采访活动、角色扮演等,其中档案袋的使用越来越广泛[3].
国内许多学者在学科领域对核心素养评价指标体系作了研究,但大多是重点考查关键能力因素,没有对品格和价值观的评价指标体系作专门研究[4-7].也有一些学者的做法是将关键能力、品格与价值观放到一个体系中来构建.例如,张莹等人运用德尔菲法,通过调查和专家访谈,从学生个体需要和社会需求角度出发,构建了具有一定操作性的基于核心素养框架测评教育质量的综合指标体系,即包括学科素养、生存素养与精神素养3个领域.其中精神素养的二级指标是健康审美情趣、情感态度价值观[8].物理学科核心素养为物理观念、科学思维、实验探究、科学态度与责任.刘洋等人以布卢姆教育目标分类学为基础,构建了高中物理核心素养评价的一个体系,并将物理核心素养细化为9个层次的教学目标和内容,价值观放入其中[9].
国内对非智力因素测量的研究较多,就数学学习而言,王光明教授团队编制了贯通小学、初中、高中3个学段的学生数学学习非智力测评工具[10-12],以及与之对应的常模研究[13-15].以初中生数学学习非智力因素调查问卷为例,主要包括动机、态度、意志、性格、情绪情感5个维度,经过探索性因素分析和验证性因素分析,得到效度和信度都较好的量表[11].利用这份问卷,对天津市11个区县共1 400名初中生进行问卷调查.根据所得数据,建立初中生数学学习非智力水平总体及其子维度常模表,并确定了对应的等级评价标准[14].这些研究中,部分涉及到了品格因素,但价值观的渗透不多.
《普通高中数学课程标准(2017年版)》对评价的建议部分,在评价原则中专门列了一条“关注学生的学习态度”,并对此作了细致地解释[16].课程标准没有对品格与价值观的评价作专门论述.为了便于中小学教师在实践中对学生品格和价值观发展作评价,研究者提出了一个评价指标体系[17].包括数学价值观念、数学思维品格、数学学习态度和学会数学学习4个一级指标.数学价值观念包括科学价值、文化价值、育人价值3个二级指标;数学思维品格包括理性思维、批判质疑、勇于探究3个二级指标;数学学习态度包括乐于学习、主动学习、坚毅执着3个二级指标;学会数学学习包括合作交流、善于学习两个二级指标.在教学过程中具体操作时,可对学生的表现进行分级评价(表1).

表1 品格与价值观评价量表
结合表1,可采用给学生建立综合素质档案,指导学生客观记录成长过程,记录学生在学习和实践过程中的具体表现,考查学生的作品质量,保留和分析学生在不同时期的表现行为等过程性评价方式进行评价.
这里所做的研究是在这个评价指标体系基础上,编制适合中学生数学学科品格与价值观的问卷,作为品格与价值观评价的一个辅助工具,同时,也可作为研究学生品格与价值观课题的测量工具.
2 研究方法
2.1 问卷设计
表1的评价指标体系的建构,是选择中小学教师、教研员、数学教育专业的研究生作为被试,对38个问题的认可度问卷再通过因素分析方法得到的,是合乎科学性标准的.但另一方面,现编制的是针对中学生的问卷,有的因素可能会在原来的指标体系中产生一定变异.为了解决这个问题,研究者保留原指标体系的一级指标,不考虑二级指标,即依据一级指标编制题项,再对4个一级指标的问卷数据作因素分析,析取各一级指标下的二级指标.
4个一级指标设计的题项编号及题项数见表2.

表2 一级指标的题项编号
一共45个题项,问卷采用利克特量表.题目设计以第一人称表述,如“我认为学习数学能够训练人的逻辑思维和钻研精神”“我觉得与老师交流不是一种有效的学习方式”.被试站在自己的立场上回答问题会显得真实和贴切.
问卷的指示语“请根据你的实际情况,回答下面每一个表述在多大程度上符合你的想法”,被试在“非常符合、多半符合、一半符合、多半不符合、非常不符合”5个选项选择一个.其中2、4、6、9、12、13、14、16、18、21、23、25、26、29、33、36是反向问题.赋分方式:正向题目5、4、3、2、1;反向题目1、2、3、4、5.
2.2 被试
在江苏省普通初中选择被试,其中南京市297人,连云港市360人,共计657人.所选学校有城市学校和农村学校,有重点中学和普通中学,其中农村学校主要分布在连云港.被试具有较好的代表性.
2.3 数据处理
采用SPSS17.0软件作项目分析和因素分析.
3 研究结果
3.1 项目分析
首先,依据被试在问卷的得分进行分组,得分在前33%的为高分组,得分在后33%的为低分组.对高分组和低分组在每一个题项的得分作检验.结果显示,在45个题项上高分组和低分组均存在显著性差异.其次,计算每一道题得分与总量表分数的相关系数,删除相关不显著或相关系数低于0.4的2、5、7、10、15、18、19题.这样,就对剩下的38个题项作因子分析.在变量名称编码上,题项变量名称依然用原来的题号表示,只是被淘汰的7个题目不纳入作因素分析.
3.2 因素分析
第一步,对第一个指标对应的子量表1作因素分析(表3、表4).
根据KMO和巴特利特检验可知,KMO抽样适当性参数值为0.858,Bartlett球形检验2值显著,说明题项变量间的关系良好,可以进行因子分析.
从表5可以看出,其特征值只有2个大于1,故只提取2因子,这2个因子在碎石图的坡上(见图1),这2个共同因素可以解释总变异量为58.953%.列出转轴后的成分矩阵如表6.
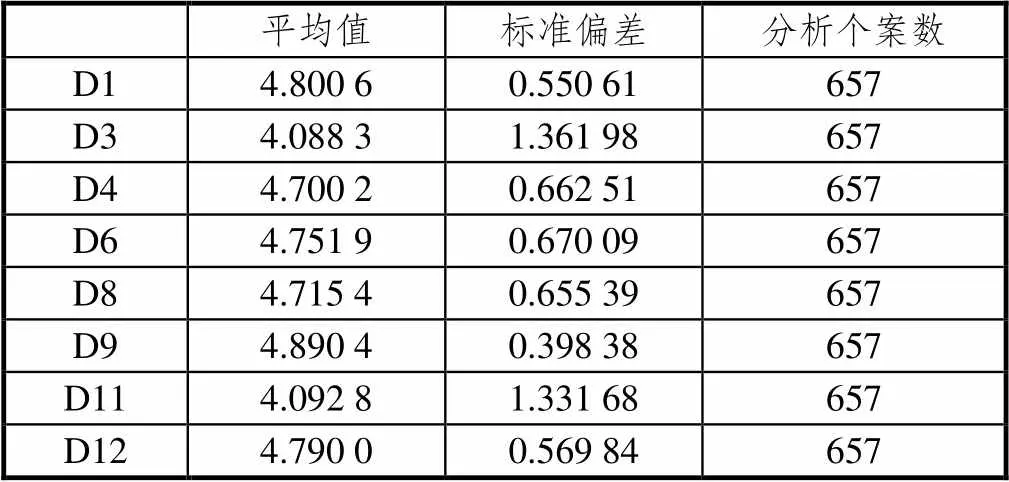
表3 描述统计

表4 KMO和巴特利特检验

表5 总方差解释
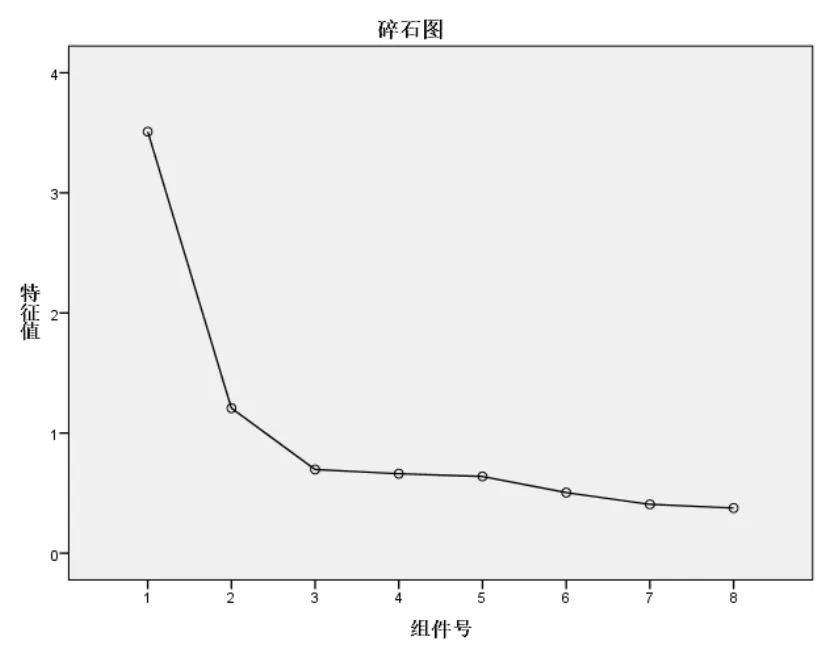
图1 碎石图

表6 旋转后的成分矩阵a
根据表6,所有题项在不同主成分上的载荷值都仅有1个大于0.4,故均可以保留.6、1、12、4、9、8这6个题项,涉及能够认识数学是其它学科的基础,数学的广泛应用性,数学在科技、社会发展中的巨大作用,能够理解数学思想方法,体会数学精神、理性思维、数学审美,并能将其转化在自己的学习行动和树立个人发展的理想信念中,所以将其命名为科学与文化价值.11、3这两个题项,涉及能够理解数学对人的思维发展的作用,形成刻苦训练、不畏艰难、积极向上的优良品格,故命名为育人价值.
第二步,对第二个指标对应的子量表2作因素分析.首先,作KMO与Bartlett球形检验.结果得到KMO值为0.804,显著性0.000,表示变量之间具有共同因素存在,变量适合进行因素分析.其次,采用主成分分析法抽取主成分的结果,转轴方法为直交转轴的最大变异法,结果见表7.

表7 总方差解释
在8个变量中特征值大于1的有2个,因此选取2个共同因素.这2个共同因素可以解释总变异量为64.079%.列出转轴后的成分矩阵如表8.

表8 旋转后的成分矩阵a
根据表8,所有题项在不同主成分上的载荷值都仅有1个大于0.4,故均可以保留.16、17、23、21这4个题项,涉及具有崇尚真理信念和求实精神,形成严谨的思维品质,能够理性地分析和解决问题,故将其命名为理性思维.22、13、20、14这4个题项涉及能够进行独立思考、独立判断、敢于质疑,有探究问题的意识,有不畏困难、坚持不懈的探索精神,故命名为探究思维.
第三步,对第三个指标对应的子量表3作因素分析.首先,作KMO与Bartlett球形检验.结果得到KMO值为0.873,显著性0.000,表示变量之间具有共同因素存在,变量适合进行因素分析.其次,采用主成分分析法抽取主成分的结果,转轴方法为直交转轴的最大变异法,结果见表9.

表9 总方差解释
在12个变量中特征值大于1的有3个,因此选取3个共同因素.这3个共同因素可以解释总变异量为62.919%.列出转轴后的成分矩阵如表10.
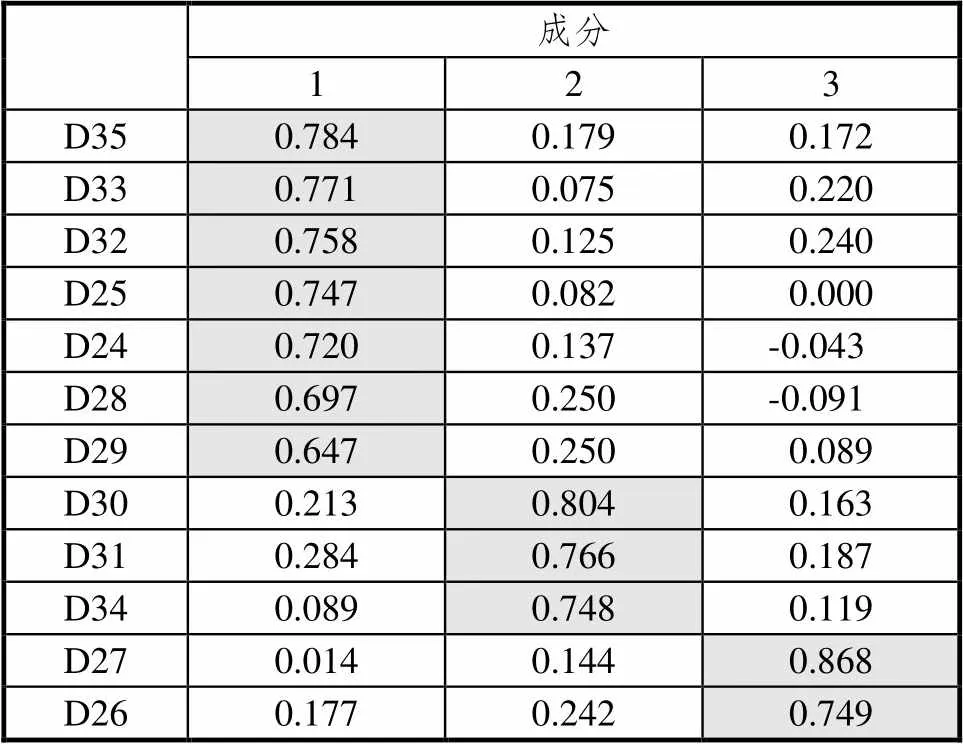
表10 旋转后的成分矩阵a
根据表10,所有题项在不同主成分上的载荷值都仅有1个大于0.4,故均可以保留.35、33、32、25、24、28、29这7个题项,涉及具有积极的学习数学动机、兴趣、自信,能够对学习结果做出正确归因,能够体会到学习的乐趣,将其命名为乐于学习.30、31、34这3个题项,涉及在数学学习中主动意识强,有积极的自主学习心态和主动学习行为,命名为主动学习.27、26这2个题项,反映出具有坚持不懈学习数学的毅力,克服学习困难与挫折的勇气,命名为坚毅执着.
第四步,对第四个指标对应的子量表4作因素分析.首先,作KMO与Bartlett球形检验.结果得到KMO值为0.880,显著性0.000,表示变量之间具有共同因素存在,变量适合进行因素分析.其次,采用主成分分析法抽取主成分的结果,转轴方法为直交转轴的最大变异法,结果见表11.
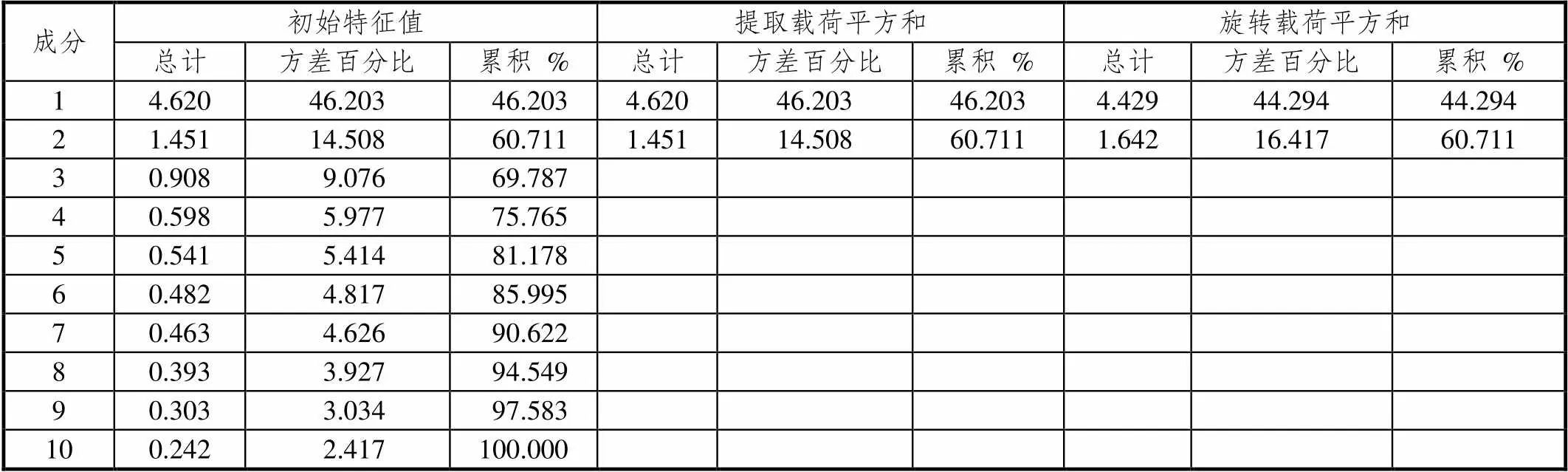
表11 总方差解释
在10个变量中特征值大于1的有2个,因此选取2个共同因素.这2个共同因素可以解释总变异量为60.711%.列出转轴后的成分矩阵如表12.

表12 旋转后的成分矩阵a
根据表12,所有题项在不同主成分上的载荷值都仅有1个大于0.4,故均可以保留.45、41、43、44这4个题项,涉及养成良好的学习态度和学习习惯,形成与他人主动合作与交流的意识和行为,将其命名为合作交流.39、36、37、42、38这5个题项,涉及具有反思习惯,善于总结经验、形成有效的学习策略,命名为善于学习.
最后,将按照上述各子量表的题项顺序,从1到38重新编号,得到初中学生数学品格与价值观的问卷(见附录).
3.3 信度与效度分析
对分量表和总量表的信度进行计算,结果如表13.数据表明量表有比较高的信度.

表13 量表的信度
因素分析的结果,保证了问卷的结构效度.进一步验证,见表14,各子量表之间的相关均小于各子量表与总量表之间的相关,因而问卷有很好的结构效度.

表14 各维度与总分的相关系数矩阵
4 讨论
问卷的设计是以文[14]的理论框架建构的,但没有选用这个评价指标体系中的二级指标,而是直接在一级指标下编拟题项,在得到公因子之后给予命名.这样就不需要作探索性因素分析,避免因探索性因素分析过程中删除题项,使题项的体量变小.因为,品格和价值观的问卷,可能需要学生回答更多的问题方能得到更加全面的信息.
在问卷的编制过程中,对题项的设计主要参考了几个方面的文献.
其一,国外关于品格的相关研究.Glanzer认为,好品格就是知善、向善和行善,包括道德知识、道德情感和道德行为3个方面,好品格包括审慎、公正、坚韧、节制[18].Wynne认为好品格包括知礼、求真、守纪、勤奋、清洁、利他[19].Rivers强调品格教育应该包括智力美德,包括学术诚实、智力勇气、责任、谦卑等[20].Bialik等人提出,品格包括6个要素:正念(自我意识)、好奇心、勇气、修复力、德行、领导力[21].还有布卢姆和威尔逊目标分类中在情意部分的相关论述.
其二,林崇德教授研究团队提的中国学生核心素养的一个框架[22].在这个框架中,与数学核心素养联系比较紧密的要素有审美情趣、理性思维、批判质疑、勇于探究、乐学善学、勤于反思、健全人格.
其三,《普通高中数学课程标准(2017年版)》中关于品格与价值观的相关论述.
参考这些资料,主要是用其中的一些关键词来编制问题,从而能够突出品格与价值观的本质属性.例如.林崇德先生关于理性思维的描述:崇尚真知,能理解和掌握基本的科学原理和方法;尊重事实和证据,有实证意识和严谨的求知态度;逻辑清晰,能运用科学的思维方式认识事物、解决问题、指导行为等.这个概念的界定就与数学品格价值观密切相关.《普通高中数学课程标准(2017年版)》描述学习态度是比较宽泛的:“在对学生学习态度的评价中,应关注主动学习、认真思考、善于交流、集中精力、坚毅执着、严谨求实等.”这本质上是对品格与价值观的写实,其用词的本意都渗透到了问卷之中.
此外,问卷编制的一个目的是为项目研究所用,而项目研究涉及“做数学”和“数学实验”,对象是初中学生,因此在题目设计时加入了一些与数学实验相关的内容.当然,问卷并不失一般性,可用于中学生数学品格与价值观的测量和作为其它研究的工具.
应当指出,对学生品格与价值观的评价不能只是利用一个问卷就能达成.品格与价值观的评价,更多地要依托过程性评价,评价形式是多样化的,如课堂观察、口头测验、完成作品、实践活动等方式,问卷调查只是其中的一种手段.
5 结论
中学生数学品格与价值观问卷包括4个一级指标数学价值观念、数学思维品格、数学学习态度、学会数学学习,分别组成4个子量表,子量表1包括科学与文化价值、育人价值两个维度;子量表2包括理性思维、探究思维两个维度;子量表3包括乐于学习、主动学习、坚毅执着3个维度;子量表4包括合作交流、善于学习两个维度.问卷有较好的结构效度和信度.
[1] 威尔逊.中学数学学习评价[M].杨晓青,译.上海:华东师范大学出版社,1989:1.
[2] 郭宝仙.核心素养评价:国际经验与启示[J].教育发展研究,2017,37(4):48-55.
[3] LOONEY J W. Assessment and innovation in education [R]. OECD Education Working Papers, OECD Publishing, 2009.
[4] 魏雄鹰,肖广德,李伟.面向学科核心素养的高中信息技术测评方式探析[J].中国电化教育,2017,38(5):15-18.
[5] 刘存芳,杨凤阳,刘民利,等.高中化学核心素养评价指标体系的建构[J].化学教与学,2019(7):2-5.
[6] 刘桂侠,王牧华,陈萍,等.地理学科核心素养评价指标体系的构建与量化研究[J].地理教学,2019(19):15-20.
[7] 于川,朱小岩,邬楠,等.高中生数学学科核心素养水平调查及分析[J].数学教育学报,2018,27(2):59-64.
[8] 张莹,冯虹.基于核心素养的教育质量评价指标体系的构建与应用[J].教育探索,2016(7):60-64.
[9] 刘洋,李贵安,王力,等.基于教育目标分类的高中物理核心素养评价[J].教育测量与评价,2017(10):35-40.
[10] 冯玉琴,王光明,李健.小学生数学学习非智力因素调查问卷的设计与编制[J].考试研究,2021,17(1):79-87.
[11] 王光明,李爽.初中生数学学习非智力因素调查问卷的编制[J].数学教育学报,2020,29(1):29-39.
[12] 王光明,宋金锦,王兆云.高中生数学学习非智力特征调查问卷的编制[J].数学教育学报,2015,24(3):17-27.
[13] 王光明,彭宇佳,李健.小学高年级学生数学学习非智力因素常模及其等级评价标准的建构与应用——以天津市为例[J].数学教育学报,2021,30(3):52-58.
[14] 王光明,李健,简婧娴.初中生数学学习非智力水平常模及其等级评价标准研究——以天津市为例[J].教育理论与实践,2020,40(20):44-48.
[15] 王光明,刘晓昱,李健.高中生数学学习非智力特征的常模及其水平等级标准研究——以天津市为例[J].天津师范大学学报(基础教育版),2017,18(3):50-59.
[16] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018:86.
[17] 喻平,赵静亚.数学核心素养中品格与价值观的评价指标体系建构[J].课程·教材·教法,2020,40(6):89-95.
[18] LICKONA T. Educating for character: The school’s highest calling [EB/OL]. (2007-04-03) [2021-07-15]. http://www. glc.k12. ga.us/passwd/trc/ttools/attach/chared/resources/speech_Lickona.pdf, 1997.
[19] WYNNE E A. Balancing character development and academics in the elementary school [J]. Phi Delta Kappan, 1988, 69 (6): 424-426.
[20] RIVERS T M. The essentials for character education [J]. The Journal of General Education, 2004, 53 (3-4): 247-260.
[21] 玛雅·比亚利克,迈克尔·伯根,查尔斯·菲德尔,等.21世纪的品格教育:学生应该学习什么(上)[J].陈伦菊,盛群力,译.数字教育,2018(10):78-84.
[22] 林崇德.中国学生核心素养研究[J].心理与行为研究,2017,15(2):145-154.
学校:___________ 姓名:___________ 性别:___________班级:___________
亲爱的同学:
请根据你的实际情况,回答下面每一个表述在多大程度上符合你的想法,每个问题只能选一个最适合的答案(在答案序号上画“√”).请你认真思考后再选择答案,谢谢!

序号表述非常符合多半符合一半符合多半不符合非常不符合 1数学知识与我们生活联系紧密,因此数学是很有用的学科. 2我认为现代技术的发展与数学没有太大关系. 3因为许多学科要用到数学知识,所以我认为一定要学好数学. 4我认为领会数学思想方法不如理解数学知识重要. 5有的数学公式和图形非常美,例如勾股定理、对称图形都很美. 6我并不崇拜数学家,因为他们的经济收入不高. 7我认为学习数学能够训练人的逻辑思维和钻研精神. 8我认为通过数学学习,可以使人养成一种追求真理的精神. 9我认为数学实验能够培养我们的动手和动脑能力. 10对别人提出的想法,我要自己想明白后才会表示同意或反对. 11当我解答问题的方法与人家不一样时,我就放弃自己的解法. 12与同学讨论数学问题时,我不敢反驳他们的观点. 13在数学课上,我感觉老师说的话都是正确的. 14每当遇到新的数学知识或数学问题,我都特别想弄明白. 15在解答问题后,我从来不去想是否还有其他解法. 16我认为数学实验是一种探究问题的好方法. 17当我努力作一道题目但没有解答出来时,我就会不再想它. 18当假期快要结束时,我盼望回到学校上数学课. 19我觉得数学不枯燥,特别是做数学实验能够激发学习兴趣. 20我学习数学的动力完全是因为中考和高考都要考数学. 21当考试成绩不佳时,我会检讨自己的不足和失误. 22当考试成绩不佳时,我总是会想是不是自己的智商太低. 23在没有老师和家长监督时,我能主动完成数学作业. 24我不知道数学实验的目的是什么,所以对数学实验不感兴趣. 25我不会主动预习第二天要上的数学课内容. 26除了完成老师布置的作业之外,我还会找一些数学题目来做. 27遇到有挑战性的数学问题,我会花了很长时间去想,直到弄懂. 28我给自己定的数学学习计划,经常坚持不下来而中途放弃. 29通过学习数学,使我养成了做一件事情坚持不懈的习惯. 30在数学实验中,我喜欢与同学一起讨论完成. 31解答数学问题时,在有了自己的想法后,我总想向别人表达. 32我觉得与老师交流不是一种有效的学习方式. 33在解决一个问题后,我会回顾解题的过程,想想有什么收获. 34每一单元结束时,即使老师没有要求,我也会自己梳理和复习. 35我觉得动手操作不是学习数学的一种好方法. 36解答应用问题时,我喜欢画一个示意图帮助理解题意. 37如果在课堂上做了数学实验,它会给我留下深刻印象. 38我习惯把当天课堂上学习的内容先复习一遍,再做家庭作业.
Questionnaire Design of Middle School Students’ Mathematical Character and Values
YU Ping1, DONG Lin-wei2, GUO Qing-song3
(1. School of Mathematical Sciences, Nanjing Normal University, Jiangsu Nanjing 210097, China;2. Education Science Planning Office of Jiangsu Province, Jiangsu Nanjing 210013, China;3. Teaching Research Office Jiangsu Provincial Department of Education, Jiangsu Nanjing 210013, China)
Based on the relevant theories, the questionnaire of middle school students’ mathematical character and values is developed. The questionnaire includes four first-level indicators: mathematical values, mathematical thinking character, mathematical learning attitude, and learning to learn mathematics, which are respectively composed of four subscales. The secondary indexes of each subscale are respectively, Subscale 1: scientific and cultural value, educational value; Subscale 2: rational thinking, inquiring thinking; Subscale 3: Willing to learn, active in learning, persistent; Subscale 4: Cooperative communication and good at learning. The questionnaire has good reliability of structure validity.
middle school students; mathematics core literacy; questionnaire; measurement
G632
A
1004-9894(2021)04-0012-07
喻平,董林伟,郭庆松.中学生数学品格与价值观的问卷设计[J].数学教育学报,2021,30(4):12-18.
2021-07-17
国家社科基金教育学一般课题——中学生学科核心素养的评价研究(BHA170150)
喻平(1956—),男,重庆人,教授,博士生导师,主要从事数学教育研究.
[责任编校:周学智、陈汉君]

