基于地震损伤次生火灾概率研究

李承玥, 王宪杰, 胡 彪, 王思文, 赵 颖

(云南大学建筑与规划学院, 昆明 650504)

据中外震害数据表明,地震引起的次生灾害中,火灾是最常见也是最危险的。继发的次生火灾往往会导致人员伤亡数量和经济损失加倍,一旦发生可能会造成广泛的破坏,更有一些实际震例表明次生火灾带来的危害比地震本身更为严重[1]。1906年美国旧金山市发生里氏8.3级地震[2],导致水管、煤气管道被毁坏,引发火灾持续燃烧了3天3夜,由次生火灾造成的损失是地震直接损失的10倍；1923年日本关东地区发生里氏8.1级地震[3],因发生时间为东京时间11∶58,住宅区内炉火使用率高,导致有336处同时起火,由次生火灾造成的人员伤亡占总伤亡人数的40%；1975年中国海城发生7.3级地震[4],由于地震局及时发布准确预报并做好应急措施,地震直接造成的伤亡人数有所减少,但震后因冻灾和防震棚起火也造成了人员伤亡,占总伤亡人数的42%。

中国位于世界两大地震带——环太平洋地震带与欧亚地震带之间,地质构造复杂,为地震频发国家之一。地震发生后,防火、灭火系统以及生命线系统被毁坏,常常引起地下管线网络的震裂泄漏以及交通堵塞、通讯中断[5-6],导致消防力大幅度下降,一旦发生火灾无法及时实施扑救会造成更多的人员伤亡和经济损失。

由于地震导致次生灾害发生这一事件具有随机性且发生概率小,可用于研究的历史震害资料不足,且地震次生火灾的研究涉及地震社会学、概率学、传热学等多种学科的交叉,相关研究展开难度较大,所以目前中外针对地震次生火灾方面的研究很少。日本学者构建回归模型,地震作用下建筑倒塌概率引发次生火灾起火次数[7],但日本木结构占多数,发生火灾的概率较大,显然这类预测模型不适合中国。李杰等[8]用泊松过程模拟地震次生火灾的发生概率,但因缺乏实际数据的验证,可靠性方面有待商榷。美国联邦紧急救援署FEMA开发的灾害评估管理系统HAZUS中,提供了峰值地面加速度与地震起火率之间的回归关系式[9]。

总结得出,目前中外对地震次生火灾的研究方法主要分为两类,一类是回归分析法,即通过对历史震害数据进行回归分析,拟合出各影响因子与地震次生火灾发生率之间的关系式；另一类是概率模型法,即通过构建概率模型预测给定超越概率下地震次生火灾的发生次数[10-13]。

现选取Park-Ang双参数损伤模型,计算一幢建筑在多遇、罕遇地震作用下的损伤程度,基于不同损伤D值范围建立针对单体建筑的地震次生火灾非确定性模型,参考文献[14]对建筑不同使用功能情况和不同损伤D值范围内的起火概率进行赋值,最终得到建筑的着火概率值。

1 地震损伤模型分析

在抗震设计中,如何选取合适的指标来描述建筑结构在地震作用下的破坏程度显得尤为重要。目前的研究主要是通过求解结构的楼层加速度、层间位移、层间位移角、滞回耗能等来表征结构的破坏程度[15-16],这些方法通常以结构的某一单一参数作为指标,不能同时考虑结构在往复荷载作用下的累积损伤和地震动对结构安全性的影响。为了弥补单参数损伤指标的不足,本文选取综合考虑结构变形与滞回耗能的Park-Ang双参数损伤模型[17-18],能更好的描述结构在地震作用下的弹塑性破坏。公式如式(1)所示:

(1)

式(1)中：D为结构的综合损伤指数,不同范围的D值对应的损伤程度如表1所示[19]；xm为实际地震作用下结构构件的最大位移；xcu为在单调荷载下结构构件的极限位移；Eh为地震作用下结构构件的累积滞回耗能；Fy为结构构件的屈服剪力；β为结构的耗能因子,按式(2)计算:

表1 钢筋混凝土框架结构D值与损伤程度

β=0.15(-0.447+0.073λ+0.24n0+0.134ρ)0.7100ρw

(2)

式(2)中:λ为构件的剪跨比；n0为轴压比；ρ为纵筋配筋率；ρw为体积配筋率,在往复荷载作用下,对于钢筋混凝土框架结构,建议取β=0.15[20]。

通过SAP2000对结构进行时程分析求出各节点的最大位移,再将构件对应节点的位移相减既得构件在地震作用下产生的最大位移xm。

1.1 柱等效屈服剪力Fy

若考虑柱构件,对于矩形截面对称配筋,由结构弹性分析[21]可得:

(3)

式(3)中：H为构件高度；My为构件的屈服弯矩。根据截面平衡条件,可得:

(4)

式(4)中:b、h0分别为构件截面的宽度和高度；η为有效截面系数；a为受压钢筋到截面边缘的距离；Ag为受拉钢筋面积；fc为混凝土最大压应力；f′g为受压钢筋应力,公式为

(5)

(6)

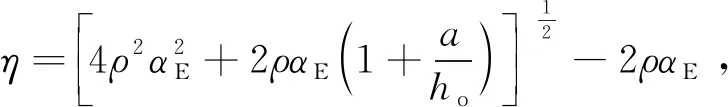
1.2 柱极限位移xcu

Park等[17-18]根据经验分析给出了计算极限位移的经验公式:

xcu=μuxy

(7)

式(7)中:μu为极限延性系数,仅考虑弯曲变形可以表示为

(8)

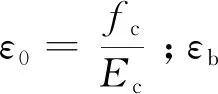
设xy为屈服位移,仅考虑弯曲变形的屈服位移可以表示为

(9)

式(9)中:屈服曲率φy=ψnφ′y,考虑混凝土的非弹性和轴向力的影响系数可以表示为

(10)

(11)

1.3 等效滞回耗能Eh

一般地,在地震作用下多自由度体系的运动平衡微分方程为

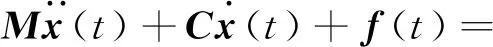
(12)

由运动方程可得恢复力方程为

(13)

通过对恢复力积分可得结构滞回耗能的增量公式[22]为

(14)

其中结构的阻尼采用瑞利阻尼模型,计算公式为

C=αM+βK

注意到，只有作为永久性资源才与时间相关，只有长时间存在的资源才会发生某些分配方法的资源非单调性(例如席位分配的哈密顿法不满足席位单调性[2])；反之，对于暂存性资源，人们往往对一次性分配仅仅关注是否与应得份额接近(紧邻性).由此可见，资源分配的宽约束模型适用于永久性资源的分配,紧约束模型适用于暂存性资源的分配.

(15)

(16)

式中:α为质量比例系数；β为刚度比例系数；ξ1、ξ2为前两阶阻尼比；w1、w2为前两阶自振频率；[K]为结构体系的矩阵。

1.4 从构件层次到结构整体

基于杨伟等[23]的试验研究结果,将每层的角柱乘1.2的放大系数、边柱乘1.1的放大系数、其余柱乘1叠加到层,分别求出每一层的最大位移、极限位移以及屈服剪力；再将薄弱层乘放大系数1.1、其余层乘1叠加到结构整体,求出xm、xcu、Fy,代入式(1)中,即可求出结构整体的损伤D值,再根据结构整体破坏程度判断地震次生火灾的发生概率。

2 地震次生火灾起火概率模型

2.1 起火原因分析

导致地震次生火灾发生的因素具有不确定性,首先地震对不同结构类型建筑物的破坏情况是不确定的,其次震后是否存在引起可燃物燃烧的点火源也是不确定的。如何定量分析这些不确定因素,需要建立数学概率模型,为地震次生火灾危险性研究提供可行方法。

针对不同使用功能的建筑结构地震后可能起火的原因不同,具体如下。

(1)针对食堂,主要是暴露的炉火及燃气等。由于地震的震动,炉具倾倒和损坏,同时燃气管道裂开导致燃气泄漏,遇到火花引起燃烧,产生次生火灾。

(2)针对实验室,主要是各类化学试剂。强烈地震时,存放试剂的容器因碰撞或掉落在地面上而导致破损或试剂脱出,进一步引发部分试剂在空气中自燃或多种试剂混合后发生化学反应产生的燃烧甚至爆炸。

(3)针对教学楼、宿舍楼等建筑,强烈地震时,建筑物变形,墙体开裂,保护层剥落,供、变电设备、室内电器及线路都有可能损坏或发生故障。震后受损的电力系统急于恢复供电可能会产生电火花,这些火花直接成为地震次生火灾的点火源,一旦遇到可燃物极易发生火灾。

2.2 单体建筑物地震次生火灾概率模型的建立

结合实地调查量化影响地震次生火灾发生的因素。首先考虑一幢建筑物内是否存在可燃物,其次建筑结构发生破坏后对这些可燃物暴露及引燃火灾概率的影响,按照这个思路建立一个针对单体建筑物地震次生火灾发生概率的一般模型:

P(F)=P(A)P(B|A)P(C|Ej)×

(17)

式中:P(F)为单体建筑物发生次生火灾的概率；P(A)为单体建筑物内是否存在可燃物,存在时取1,否则取0；P(B|A)为可燃物存在时,其可燃性影响次生火灾发生的概率；Ej为结构损伤D值；P(C|Ej)为损伤D值为Ej时,建筑物内产生着火源的概率；P(D|Ej)为损伤D值为Ej时,可燃物泄漏扩散的概率；P(G)为不同天气、季节、环境对火灾发生或蔓延的影响概率；P(B|A)为建筑物的结构类型和使用功能决定其本身是否存在可燃性材料。参考文献[24]中对不同使用功能建筑的可燃性的影响概率,将可燃性类别分为5个等级,构建针对校园区域的可燃性等级并赋值,如表2所示。

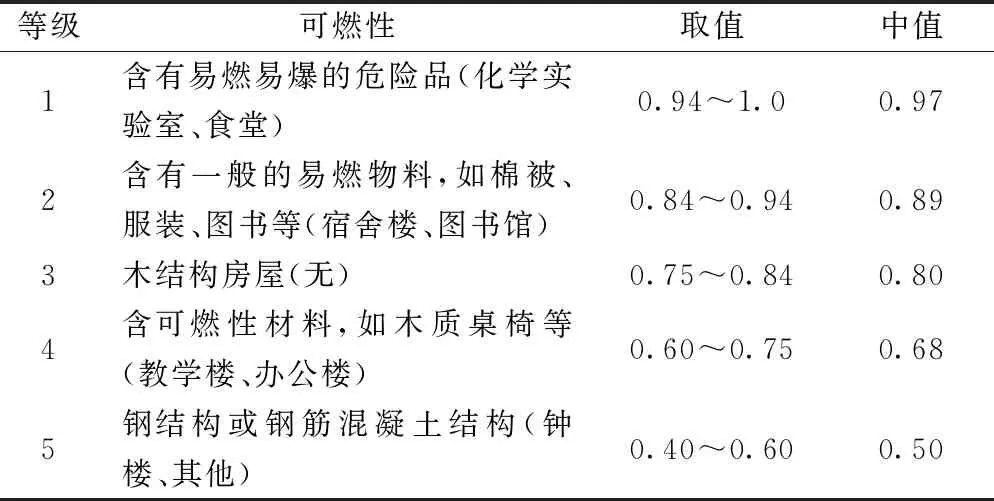
表2 建筑物内含可燃物及结构本身的可燃性

P(C|Ej)为结构的不同破坏程度对建筑物内产生着火源的概率有影响。参考文献[24]中按五种破坏等级对着火源发生的影响概率,结合本文前部分所求出的损伤D值,构建损伤D值为Ej时,建筑物内着火源发生的概率取值如表3所示。

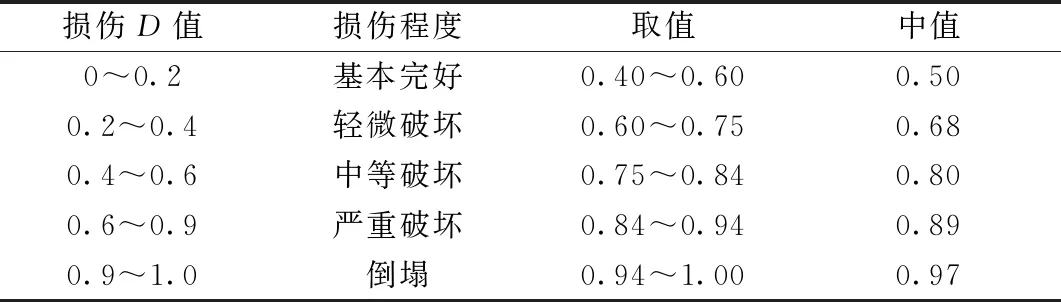
表3 不同损伤D值影响着火源发生的概率

P(D|Ej)为结构的不同破坏程度对建筑物内的可燃物泄漏扩散的概率有影响。参照P(C|Ej),构建损伤D值为Ej时,建筑物内可燃物泄漏扩散的概率取值如表4所示。

表4 不同损伤D值影响可燃物泄漏扩散的概率

P(G)为气候条件和环境对地震次生火灾的发生影响较为明显,本文选取三种具有代表性的天气环境条件,对火灾扩散蔓延的影响概率取值如表5所示。

表5 不同天气环境影响概率

3 算例分析

3.1 结构随机非线性动力时程分析

以云南大学呈贡校区内一幢6层RC框架结构为例,底层层高4.8 m,其余层层高3.9 m,总高度为24.3 m,其SAP2000计算模型如图1所示,该场地信息如表6所示。

表6 云南大学呈贡校区场地信息

图1 SAP2000有限元计算模型

采用FEMA P695推荐的5条地震波数据加2条人工波计算,地震动记录如表7所示。

表7 选取的地震动记录

按建筑抗震设计规范GB 50011—2010(2016版)将7条地震波调幅后输入SAP2000,通过编写MATLAB程序调用SAP2000对模型进行非线性时程分析,求出结构在罕遇、多遇地震作用下的损伤D值及对应的破坏等级,如表8所示。结构在罕遇地震作用下的层间位移角如图2所示。结构不同破坏等级对应的最大层间位移角参考限值如表9所示。

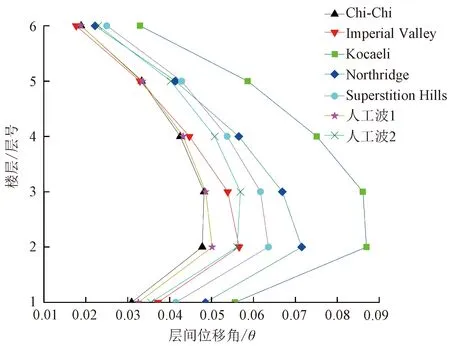
图2 罕遇地震作用下的层间位移角

表8 结构在罕遇 / 多遇作用下的损伤D值及破坏等级

算例结构在罕遇、多遇地震作用下的层间位移角及对应的破坏等级,如表10所示。

表10 结构在罕遇 / 多遇作用下的层间位移角及破坏等级

对比表7与表9可知,以损伤D值为指标得出的破坏等级比以层间位移角为指标的一致,但以D值作为判断次生火灾发生概率更具有安全性。

表9 最大层间位移角限值

3.2 起火概率分析

因在多遇地震下结构损伤D值处于0.08～0.15范围内,此时结构基本完好或局部轻微损坏产生微小裂缝,发生次生火灾的概率较低,此处不考虑多遇地震工况仅考虑罕遇地震工况。按照第2节地震次生火灾起火概率模型所述方法,首先假定建筑物内存在可燃物,即P(A)=1,且晴天、炎热、干燥、风大、房屋密集的天气环境下,计算建筑物在各种工况条件下的起火概率值如表11所示。

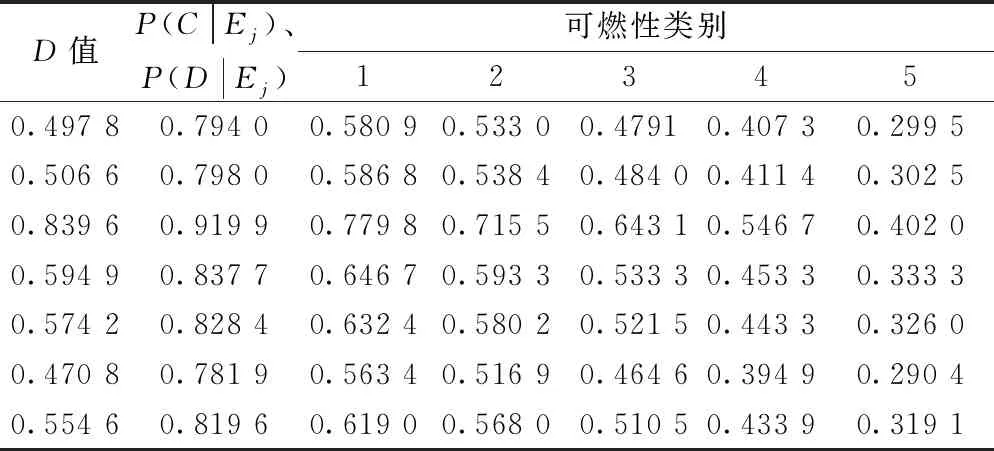
表11 建筑物的起火概率值

假定建筑物地震次生火灾的起火概率阈值为0.6,则在罕遇作用下,该建筑物有6种工况的着火概率在阈值以上,其中有4例发生在可燃性类等级为1时,即建筑使用功能为的含有易燃易爆化学危险品的实验室或正在使用炉火的食堂内；有3例发生在损伤D值为0.839 6,即建筑严重破坏时。

4 结论

本文综合考虑结构位移变形及滞回耗能两方面,选用Park-Ang双参数损伤模型描述结构或者结构构件在地震作用下的损伤情况,并基于算例分析得到以下结论:

(1)根据Park-Ang模型求解损伤D值判断结构的破坏程度和以层间位移角为指标判断结构的破坏等级结果一致。基于损伤D值进行次生火灾研究综合考虑了结构的位移变形及滞回耗能,更准确地表征结构在地震作用下的损伤情况。

(2)通过构建单体建筑物地震次生火灾概率模型,得出在罕遇地震作用下,含有易燃易爆化学危险品的实验室和正在使用炉火的食堂发生火灾的概率最高,学校需要对这类建筑加强消防措施；对于含大量棉织物品的学生宿舍楼以及含大量木质桌椅的教室,必要的消防措施也不可忽视。

该模型求出的着火概率值,能反映不同使用功能的建筑的地震次生火灾发生概率,为后期次生火灾的防御对策乃至应急措施的制订提供指导方针。