基于多元线性回归模型的湖南省粮食产量的影响因素分析

□ 杨 威（邵阳职业技术学院公共课部，湖南 邵阳 422000）

民以食为天，随着中美贸易摩擦的不断升级以及新冠肺炎疫情的影响，中国的粮食产量问题应该引起高度重视，湖南作为传统的农业大省，同时地处华中地区，拥有独特的战略地位，加上湖南省的环境适宜，历来是中国的粮食生产大省。在当前的经济形势之下，研究湖南省的农业生产显得尤为重要。通过分析湖南省粮食产量的主要影响因素，有利于我们进一步为提高湖南省的粮食产量进言献策［1］。

本文通过建立多元线性回归模型，利用2008-2018年湖南省粮食产量的数据，所有数据均来源于湖南省统计年鉴（http：//222.240.193.190/19tjnj/indexch.htm），试图找出对湖南省粮食产量的主要影响因素，并提出相关政策建议。

一、多元线性回归模型简介

多元线性回归模型是描述因变量y如何依赖于自变量x1，x2，…，xm和误差项的方程，它的一般形式为：

其中，y为因变量；x1，x2，…，xm为自变量，有m+1个未知参数，ε是随机误差项，误差项反映的是除x1，x2，…，xm与y的线性关系以外的随机因素对的影响。一般地，对误差项ε有如下三个假定：

（1）ε是期望值为0的随机变量，即E（ε）=0；

（2）对x1，x2，…，xm的所有值，ε的方差σ2都相同；

（3）服从正态分布，且相互独立，即ε～N（0，σ2）。

由模型的假定，可得多元线性回归方程：

E（y）=β0+β1x1+…+βmxm+ε

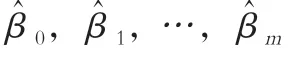
用β0，β1，…，βm去估计回归方程中的参数时，便得到了估计的多元回归方程：

多元线性回归模型初步建立后，是否真正解释了自变量与因变量的关系，还要进行显著性检验，包括对回归方程的拟合优度、回归方程线性关系的显著性、回归系数的显著性等统计量的检验后，才可以用于解释、分析实际问题。如果进行假设检验的结果不好，则需要对模型进行修正［2］。

二、模型的构建与检验

本文选取湖南省的每公顷面积粮食产量（千克）为被解释变量y，以如下指标作为解释变量：x1为农业机械总动力（万千瓦），x2为有限灌溉面积（千公顷），x3为化肥施用量（万吨），x4为农村用电量（亿千瓦小时）。根据所选指标，初步建立湖南省的每公顷面积粮食产量与农业机械总动力、有限灌溉面积、化肥施用量、农村用电量之间的多元线性回归方程，模型为：

y=β0+β1x1+β2x2+β3x3+β4x4+ε

其中，β0，β1，β3，β4为方程中的未知参数，ε是随机误差项。

用SPSS25.0进行分析得到方差分析表，如表1所示，表中第二个模型的F值为7.461，P值为0.015＜0.05，说明列入模型的各个自变量联合起来对因变量有显著影响，即有限灌溉、化肥施用量对湖南省每公顷面积粮食产量有显著影响。

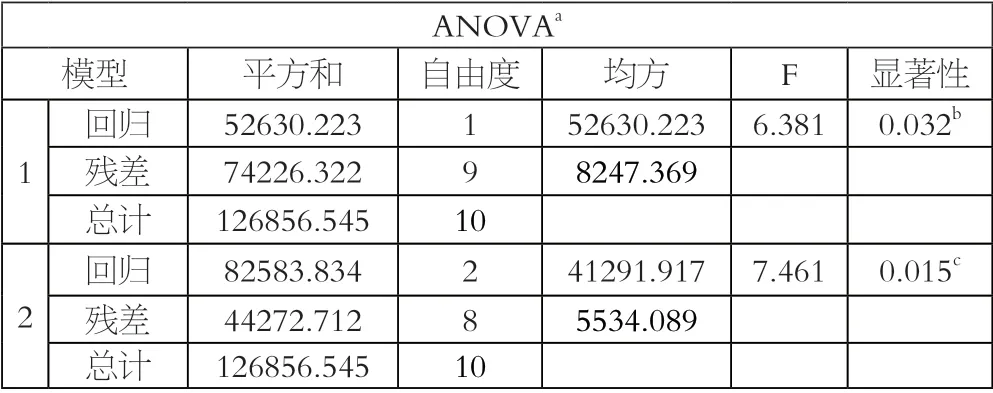
表1 方差分析表

表2主要呈现出回归模型的回归系数以及显著性检验、共线性诊断等数据，由此得到的模型为：

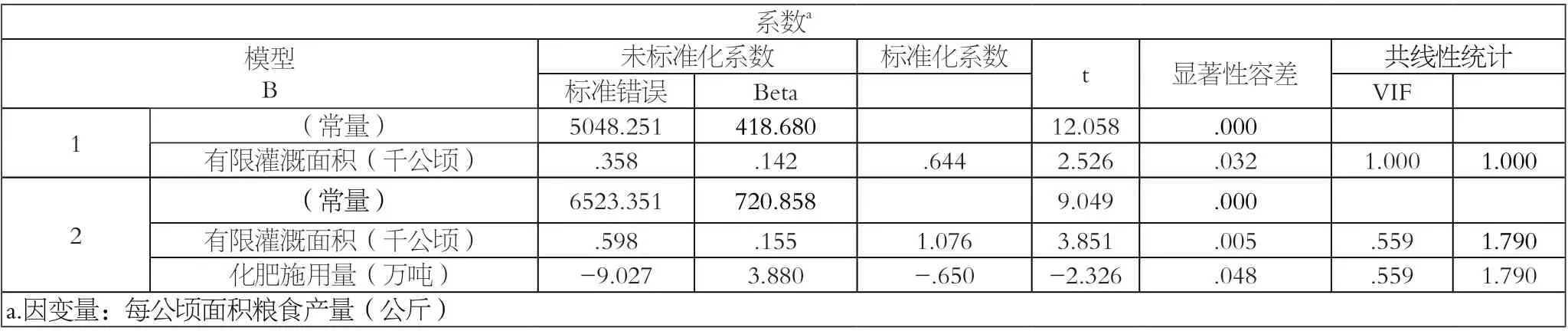
表2 湖南省粮食产量逐步回归结果

y^=6523.35+0.598x2-9.027x3

表中第二个模型的t检验所对用的P值均小于0.05，这说明有限灌溉面积和化肥施用量对湖南省每公顷面积粮食产量有显著影响。有限灌溉面积的标准化系数Beta相比化肥施用量的标准化系数Beta更大，说明有限灌溉面积较化肥施用量来说，其对湖南省每公顷面积粮食产量影响更大。

对回归模型共线性的诊断：虽然自变量对因变量的影响显著，但自变量之间可能存在相关性，即出现多重共线性问题，这会影响对自变量贡献率的评价；因此需要对回归方程中的自变量进行共线性诊断。方差膨胀因子（VIF）是指自变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比，该数值为容忍度的倒数。VIF值越大，则共线性问题越严重。当VIF＞10时，说明存在强共线性关系［3］。由表2可以看出，模型2中各变量的VIF值均为1.79，远小于10；因此，在该模型中变量之间的共线关系不显著。

图1和图2分别是回归标准化残差的直方图和散点图，从图1和图2可以看出：残差基本符合正态分布，这表明多元线性回归方程的拟合效果良好。

三、结论与政策建议

本文对湖南省粮食产量的影响因素进行了实证分析。从分析结果可以得出以下结论：在2008-2018年期间，影响湖南省粮食总产量的因素主要是有限灌溉面积和化肥施用量。其中，有限灌溉面积比化肥施用量对湖南省粮食产量的影响要大。为此我们提出以下政策建议：首先，要确保湖南粮食主产区的水利设施建设完善，加大农业基础设施建设，兴建水库，预防水灾旱灾；其次，加强灌溉知识教育，通过传授先进的灌溉技术，增强灌溉效率；最后，对于化肥施用量要进行控制。