速度极值的计算方法探讨——以复合场中带电体类斜抛运动为例

(江苏省句容高级中学，江苏 镇江 212400)

1 引言

复合场中的类抛体运动是高中物理选修部分的重要内容，其动力学问题是高考的重点与难点。近年来，物理教学工作者对此进行了一定的研究，包括直线与曲线运动模型的构建、解析方法的归纳与优化、虚拟仿真实验的引入与应用等。本文从运动学、力学、数学函数、几何向量等方面，对复合场中做类抛体运动的带电体速度极值的计算方法加以分析与归纳。

2 问题情境

如图1所示，在竖直平面内放置着绝缘轨道ABC，AB部分是半径R=0.40m的光滑半圆形轨道，BC轨道所在的竖直平面内分布着E=3.0×103V/m的水平向右的有界匀强电场，AB为电场的左侧竖直边界。不计空气阻力，现将一质量m=0.4kg、电荷量q=-1×10-3C的滑块(可视为质点)从BC上的某点由静止释放，通过A点时对轨道的压力恰好为零。滑块离开半圆形轨道后进入匀强电场，在重力G与电场力F的共同作用下做类斜抛运动(图2)。

图1

图2

3 速度极值的计算方法

3.1 利用运动的合成与分解

图3

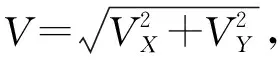
3.2 利用二次函数计算极值

3.3 利用向量点乘计算极值

如图4所示，滑块离开A点后做匀变速曲线运动，其所受合力F合的方向与瞬时速度V的方向的夹角从钝角变为直角再到锐角。滑块瞬时速度V的大小变化为先减小后增大，具有最小值。当F合的方向与V的方向垂直时，即F合·V=0时，V取最小值。

图4

4 结语

本文以复合场中类抛体运动为例，从运动的合成与分解、二次函数求极值、向量点乘等角度，对带电体速度极值的计算方法加以分析与归纳，拓展了解题思路，提高了学生运用数学解题的能力。