拉普拉斯变换在碳循环以及相关问题中的应用
李喜彬, 麻嘉欣, 石璐洁, 麻 欢, 张雅雯
(1.内蒙古师范大学 物理与电子信息学院,内蒙古 呼和浩特 010022;2.内蒙古师范大学 应用数学中心,内蒙古 呼和浩特 010022)
1 拉普拉斯变换在碳循环模型中的应用
1.1 动力学方程
大气中CO2主要来源于人类排放,如化石燃料SFOSS以及土地利用变化SLUCF(农业、林业等)。地球生态系统碳循环主要通过二氧化碳的形式进行,了解碳循环非常重要。由于海洋的吸收,大气中的二氧化碳浓度会被逐渐稀释,其流量记为ΦOCN,陆生植物的稀释流量记为ΦBIO。利用响应函数来描述碳循环的行为可以追溯到很多年前,该过程可以通过一个积分方程表示[1]
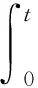
(1)
其中:Q(t)表示大气中二氧化碳的总质量;R(t)为响应函数表示排放大气中剩余碳的比例;S(t)表示二氧化碳的排放率,为化石能源和陆地生态系统的排放总和,S(t)=SFOSS(t)+SLUCF(t)。这里假设Q和S的初始条件为Q(0)=0和R(0)=1。对方程(1)两端求关于时间的导数,得到[2]
(2)
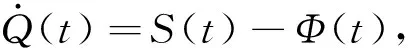
(3)
如果考虑温度变化对大气二氧化碳总量的影响,(1)式可以进一步写为[3]
(4)
其中H(t)为二氧化碳排放率对温度W(t)的响应函数。对(1)式进行拉普拉斯变换[4]
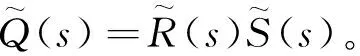
(5)
(6)
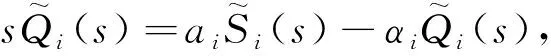
(7)
其中ai就可以视为不同二氧化碳源的比例。对(7)式进行拉普拉斯逆变换,就得到微分方程
(8)
常微分方程(8)给出了求解大气二氧化碳总量的一种方法[5]。
如果排放率为指数形式S(t)=Aexp (βt),拉普拉斯变换为一个单极点的形式
(9)
并且这个单极点主导了方程的演化趋势。大气中二氧化碳馏分(airborne fraction)定义为二氧化碳对时间的变化率与二氧化碳排放量之比,由拉普拉斯逆变换可知[6]
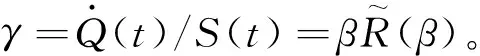
(10)
在这种情况下,同样可以得到大气中二氧化碳总量的解为[7]
(11)
1.2 动态过程
如前文所述,碳循环主要包含两部分:海洋和陆地生物群。如果考虑一个碳库总量Q对另外一个碳库流量Φ的相应,其响应函数分别为ROCN(t)和RBIO(t),表示海洋和陆地植物对进入大气的净碳通量的响应方式。拉普拉斯变换形式的方程大致可以写为
(12)
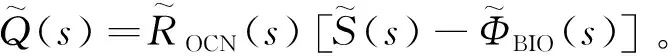
(13)
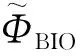
(14)
于是可以得到总的响应函数的拉普拉斯变换表达式
(15)
这个表达式最初由Enting等[8]得到。利用(15)式同样可以得到二氧化碳的馏分
(16)
其中μBIO和μOCN分别表示陆地系统和海洋系统对大气中二氧化碳增量的贡献,Oeschger 等[9]使用稀释因子(dilution factors)描述了这种分配过程,并指出了其对排放增长率的依赖性,但没有使用拉普拉斯变换。随后拉普拉斯变换被引入这个模型之中[8]。
2 拉普拉斯变换在两体阻尼振荡系统中的应用
在物理问题中经常出现由弹簧连接的两个物体,这种模型的描述如图1所示。假设质量为m1和m2的两个物体分别由具有恢复系数k的弹簧连接。把弹簧拉长至b,其原长是a,同时释放两个物体,坐标x1和x2表示两个物体m1和m2相对于释放处的位移。同时假定阻尼力与它的速度成正比,阻尼系数为γ。用上述物理量描述系统的动态方程为
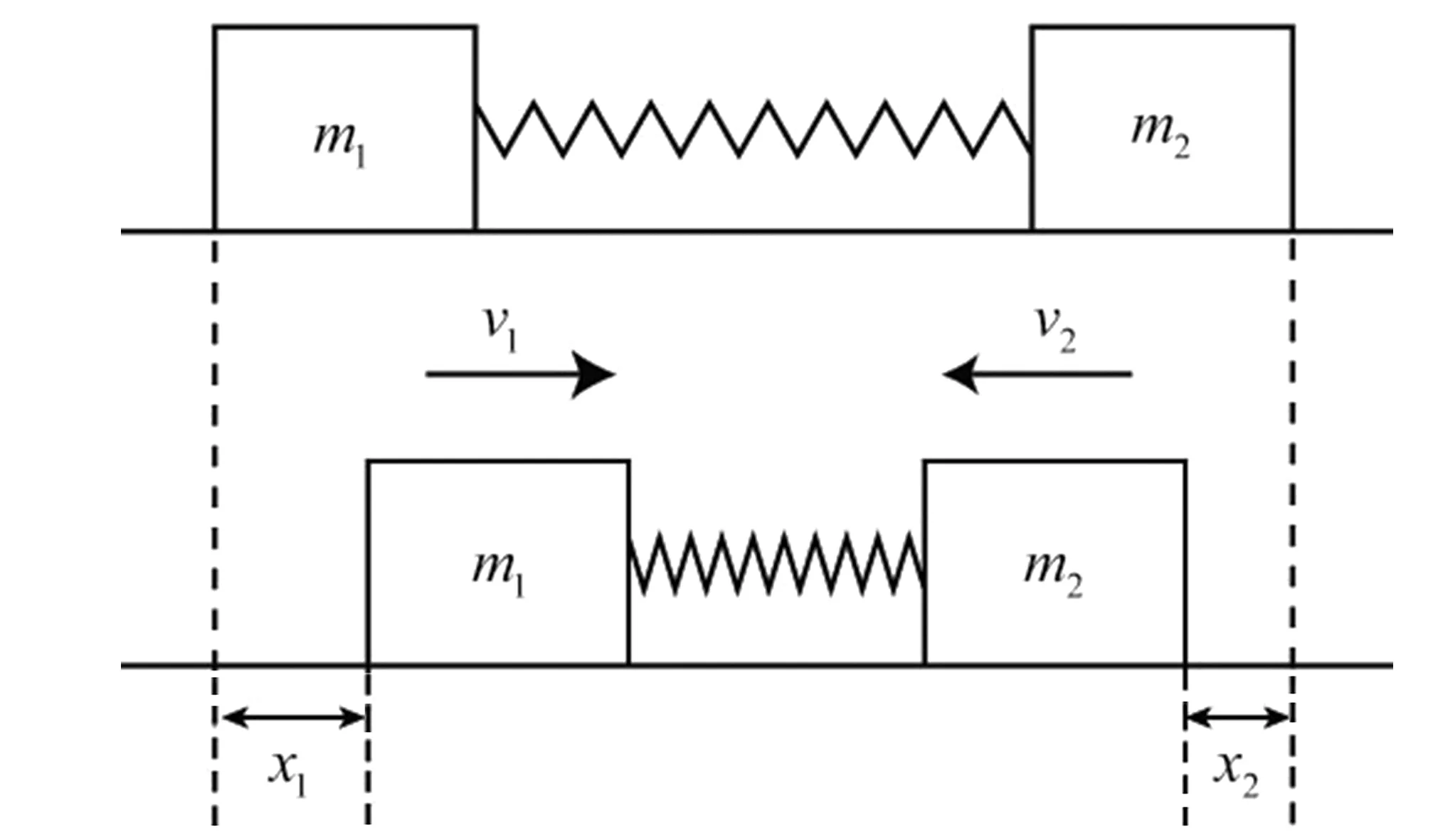
图1 运动方程(17)式对应的示意图 Fig.1 Schematic diagram of equation of motion (17)
(17)
其中初始条件为
并定义新的参数A=k(b-a)。其拉普拉斯变换为
(18)
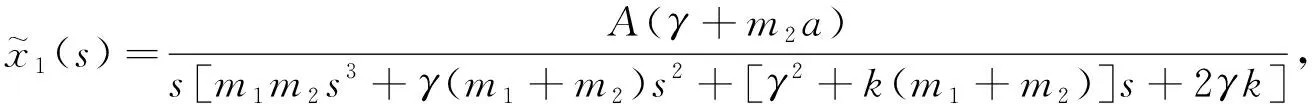
(19)
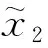
(20)
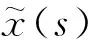
f(s)=m1m2s3+γ(m1+m2)s2+γ2s+
k(m1+m2)s+2γk=as3+bs2+cs+d
(21)
的零点处,这是一个一元三次函数。容易验证,方程f(z)=0实根和虚根的实部均为负值。
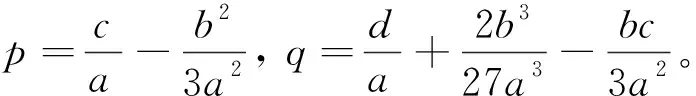
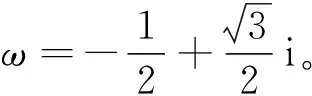
1.如果Δ=0,有三个实根且至少两个相等,这种情况对应临界阻尼振荡;
2.如果Δ<0,有三个不同的实根,对应过阻尼振荡;
3.如果Δ>0,有一个实根和两个共轭虚根,对应欠阻尼振荡。
三种振荡模式示意图如图2所示。
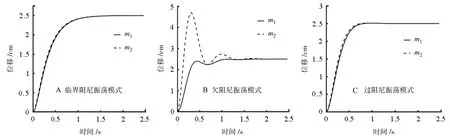
图2 三种震荡模式示意图Fig.2 The sketch maps of three damped oscillation
3 拉普拉斯变换在其他领域的应用
此算例只是给出了拉普拉斯变换在解线性齐次偏微分方程组的一个应用实例。实际上拉普拉斯变换在诸多领域都有广泛应用,比如计算某些类型的积分[11]、某些类型的积分方程[12]、线性偏微分方程[13]等问题,而且在通信类、控制类、电气类等专业课中也应用广泛[14-15]。因此,在数学物理方法的教学实践中,适当加入拉普拉斯变换对于开拓学生的视野、培养学生的学习热情都大有裨益。
3.1 拉普拉斯变换在高等数学中的应用
由上述计算可知,拉普拉斯变换对解决线性常微分方程十分方便。对于大学教学课程中的具体问题,比如在《高等数学(上册)》第七章中关于线性二阶常微分方程部分的内容,如果没有拉普拉斯变换的相关知识,可能无法理解该方程齐次部分的特征方程为什么是r2+pr+q=0这种形式[16],同样无法解释为什么在发生共振时方程的解正比于时间t:x(t)=Asin (kt+φ)-(ht/2k) coskt。拉普拉斯变换另外的一个作用便是解某些类型的积分方程,例如[12]
这类带有特定初始条件的积分微分方程,利用拉普拉斯变换以及卷积定理便可以很容易地进行求解。除此之外,拉普拉斯变换还可以用来计算某些形式的广义积分[11]。
3.2 在自动控制理论中的应用
拉普拉斯变换在“自动控制原理”课程中也起着重要作用[17]。如果能够透彻掌握拉普拉斯变换,会加深对自动控制原理中知识点的理解。拉普拉斯变换在自动控制理论中最常见的应用是传递函数,其定义为线性系统在零初始条件下,系统输出量的拉普拉斯变换与系统输入量拉普拉斯变换的比值[18],可写为如下形式:
G(s)的极点界定了系统运动的模态,而零点决定了各个模态所占的比重(通过拉普拉斯逆变换可以很容易验证这些观点)。
一个特殊应用实例为锁相环,它是由鉴相器、环路滤波器以及压控振荡器构成的反馈系统,其功能便是对输入信号的跟踪锁定。如果滤波器为低通滤波器,通过拉普拉斯逆变换可以得到一维Kuramoto方程[19]
这便是描述相位捕获的方程,系统在ω
3.3 在等离子体物理中的应用
拉普拉斯变换最大优势之一便是在变换的过程中考虑了初始条件。在一些特定的问题中,需要考虑初始条件对系统的影响,这时拉普拉斯变换便可以发挥出它的作用。比如在等离子体中需要考虑初始扰动对系统状态的影响,用Vlasov方程描述这一问题[21]
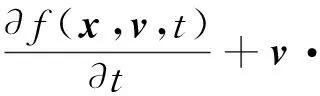
并且带有初始扰动n(x,v,0)=n0(v)+g(x,v)。对空间坐标做傅里叶变换同时对时间坐标做拉普拉斯变换,最后可以得到等离子体中电势能分布对初始扰动的弛豫关系为
(23)
χ中包含了对初始条件的积分,εl为纵向极化率,其零点均位于左半平面。由留数定理可知,(23)式中的电势能φk(t)会随着时间增长呈指数衰减,换言之等离子体系统的电磁学扰动会被耗散掉,即朗道阻尼现象。
综上所述,本文总结了拉普拉斯变换在众多领域中的应用,包括生态碳循环、两体阻尼振荡系统、微分(积分)方程、自动控制理论、等离子体物理等,展示了拉普拉斯变换在解决实际应用问题中的优势。

