基于针刺仪平稳卡尔曼滤波器的树木年龄估计*

潘 虹 卢 军 雷相东 郭旭展 姚建峰 唐守正

(1.中国林业科学研究院资源信息研究所 北京 100091；2.信阳师范学院数学与统计学院 信阳 464000)

树木年龄是森林资源调查的重要因子，可为确定合理采伐量、制定林业规划和更加科学的森林经营措施等提供重要依据，在考古学、气候学、灾害学等方面也有广泛应用(Bollschweileretal.，2010；D′Arrigoetal.，2010；Fangetal.，2012)。活立木年龄微损测量是目前林业生产和研究中最重要、最基础的共性难题，是解决很多林业问题的关键，如预测木材产量和森林碳储量、确定树木经济价值、制定古树保护措施以及古树保护等级划分等(Halletal.，2004；Thurigetal.，2005；Micheletal.，2009)，对森林管护、森林经营和古树保护等均具有重要的理论和现实意义。

确定树木年龄最准确的方法是识别树木年轮数(Wongetal.，2001；Rozas，2003)，通常采用生长锥测定法、解析木圆盘测定法、显微镜获取年轮法等，但这些方法取样基于生长芯或树干横截面，会破坏树木生长。无损的树木年龄确定方法有查数轮生枝法(吴斡宁等，2013)、建立线性生长模型(Careyetal.，2000；Loewensteinetal.，2000；Trotsiuketal.，2012)或非线性数学模型(Oberhuberetal.，2000；Rohneretal.，2013；潘虹等，2020)，但该类方法不具有普遍性且准确性也较低(Loewensteinetal.，2000；Rohneretal.，2013)。基于目前树木年龄确定方法的不足以及我国现行天然林保护的大环境，寻求一种微损测定树木年龄的方法是亟待解决的问题。

德国RINNTECH公司生产的针刺仪可以估计树木年龄、树木生长率(Orozco-Aguilaretal.，2018；Ohetal.，2019)以及腐朽程度(岳小泉，2017)。针刺仪测定树木年龄无需样本处理，对活立木伤害小，是微损的；但由于研究环境、操作者、仪器等因素影响针刺仪测量的灵敏度(Ukrainetzetal.，2010)，观测数据中存在干扰噪声，利用针刺仪自带DECOM软件检测年轮边界时(Chantreetal.，1997)很多真实年轮边界不能准确识别，使得针刺仪应用于树木年轮微损测定具有一定的局限性。而对针刺仪获取的抗钻阻力值序列进行数据分析，快速直接地估计树木年龄，可以推进树木年龄微损测定的研究进程(潘虹等，2021)。

卡尔曼滤波器本质上是一组数学方程，为最小二乘法提供有效的递归解，支持过去、现在和未来状态的估计。卡尔曼滤波是统计估计理论的里程碑，是处理噪声的有利武器(Kalman，1960)，可应用于白噪声激励的任何平稳或非平稳随机向量的估计，所得估计在线性估计中精度最佳(黄小平等，2015)。利用卡尔曼滤波器的去噪功能，处理抗钻阻力值序列的干扰噪声，可为更准确地估计树木年龄做好数据准备。

鉴于此，本研究以德国RINNTECH公司生产的针刺仪(Resistograph 4452P/S)钻入活力木获取的抗钻阻力值序列为研究样本，基于卡尔曼滤波器时间更新方程和观测更新方程，在理论上推导出针刺仪平稳卡尔曼滤波器，将平稳卡尔曼滤波器应用于活力木抗钻阻力值序列估计活立木年龄，并通过大量数据验证算法的准确性，以期为活立木年龄估计提供方法和依据。

1 基本思想

针刺仪钻入活立木获得的序列号用进针深度表示，由于进针是匀速的，因此可将序列号看作进针时刻，这样抗钻阻力值序列就可以看作一组离散时间信号，每株活立木都对应一组离散时间信号。直观上来看，信号波峰波谷振幅差别较大，有很多振幅很小的波峰波谷，并不是所有成对出现的波峰波谷均能代表年轮边界，如图1所示。这说明原始信号存在噪声干扰，去除不代表年轮变化的波峰波谷，也就是去除离散时间信号的噪声，成为判断树木年轮边界的一个关键点。

图1 活立木抗钻阻力剖面与树芯年轮对比Fig.1 Comparison of drilling resistance profile and core ring of standing tree

为了利用卡尔曼滤波器的去噪功能处理针刺仪抗钻阻力值序列的干扰噪声，本研究在卡尔曼滤波器原理的基础上，将针刺仪看作一个系统，给出针刺仪卡尔曼滤波器，同时根据其特有性质进行理论推导，提出针刺仪简单卡尔曼滤波器、针刺仪平稳卡尔曼滤波器。其基本思想是采用针刺仪信号与噪声的状态空间模型，利用针刺仪抗钻阻力前一时刻的估计值和现时刻的观测值更新对状态变量的估计，求出抗钻阻力现在时刻的最优估计值。

2 针刺仪卡尔曼滤波算法推导

2.1 针刺仪卡尔曼滤波器

将针刺仪看作一个系统，针刺仪钻入活立木获取的相对阻力剖面记录为序列z={z1,z2,z3,···,zk,···,zn}，n为针刺仪测量点的序列号，也可以看作n时刻(潘虹等，2021)。这是一组离散时间信号，信号中第k时刻的抗钻阻力观测值为zk。设针刺仪系统的状态方程和观测方程分别为：

xk=Axk-1+wk-1；

(1)

zk=Hxk+vk。

(2)

式中：xk∈Rn为第k时刻的抗钻阻力状态向量；zk∈Rm为第k时刻的抗钻阻力实测值；wk为随机噪声向量；vk为观测噪声向量。称式(1)为针刺仪的状态方程、式(2)为针刺仪的观测方程，称A为状态转移矩阵、H为观测矩阵。

基本假设1：随机信号wk和vk分别表示针刺仪过程激励噪声和观测噪声，假设wk和vk相互独立，且wk-1～N(0,Q)，vk-1～N(0,R)。

基本假设2：设相对抗钻阻力的初始状态值为x0，且x0不相关于wk和vk，

E(x0)=μ0,E[(x0-μ0)(x0-μ0)T]=P0。

(3)

式中：E表示均值。

基本假设3：设针刺仪的状态转移矩阵和观测矩阵均为1，即A=1、H=1。

(4)

(5)

定理1(针刺仪卡尔曼滤波器) 在式(1)和(2)以及基本假设1～3下，递推针刺仪卡尔曼滤波器如下。

1)针刺仪时间更新方程——向前推算当前时刻抗钻阻力值误差协方差估计的值，构造下一时刻抗钻阻力值的先验估计：

(6)

(7)

2)针刺仪观测更新方程——根据抗钻阻力先验估计值和新的抗钻阻力实测值得到改进后的抗钻阻力后验估计值：

(8)

(9)

(10)

图2 针刺仪卡尔曼滤波器算法流程Fig.2 Kalman filter flow chart of calculating k time estimated value from k-1 time estimated value

2.2 简化针刺仪卡尔曼滤波器

(11)

(12)

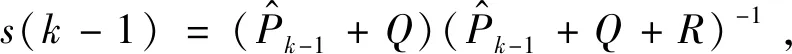
(13)

(14)

(15)

定理2(简化针刺仪卡尔曼滤波器) 在式(1)和(2)以及基本假设1～3下，简化针刺仪卡尔曼滤波器递推公式如下。

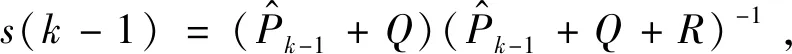
(16)

(17)

(18)

2.3 针刺仪平稳卡尔曼滤波器

在简化针刺仪卡尔曼滤波中，抗钻阻力后验估计值和后验协方差的计算仅依赖于后验信息，去掉其前验估计值和前验协方差的自回归计算，使得繁琐的计算过程得到简化，但仍需要设置4个初始参数：Q、R、x0、P0，每个参数与最终结果之间的关系难以掌握。因此考虑从后验协方差存在上下确界这条性质入手，进一步研究简化针刺仪卡尔曼滤波器，提出针刺仪平稳卡尔曼滤波器的概念，简化参数输入，且给出抗钻阻力值序列最优估计值的准确表达式。

(19)

将式(19)代入式(12)，可得后验估计值的另外一个表达式：

(20)

定理3(平稳卡尔曼滤波器) 在式(1)和(2)以及基本假设1～3下，假设初始条件为：

简化递推卡尔曼滤波器可以表示为：

(21)

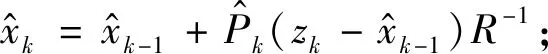
(22)

(23)

定理4 平稳卡尔曼滤波器等价于离散差分方程：

x[k]-sx[k-1]=(1-s)z[k]。

(24)

其解为：

(25)

移项得：

得到平稳卡尔曼滤波器的离散差分方程如下：

x[k]-sx[k-1]=(1-s)z[k]。

利用卷积法，求以上常系数差分方程的解为式(25)。

推论 针刺仪测量阻力值{z1,z2,…,zn}经平稳卡尔曼滤波器处理后，得到相应的最优解：

(26)

2.4 算法步骤

第一步，赋初始值,Q=1,R=Rat，Rat为常数，

(27)

第二步，对于k=2,3,4,…,n，令

s=(P+Q)(P+Q+R)-1；

(28)

(29)

依次计算zk的后验估计值：

(30)

以上算法步骤通过MATLAB编程实现，相应的伪代码如下：

输入：研究样本z={z1,z2,···,zn}；参数Rat；

过程：

2)fori=2,3,…,ndo；

4)end；

5)赋初始值t=0；

6)forl=2,3,…,ndo；

7)赋初始值tmax=0,tmin=0；

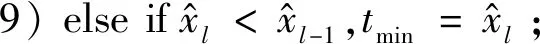
11)if |tmax-tmin|>0；

12)t=t+1；

13)end；

14)end；

15)end。

输出：样本集峰点个数t。

3 案例分析

3.1 数据获取

以山西省羊圈沟林场华北落叶松(Larixprincipis-rupprechtii)为研究对象。2017年10月，在林场华北落叶松人工林(初植密度3 300 株·hm-2)中按径阶大、中、小至少各选3株，优势木各选2株，共52株样木进行针刺试验。同一样区相同径阶样木按坡位上、中、下至少各选1株用喷漆标记编号，并详细记录样木相对位置，所选取样木尽可能树干通直、饱满、无病虫害、不断梢且生长良好。在每株样木胸径1.3 m处用针刺仪从4个方向钻入，获取有效抗钻阻力数据208组。2018年6月，在相同样木上用针刺仪在0.2 m和0.5 m处从2个方向钻入，获取有效抗钻阻力数据115组。2次试验共获取有效抗钻阻力数据323组作为研究样本。伐倒针刺样木，在针刺位置5 cm内截取圆盘，共获取104个有效圆盘作为参考样本，圆盘进行抛光、打磨、扫描，用WinDENDRO年轮分析系统结合人工判读方式获取圆盘年轮数(潘虹等，2020)。

3.2 试验结果

以针刺仪钻入活立木获取的抗钻阻力数据作为输入，经过针刺仪平稳卡尔曼滤波器后，输出为相应的抗钻阻力最优估计值序列，相比抗钻阻力原始数据，可较好地去除噪声，原来较小的波峰波谷进行了平滑处理，且保持了原始数据的波峰波谷走势。以数据编号1702的阻力折线图为例，将原始阻力数据折线图与滤波后的折线图进行对比，并将折线的部分图进行放大，见图3。

图3 原始抗钻阻力值与滤波后最优估计值的差值比较Fig.3 Comparison of the difference between the original drilling resistance value and the optimal estimated value after filtering

对104个圆盘进行试验，起始圆盘直径为8 cm，以6 cm为1个径阶，选择相应参数Rat值的依据见表1。

表1 参数Rat选择依据Tab.1 The basis of parameter Rat selection

根据每个圆盘直径选择相应的参数Rat值，每组抗钻阻力值经过平稳卡尔曼滤波器后，成对波峰波谷数量减少，且与圆盘实际年轮数较接近。从323组抗钻阻力值中随机选取20组，试验结果见表2。试验过程中，每个圆盘针刺获取的抗钻阻力值为2组或4组，将对应的2组或4组值滤波后的波峰波谷数取平均值，作为圆盘的滤波算法估计年龄。详细的试验结果和实际年龄对比如图4所示。

图4 滤波算法估计年龄与DECOM自动判定年龄对比Fig.4 Comparisons of age estimation by filtering algorithms and DECOM judgment test

表2 随机选取20组抗钻阻力值序列滤波前后峰谷数对比Tab.2 Comparison of peak-valley numbers before and after filtering for 20 groups of random drilling resistance values

每个圆盘的试验相对误差分布见图5，针刺仪自带软件DECOM自动判定年龄结果误差较大，范围在-25～2年之间，平均误差为-12年；相对误差大多集中在-20%～-60%之间，最小相对误差为-7.69%，最大相对误差为-84.78%，平均相对误差为-40.49%。算法估计年龄误差范围在-6～5年之间，平均误差为-0.25年；相对误差分布大多集中在-10%～10%之间，最小相对误差为0%，最大相对误差为25.69%，平均相对误差为0.75%。

图5 滤波算法估计年龄与DECOM自动判定年龄相对误差分布Fig.5 Relative error distribution of age estimation by filtering algorithms and DECOM judgment test

分别对实际年龄与软件自动判定年龄(第1对)、实际年龄与算法估计年龄(第2对)进行成对数据t-检验。第1对数据检验后t为t1=20.254，给定显著性水平δ=0.05，查表可得t1-δ/2(n-1)=t0.975(9)=2.262 2，由于|t1|>2.262 2，故拒绝原假设，即可认为DECOM软件自动判定树木年龄均值与实际年龄均值之间有显著差异，此时检验的p为2.2e-6。第2对数据检验后t为t2=-0.468 16，由于|t2|<2.262 2，故不能拒绝原假设，即可认为滤波算法估计树木年龄均值与实际年龄均值之间无显著差异，此时检验的p为0.640 7。

4 讨论

通过试验可以看出，针刺仪平稳卡尔曼滤波器理论可以应用于华北落叶松，使得针刺仪成为活立木年龄微损测定的有效工具，且具有以下特点：

1)针刺仪平稳卡尔曼滤波算法是微损的。传统树木年龄的确定方法是查数树木年轮数，需获取树木生长芯或截取树木横截面圆盘(Jeongetal.,2017；Seoetal.,2017)，而针刺仪平稳卡尔曼滤波算法数据是基于针刺仪获取抗钻阻力值，由于针刺后在树木上留下的洞口直径小于1.5 mm，对树木损害很小，因此与传统树木年代学方法确定树木年龄相比，针刺仪平稳卡尔曼滤波算法是微损或准无损的。相比仪器测定分析获取树木年龄的方法，如图像处理法、X-射线法和同位素法等，针刺仪平稳卡尔曼滤波算法使用针刺仪获取数据，由于针刺仪体积小、质量轻，属于便携式设备，克服了以往仪器测定法笨重、成本高、操作繁琐等缺点，便于野外进行试验。

2)针刺仪平稳卡尔曼滤波算法提高了针刺仪测定树木年龄的精度。针刺仪平稳卡尔曼滤波算法通过MATLAB编程实现，将抗钻阻力值作为针刺仪平稳卡尔曼滤波器的输入，根据活立木胸径选择适当的参数Rat值，就可以得出树木的估计年龄，且与实际年龄误差较小。针刺仪自身测定树木年龄的平均相对误差为-40.49%，利用针刺仪平稳卡尔曼滤波算法后，平均相对误差减少至0.75%，同时将算法估计的树木年龄与实际年龄进行成对数据t-检验，二者之间无明显差异，说明算法应用于针刺仪抗钻阻力值序列可以估计华北落叶松年龄，且精度较好。这样就克服了针刺仪自身携带软件判定树木年龄准确率低的缺点，使针刺仪可以成为活立木年龄微损测定的有效工具。

3)针刺仪平稳卡尔曼滤波器理论的创新性。在1个滤波周期内，卡尔曼滤波器存在2个明显的信息更新过程：时间更新过程和观测更新过程(Stepanov，2011)，后验估计值由先验估计值、滤波增益矩阵和先验协方差矩阵确定。针刺仪平稳卡尔曼滤波算法将针刺仪看作一个系统，给出其状态空间模型，以一般的针刺仪卡尔曼滤波理论为基础，推导出简化针刺仪卡尔曼滤波表达式，使得抗钻阻力最优估计值只由前一时刻的后验估计值确定，迭代过程中可省略先验估计值和先验协方差矩阵计算，大大简化了迭代过程，减少了计算工作量，使抗钻阻力值卡尔曼滤波过程更加直观、简洁，克服了一般卡尔曼滤波参数较多、迭代过程复杂的缺点。

本研究根据后验协方差存在上下确界的性质，进一步求出后验协方差矩阵的极限值，将简化针刺仪卡尔曼滤波表达式中的后验协方差矩阵用其极限值表示，从而给出针刺仪平稳卡尔曼滤波器的定义。对针刺仪平稳卡尔曼滤波器的性质分析发现，其等价于一个离散差分方程，这样就将抗钻阻力的后验估计值即最优估计值的求解过程转换成差分方程的求解过程。由于差分方程的解只与参数s有关，而s仅与Rat有关，Rat为Q和R的比值，因此所求抗钻阻力的最优估计值只与Rat有关。通过大量试验发现，Rat值的选取与活立木胸径有关，进而根据径阶大小给出了选择参数依据。

卡尔曼滤波是处理噪声的经典算法之一，本研究基于针刺仪获取的抗钻阻力数据，利用卡尔曼滤波思想，设定极小化性能指标为线性最小方差估计值，将针刺仪看作一个系统，建立系统的状态方程和观测方程，写出一般卡尔曼滤波递推表达式，并对其进行简化得到简化针刺仪卡尔曼滤波器，进一步对简化针刺仪卡尔曼滤波器的表达式进行分析，求出后验协方差的极限值，给出针刺仪平稳卡尔曼滤波器的定义。对于每株活立木，使用针刺仪获取1组抗钻阻力值序列，将其作为针刺仪平稳卡尔曼滤波器的输入，输出为抗钻阻力的最优估计值序列，最优估计值序列的波峰波谷个数确定树木年龄，结果仅仅与参数Rat的取值有关。通过研究样本数据试验结果显示，总是可以找到合适的参数Rat值，使得估计年龄与实际年龄比较接近。

5 结论

本研究在理论上突破了原有卡尔曼滤波的自回归迭代过程，推导出针刺仪平稳卡尔曼滤波器，使得一般针刺仪卡尔曼滤波器的迭代回归过程得到简化，且初始参数设定变得更加简单，只由1个参数确定。通过给出的针刺仪平稳卡尔曼滤波器，可将针刺仪获取的抗钻阻力数据作为输入，得出树木年龄估计值，改进了针刺仪自带DECOM软件识别树木年轮边界准确率低、过于依赖人工经验的缺点，可以作为一种微损估计活立木年龄的有效途径。