基于不同算法的乳化沥青冷再生材料养生性能预测*

杨彦海， 逄海洋， 杨 野

(沈阳建筑大学 交通工程学院， 沈阳 110168)

以往关于养生条件对沥青混合料的研究多是分析了养生条件对性能的影响，没有进行预测分析，而针对沥青混合料的预测模型研究多是针对性能研究，并没有在养生条件和性能之间建立预测模型.本文建立的支持向量机预测模型，以养生条件作为输入参数，分别对混合料40 ℃马歇尔稳定度和15 ℃劈裂强度进行预测研究，同时采用构建的BP神经网络模型进行预测分析，并对各个模型的结果进行对比分析.支持向量机作为一种泛化能力强、收敛速度较快且具有全局优化能力的小样本回归预测模型，已广泛应用于各个领域的预测研究[10-12].本文研究能够很好地揭示养生因素与40 ℃马歇尔稳定度和15 ℃劈裂强度的非线性相关关系.

1 试验设计及方法

1.1 原材料选择

试验采用旧料来自于辽宁省某高速公路的铣刨料，为了使乳化沥青冷再生混合料试件在早期能够达到良好的强度和水稳定性，以及优化原有级配使其满足级配要求，故在试验中加入42.5#普通硅酸盐水泥、粒径为10～20 mm的粗集料和石屑，材料的试验级配为RAP：10～20 mm集料∶石屑∶水泥=73.5∶8∶17∶1.5.所用的乳化沥青的各项基本参数指标为：乳化剂1.4%，稳定剂0.05%，水38.55%，基质沥青62%.成型试件拌和所采用的水为可饮用水，试验中外掺水用量和乳化沥青用量为4.3%和3.0%.

1.2 养生试验

试验级配为73.5%RAP+8%(10～20 mm)集料+17%石屑+1.5%水泥，为了使样本数量充足，每组试验设置相同条件的平行试件，并取均值作为代表值，数据如表1所示.

2 模型介绍

支持向量机是一种基于统计分析理论发展而来较为先进的智能算法，已经在许多领域得到成功应用[13-14].支持向量机理论首先以学习有限个样本数据为基本脉络，再建立能够反映自变量与因变量非线性函数的关系，最后构造回归估计函数进行预测[15-17].利用Mapminmax函数进行试验数据的归一化处理，采用K-CV法优化惩罚参数c和径向基核参数g，从而搜寻到网络性能最佳时的c和g数值，借助最佳参数c和g训练支持向量机预测模型，实现对数据的预测.

遗传算法是由Holland教授创立的，其理论依据是“优胜劣汰，适者生存”.通过设置种群数量进行不断地种群选择、交叉和变异，不断提升种群的质量[17].

BP神经网络是一种通过误差逆向传递进行不断训练的多层前馈神经网络.借助遗传算法的全局搜寻最优解的能力来对神经网络进行优化，能够有效增大BP神经网络预测精度，其网络拓扑结构如图1所示.

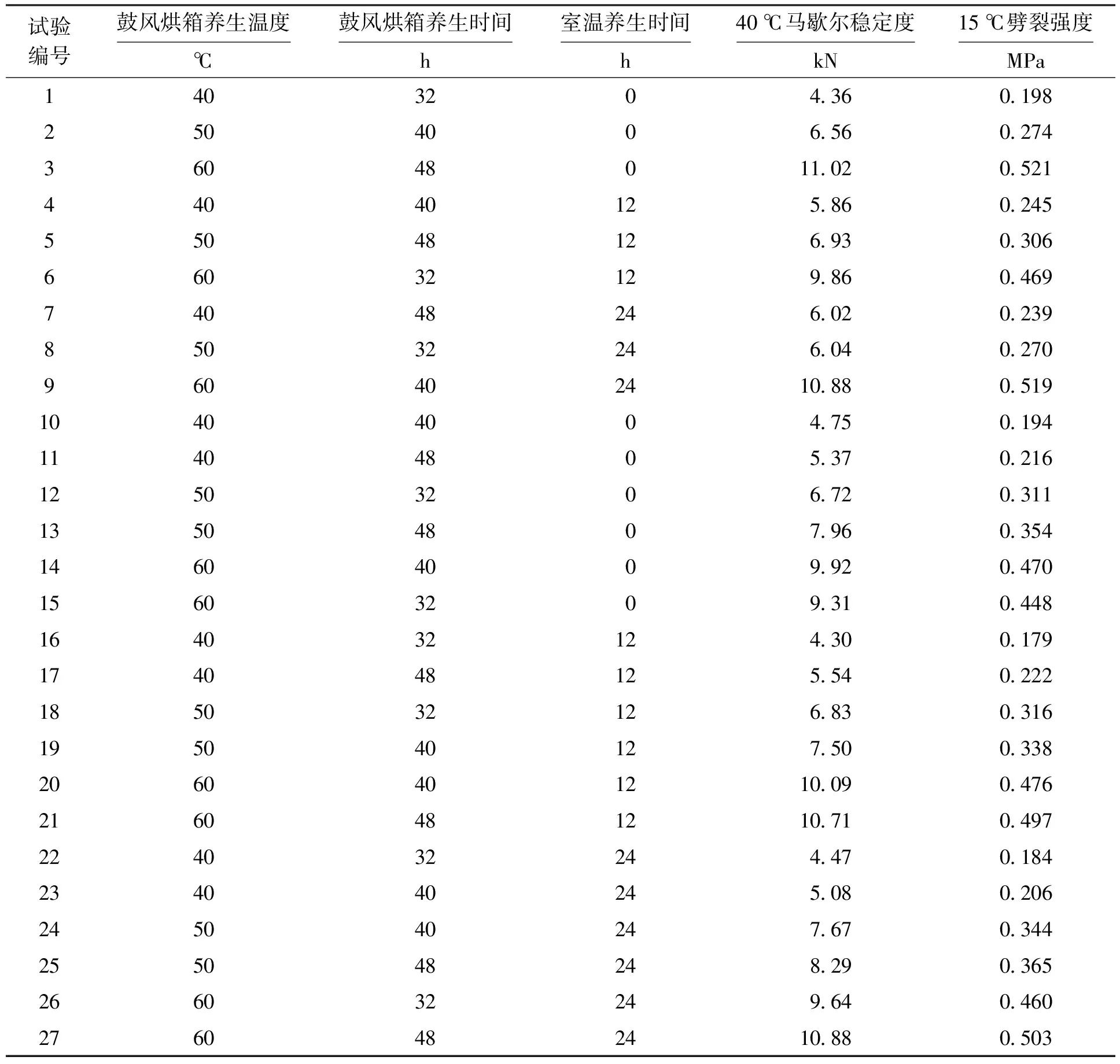
表1 试验数据Tab.1 Test data

图1 BP神经网络拓扑结构Fig.1 Topological structure of BP neural network

图1中，Xi为输入值，Y为输出值，w为网络权值.BP神经网络分为训练和预测两个部分，首先输入样本进行训练学习，当经过大量的学习之后，该网络对信息的挖掘识别能力会变得更为准确，进而对未知样本的预测就更为准确[18].遗传优化BP神经网络流程如图2所示.

3 模型建立与求解

3.1 K-CV优化支持向量机预测模型建立

选取试验鼓风烘箱养生温度、鼓风烘箱养生时间和室温养生时间作为输入参数，分别选取40 ℃马歇尔稳定度和15 ℃劈裂强度作为输出参数.利用上述Mapminmax函数，采用K-CV优化支持向量机模型输出结果，即相关性(R)、均方误差(MSE)和误差率来评价模型准确性，算法流程如图3所示.

针对40 ℃马歇尔稳定度的K-CV法参数选择结果等高线图如图4所示，参数选择结果3D视图如图5所示，预测结果如图6所示，误差率(预测值和真实值之差除以真实值)如图7所示.

图2 优化流程Fig.2 Flow chart of optimization

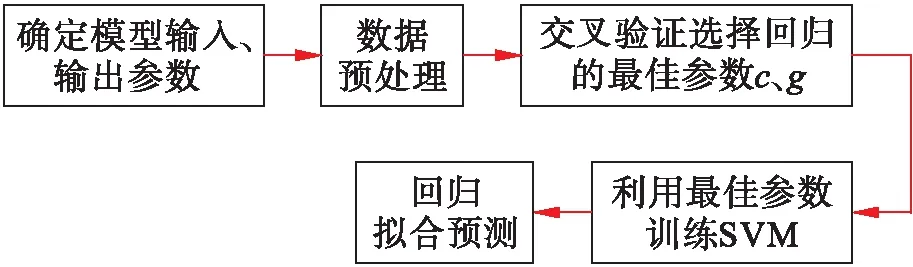
图3 算法流程Fig.3 Flow chart of algorithm

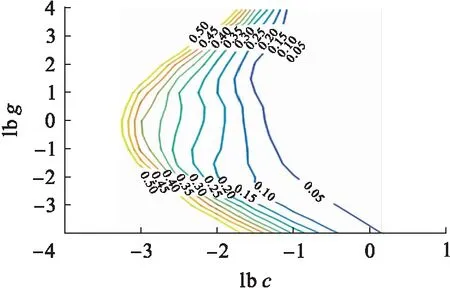
图4 40 ℃马歇尔稳定度参数选择等高线图Fig.4 Contour of parameter selection with 40 ℃ Marshall stability

由图4～5可知，得到的最优参数为c=5.656 9，g=0.062 5.通过图6～7分析得出，40 ℃马歇尔稳定度预测值与真实值拟合效果良好，最大误差率小于6%，误差率集中在2%以内，表明回归预测结果准确.其中均方误差MSE=0.000 300 222，相关系数R=99.730 9%，表明该模型具有较好的数据拟合效果，并且预测误差小.

针对15 ℃劈裂强度的K-CV法参数选择结果等高线图如图8所示，参数选择结果3D视图如图9所示，预测结果如图10所示，误差率如图11所示.

图5 40 ℃马歇尔稳定度参数选择结果3D视图Fig.5 3D view diagram of parameter selection results with 40 ℃ Marshall stability

图6 SVM 40 ℃马歇尔稳定度预测结果Fig.6 Prediction results of SVM with 40 ℃ Marshall stability

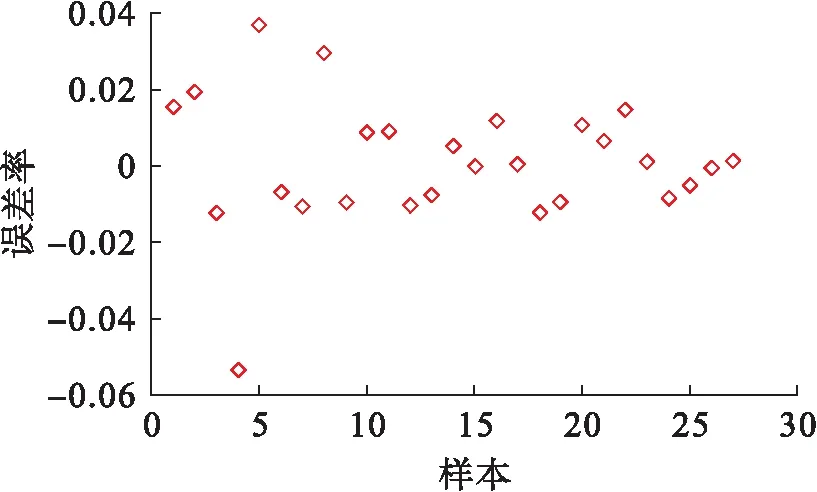
图7 SVM 40 ℃马歇尔稳定度误差率Fig.7 Error rate of SVM with 40 ℃ Marshall stability

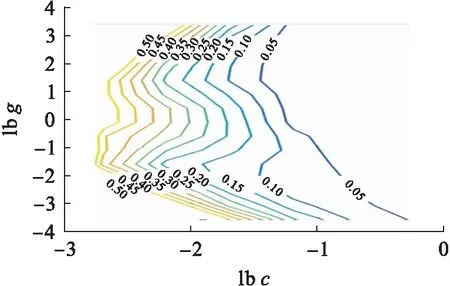
图8 15 ℃劈裂强度参数选择等高线图Fig.8 Contour of parameter selection with 15 ℃ splitting strength

图9 15 ℃劈裂强度参数选择结果3D视图Fig.9 3D view diagram of parameter selection results with 15 ℃ splitting strength

图10 SVM 15 ℃劈裂强度预测结果Fig.10 Prediction results of SVM with 15 ℃ splitting strength

图11 SVM 15 ℃劈裂强度误差率Fig.11 Error rate of SVM with 15 ℃ splitting strength

由图8～9可知，得到的最优参数为c=4.924 6，g=0.082 469.通过图10～11分析得出，15 ℃劈裂强度预测值与真实值拟合效果良好，最大误差率小于6%，误差率集中在2%以内，回归预测结果准确，其中均方误差MSE=0.000 210 547，相关系数R=99.828 1%，表明该模型具有较好的数据拟合效果，并且预测误差小.

3.2 GA优化BP神经网络预测模型建立

确定输入参数为试验鼓风烘箱养生温度、鼓风烘箱养生时间和室温养生时间，选取40 ℃马歇尔稳定度作为输出参数.根据图2优化神经网络流程图，首先采用遗传算法对权值阈值进行优化，其中种群规模为10，进化代数为100次，交叉和变异概率分别为0.4和0.2，其优化的适应度曲线变化如图12所示.

图12 40 ℃马歇尔稳定度适应度曲线Fig.12 Fitness curve with 40 ℃ Marshall stability

由图12可知，经过15次迭代后，个体适应度基本稳定，表明该模型的稳定性较高，对于40 ℃马歇尔稳定度的预测结果如图13所示，预测误差如图14所示，模型的拟合优度图如图15所示.

图13 40 ℃马歇尔稳定度预测结果Fig.13 Prediction results with 40 ℃ Marshall stability

图14 40 ℃马歇尔稳定度误差率Fig.14 Error rate with 40 ℃ Marshall stability

通过对图13～14的分析可知，该模型的预测误差率集中在0～5%之间，最大误差率小于20%，该模型的预测较为准确.

通过对图15进行分析，该模型的总体拟合优度R=0.979 08，拟合效果良好，模型的适用性较强.确定输入参数为试验鼓风烘箱养生温度、鼓风烘箱养生时间和室温养生时间，选取15 ℃劈裂强度作为输出参数，其优化的适应度曲线变化如图16所示.

图15 40 ℃马歇尔稳定度拟合优度图Fig.15 Fitted goodness with 40 ℃ Marshall stability

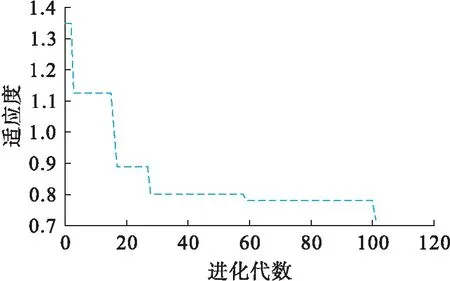
图16 15 ℃劈裂强度适应度曲线Fig.16 Fitness curve with 15 ℃ splitting strength

通过对图16分析得出，在经过约25次迭代后，个体适应度逐渐趋于平稳，表明该模型的稳定性较高，对15 ℃劈裂强度的预测结果如图17所示，预测误差如图18所示，模型的拟合优度图如图19所示.

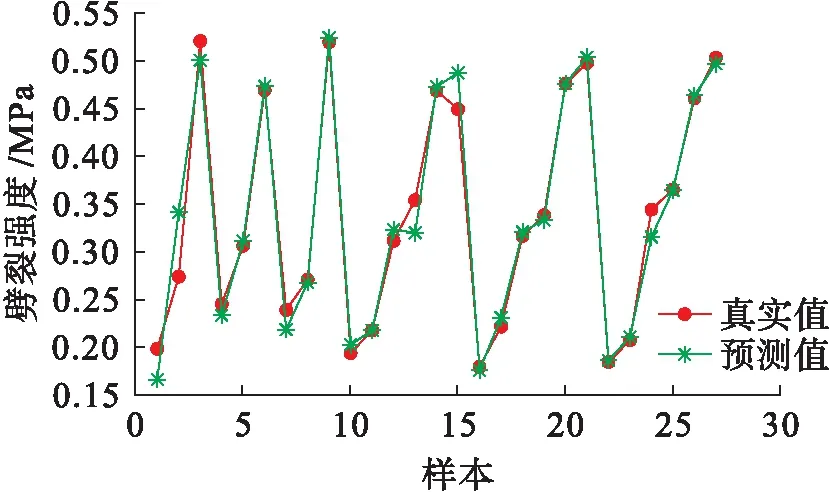
图17 15 ℃劈裂强度预测结果Fig.17 Prediction results with 15 ℃ splitting strength

图18 15 ℃劈裂强度误差率Fig.18 Error rate with 15 ℃ splitting strength

通过对图17～18进行分析可知，该模型的预测误差率集中在0～5%之间，最大误差率集中在20%以内，该模型的预测较为准确.

通过对图19分析可知，该模型的总体拟合优度R=0.986 04，拟合效果良好，模型的适用性较强.

4 结 论

本文通过分析得出以下结论：

1) 基于不同养生条件下40 ℃马歇尔稳定度和15 ℃劈裂强度的相关试验数据，构建的支持向量机模型能够准确预测40 ℃马歇尔稳定度，其均方误差MSE=0.000 300 222，拟合优度R=99.730 9%，最大误差率小于6%.对15 ℃劈裂强度也能进行准确预测，其均方误差MSE=0.000 210 547，拟合优度R=99.828 1%，最大误差率小于6%，该模型具有较好的数据拟合效果，并且预测误差小.

2) 构建的BP神经网络模型能够较为准确地预测40 ℃马歇尔稳定度，其预测误差多数在0～5%之间，总体拟合优度达到0.979 08.对15 ℃劈裂强度也能进行较为准确地预测，预测误差多数在0～5%之间，总体拟合优度达到0.986 04，模型具有较好的数据拟合效果，神经网络模型的预测误差总体大于支持向量机模型的预测误差，但也能进行较为准确地预测.

图19 15 ℃劈裂强度拟合优度图Fig.19 Fitted goodness with 15 ℃ splitting strength

3) 相较两种模型，支持向量机的预测效果更能进行准确地预测，更适用于本文研究.