基于DTW-LSTM的短期楼宇电力负荷预测方法*

张明理， 张明慧， 王 勇， 武志锴， 满林坤

(1. 东北大学 软件学院， 沈阳 110169； 2. 国网辽宁省电力有限公司 a. 经济技术研究院， b. 财务资产部， 沈阳 110015)

在增量配电网投资管理中，因为楼宇用电行为对大型园区能耗影响较大，故针对楼宇电力负荷预测具有较为重要意义[1].鉴于电能难以存储的特性，电企的生产能力应该能够根据实际用电进行动态调整.楼宇用电作为电能主要用途之一，对楼宇短期的电力负荷精准预测既可以降低电能的损耗，又能保证用电环境的安全与稳定.

智能电网是未来电网发展的必然趋势[2]，智能电网的重要组成部分是安装在各个楼宇中的智能电表，其可定期发送和接收楼宇与供电商之间的用电量信息，且随着数据存储和处理器功能的增强，可以将获得的大量楼宇用电数据以时间序列的形式进行存储，对数据进行处理后，即可预测未来的用电情况.

在过去的几十年中，学者们提出的众多统计和人工智能方法应用于短期电力负荷预测.李泽文等[3]利用时间序列分析和加权最小二乘法建立ARMA模型，实现短期的负荷预测，但最终预测精度仍有较大的提升空间.许言路等[4]发现，随着神经网络的兴起，卷积神经网络(CNN)在多个方面均表现出卓越的贡献，在具有时间序列特征的电力负荷预测方面也有优越表现.余登武等[5]提出利用深度卷积神经网络(DCNN)模型来预测加拿大维多利亚市一周中每一天的用电负荷，但随着网络深度的增加，预测精度会趋于饱和甚至下降.此外，循环神经网络(RNN)使用也较为普遍，其中最为著名的是长短期记忆(LSTM)循环神经网络.李鹏辉等[6]提出一种基于LSTM的短期高压负荷回归预测方法，通过引入自循环权重，各单元彼此循环连接，动态化地改变积累时间尺度，使其具有长短期记忆并表现出优异的性能.

仅使用统计方法或人工智能方法进行短期负荷预测精度受限，故结合聚类算法对用电行为进行分析的想法被提出.艾欣等[7]应用K-Means、K-Medoid和SOM聚类算法，根据家庭一天的用电模式划分为簇，并产生能代表家庭内常见用电模式的曲线；赵凯等[8]将SOM与K-Means算法相结合应用于工业建筑能耗模式分析，并成功识别出不同的能耗及相关行为模式；史静等[9]根据用户消费模式的相似性，利用周期性分析和K-Means聚类算法将用户进行分组.然而现在大多数传统聚类算法会导致簇数过多，其中每个用电曲线可能与多个簇有关，用电曲线无法确定固定的模式.针对上述问题，本文的贡献如下：

1) 采用一种基于形状的动态时间规整(DTW)聚类算法对楼宇日用电曲线进行聚类，并对聚类结果进行编码.

2) 利用马尔科夫链模型，根据楼宇过去10天用电曲线所属簇的编码对未来一天的用电曲线编码进行预测，该步骤的目的是预测出未来一天的用电曲线原型.

3) 以编码为特征，通过LSTM网络，根据楼宇历史用电数据对楼宇未来的短期负荷进行预测.

4) 将DTW-LSTM短期负荷预测模型与LSTM模型进行对比实验，由此分析DTW聚类对预测精度的提升效果.其次针对传统的短期负荷预测SVR模型做出对比实验，从而说明本文所提出模型最终的效果.

1 DTW-LSTM模型

1.1 DTW聚类算法

对于楼宇的用电曲线，传统聚类算法采用的是基于欧式距离的度量，其只能对同一时刻的用电数据进行相似评估.楼宇的用电曲线可能在两个不同时间段具有相似的用电行为，若继续采用基于欧式距离度量的聚类算法，则可能最终的聚类效果较差且具有较多的簇数目[10].

DTW算法专门用于处理衡量时间序列相似度问题，通过在时间轴上的非线性拉伸或收缩进行两条用电曲线的形状匹配.算法具体描述如下：比较两个长度为N的时间序列X和Y，首先需要定义一条规整路径p=(p1，p2，…，pL)，其中pi=(ni，mi)∈[1∶N]×[1∶N](1≤i≤L).规整路径需要满足以下条件：

1) 边界条件.其中p1=(1，1)，并且pL=(N，N).

2) 单调性.路径上的每个点必须随着时间单调进行变化，故ni和mi满足n1≤ni≤nL，m1≤mi≤mL.

3) 连续性.对于路径上一点pi=(ni，mi)及下一个点pi+1=(ni+1，mi+1)满足ni+1-ni≤1，且mi+1-mi≤1.

满足上述条件后，根据d(xn，ym)=(xn-ym)2，可以计算时间序列X与Y之间的规整路径总代价为

(1)

最优规整路径p*是所有可能的规整路径中，总代价最小的一条.序列X与Y之间的DTW距离即为最优规整路径总代价，定义为

dDTW(X，Y)=cp*(X，Y)

(2)

p*=arg mincp(X，Y)

(3)

为了计算两条负荷曲线的DTW距离，找到最优的规整路径，本文利用动态规划思想求解.首先计算时间序列X与Y中每两个点之间的距离，并利用一个代价矩阵C保存.最优规整路径的总代价可以递归计算，递归公式为

dDTW(xi，yj)=d(xi，yj)+min(dDTW(xi-1，yj)，

dDTW(xi，yj-1)，dDTW(xi-1，yj-1))

(4)

最终dDTW(xN，yN)即为最佳规整路径的总代价.给定楼宇负荷曲线序列X，聚类数目K，每个簇的原型设为uk.基于DTW的聚类算法目的是找到K个簇的DTW距离之和最小，即

(5)

因此，通过DTW算法进行聚类得到的每个簇的用电曲线中相同时刻的用电情况可能差异较大，但整体用电规律是相似的.

1.2 马尔科夫链模型

马尔科夫链过程是以系统状态转移规律作为基础，研究和分析事物的发展趋势，从而推导出事物未来最有可能出现的状态[11].

选取历史编码作为划分系统状态的根据，设编码序列共包含r种状态，记为s1，s2，…，sr.当聚类数目为K类时，其中的某个状态si的取值范围为[0，K-1].历史的编码数据从si状态经过n步转移到sj状态的概率为

Pij(n)=Mij(n)/Mi

(6)

式中：Mij(n)为编码序列中由si状态转移到sj状态的次数；Mi为编码序列处于si状态的总次数.

基于式(6)可以求出马尔科夫链n步的状态转移矩阵为

(7)

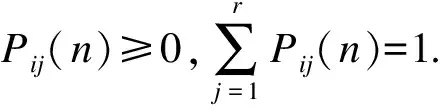
计算出转移矩阵，则要预测r+1步的状态.以第r步的状态sr为依据，从状态转移矩阵中找到状态sr转移的最大概率，即max(Prl(n))，其中l=1，2，…，r，最终sl状态则为r+1步可能性最大的状态.

1.3 长短期记忆网络

Hochreiter等[12]最早提出了LSTM神经网络，其对RNN做出了改进.RNN是用于处理序列数据的神经网络，随着历史信息和当前预测信息距离的增大，其丧失了从过去学习信息的能力，即梯度消失问题.而LSTM神经网络能够解决RNN的梯度消失问题，LSTM神经网络标准结构如图1所示.

LSTM神经网络之所以能够解决梯度消失问题，主要是引入了一个Cell处理器.在Cell中主要包含三扇门，分别为遗忘门、输入门及输出门[13-14].

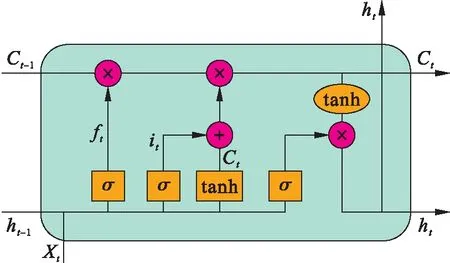
图1 LSTM网络结构Fig.1 LSTM network structure

遗忘门用于决定上一阶段有多少信息可以传递到当前状态.若输出为0，则丢弃上一阶段的全部信息；若输出为1，则保留上一阶段的信息，其筛选表达式为

ft=σ(Wf[ht-1，Xt]+bf)

(8)

式中：σ为sigmoid激活函数；Wf为遗忘门当前的输入Xt与前一时刻输出ht-1相乘的权重；bf为偏置.

输入门用来决定有多少当前输入信息可以加入记忆单元.通过sigmoid层决定更新值，通过tanh层生成当前新的记忆单元候选状态，即

(9)

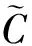
输出门主要决定模型的输出，其利用sigmoid函数得到初始输出，再利用tanh函数将值缩放到(-1，1)，将两者相乘得到输出公式为

ht=ottanhCt

(10)

ot=σ(W0[ht-1，Xt]+b0)

(11)

函数sigmoid是不考虑之前学到的信息输出，函数tanh则是对之前学到的信息进行压缩，将两者结合即为LSTM的思想.

1.4 整体模型

本文提出的整体网络结构如图2所示.模型主要包含3个部分，第1部分是对楼宇日用电曲线进行聚类，得到K簇并对簇编码(0～K-1)；第2部分利用马尔科夫链模型预测楼宇的用电曲线编码，每个楼宇利用r天的用电编码预测第r+1天的用电编码，目的是为了得到r+1天的用电曲线原型；第3部分是对楼宇的短期负荷进行预测，将马尔科夫链预测的用电编码作为一个特征，结合历史负荷数据，利用LSTM进行短期的负荷预测.

2 实验过程

2.1 实验配置

本案例研究选择芝加哥8个楼宇2014年6月至9月工作日的用电情况，共计696条日用电曲线，用电数据获取频率为每小时一次.研究中涉及的所有实验均基于python3.7编译环境下，神经网络模型均基于TensorFlow开发的Keras.实验涉及的模型超参数如表1～2所示.在进行深度模型实验时，对数据进行分割，其中60%的数据作为训练集，20%的数据作为验证集，其余的20%作为测试集.

图2 整体网络结构Fig.2 Overall network structure

表1 SVR模型超参数Tab.1 SVR model hyper-parameters

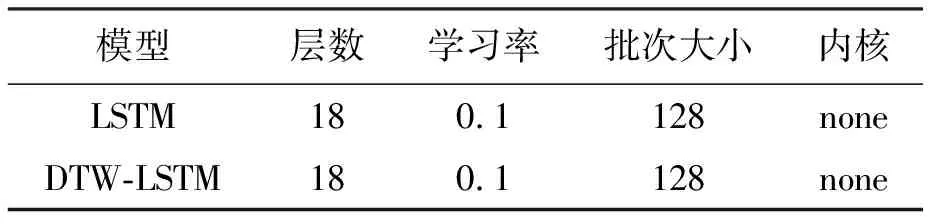
表2 深度模型超参数Tab.2 Depth model hyper-parameters

2.2 聚类实验

2.2.1 聚类评价标准

为了评价聚类的效果，本文利用3个性能指标来进行衡量：

1) 各簇中的用电曲线与簇中心的距离之和记作WC，该指标可以评价簇的紧凑性.

2) 各簇心之间的距离之和记作WB，该指标可以评价簇之间的差异性，计算表达式为

(12)

3) WC与WB的比值记作WCBCR，该指标可以评价两者变化的比率.一个好的聚类结果，应具有较小的WC值和WCBCR值，以及较大的WB值.

2.2.2 聚类结果

对于8个楼宇的日用电曲线数据，实验聚类数目为5～65簇.图3记录了不同聚类数目的WCBCR评价指标.

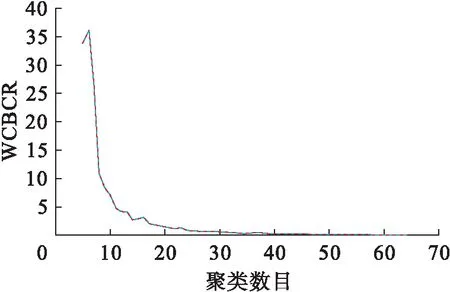
图3 WCBCR指标Fig.3 WCBCR indicator

随着聚类数目增多，簇之间的距离之和变大，故WB的值增大；每个簇中曲线越来越紧凑，故WC的值减小.综合上述两点，WCBCR的值随着聚类数目增加逐渐减小.但在聚类数目11之前下降较快，而在聚类数目11之后下降较慢，根据拐点法选择聚类数目为11最佳.图4为最终的聚类结果，并对每个簇进行编码(0～10).

2.2.3 编码预测

对于编码的预测，本文基于楼宇中每10天的编码，并利用马尔科夫链模型预测第11天的编码.

对于每个楼宇，编码预测正确率如表3所示.从表3中可以得到编码预测平均正确率为92.19%，这为下一步负荷预测奠定了良好的基础.

2.3 负荷预测实验

2.3.1 预测结果评估指标

对实验预测结果的评估指标使用绝对百分比误差(MAPE)、平均绝对误差(MAE)以及均方根误差(RMSE)，其具体计算表达式为

(13)

(14)

(15)

式中：Zip为预测值；Zit为真实值.

2.3.2 负荷预测结果

1) LSTM与DTW-LSTM比较.该实验主要是为了说明DTW聚类算法对预测结果的提升，表4分别给出了两个模型的各参数对比情况.

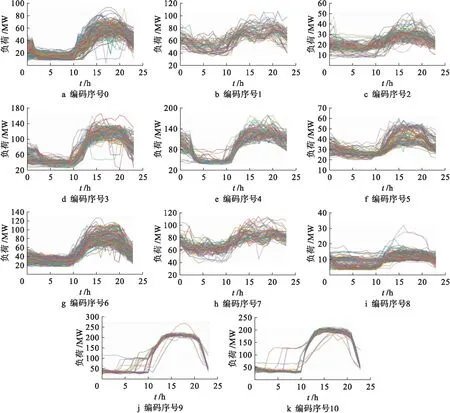
图4 11簇聚类结果Fig.4 Clustering results of 11 clusters

表3 编码预测正确率Tab.3 Coding forecasting accuracy

从表4中可以看出，DTW-LSTM模型对于各个楼宇的预测精度均有所提升.以MAPE指标为例，提升幅度最大值为1.325 2%，最小提升幅度为0.38%，平均提升幅度为0.861 3%.通过分析发现，8号楼中的日用电曲线的聚类结果较为分散，故编码对负荷预测的影响较大；而1号楼中的日用电曲线聚类结果几乎为同一个簇，编码对负荷产生的影响较小，符合最终的结果.

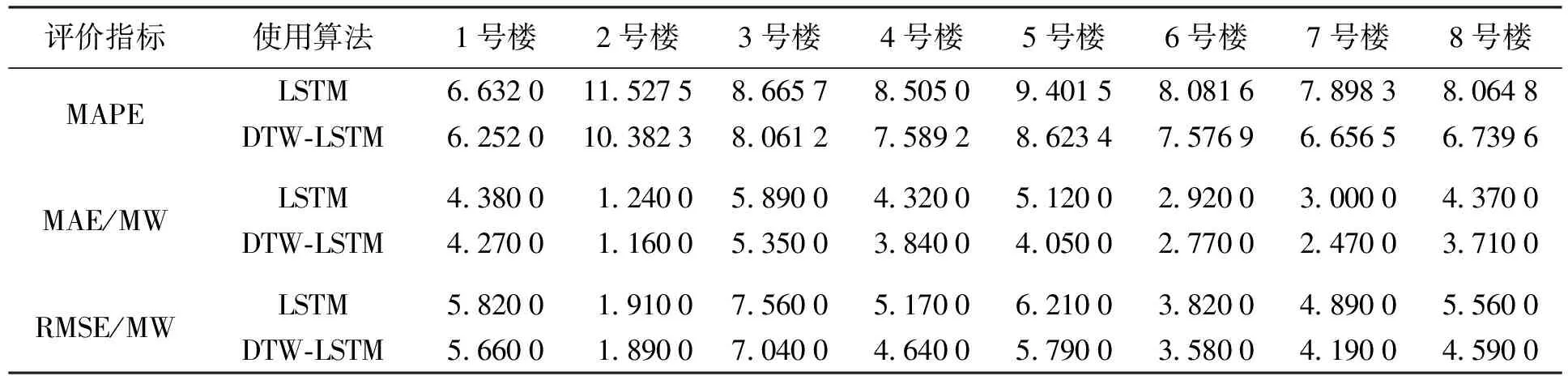
表4 MAPE、MAE和RMSE指标Tab.4 MAPE，MAE and RMSE indicators

综上所述，DTW聚类用电原型的预测对于最终的负荷预测精度提升是有帮助的，且该模型对楼宇的负荷预测具有普适性.

2) DTW-LSTM与SVR比较.为了证明DTW-LSTM模型相对于传统负荷预测模型的性能提升，本文选择SVR模型进行精度对比，对比结果如表5所示.

由表5中可以发现，DTW-LSTM模型在各性能指标方面均优于SVR模型，MAPE指标平均降低1.703%，MAE指标平均降低1.056 MW，RMSE指标平均降低1.06 MW，且模型具有泛化能力，对所有的楼宇具有普适性.因此在实际的应用中，DTW-LSTM模型完全能够胜任楼宇短期的负荷预测.

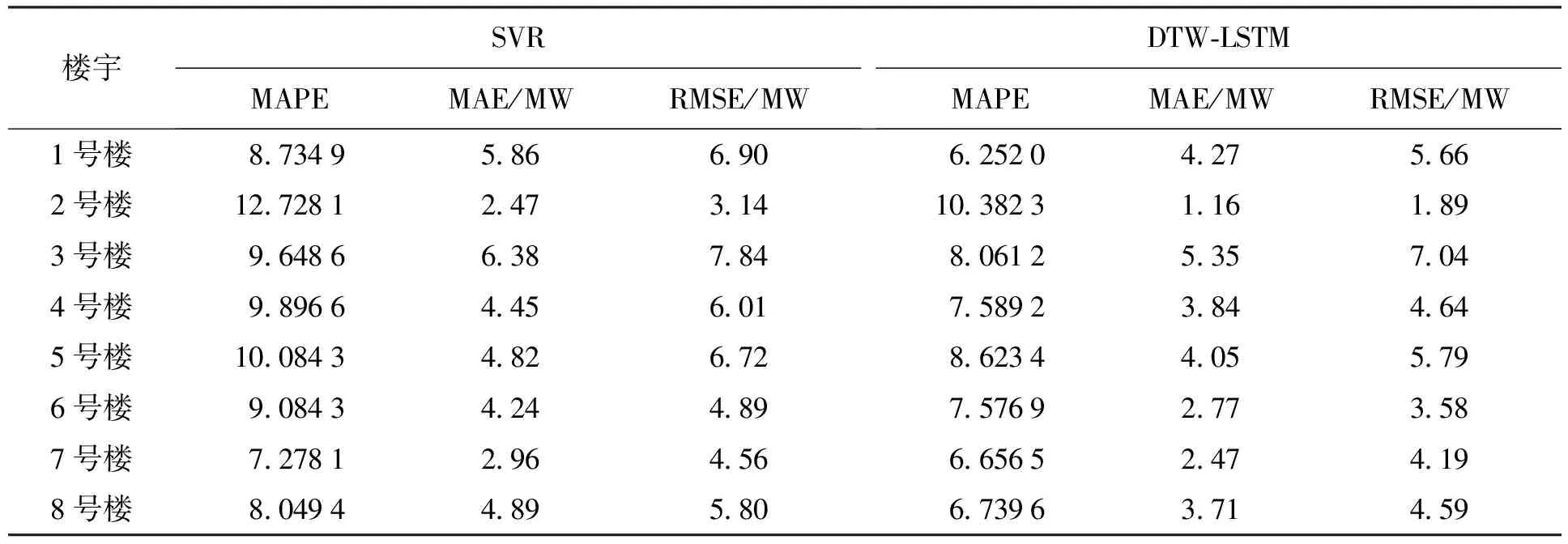
表5 性能对比结果Tab.5 Performance comparison results

3 结 论

本研究提出了DTW-LSTM短期负荷预测模型.首先与LSTM神经网络模型进行性能对比，说明DTW聚类后预测未来的用电原型对精度的提升效果；其次与SVR模型进行系统地比较，分析其模型对比传统算法提高的效果.实验表明，DTW-LSTM短期负荷预测模型取得了较好的效果.

综上所述，DTW-LSTM模型在负荷预测精度上有所提高，且该模型对楼宇具有普适性.但在此基础上，仍可继续研究，例如将日用电曲线进行划分，将划分结果进行DTW聚类，这样的编码会精确到以小时为单位，最终负荷预测精度仍将会有所提高.