基于线上研讨的三角形中位线定理课例研究

【摘 要】在后疫情时代，基于专业学习共同体的线上研讨成了重要的教研方式。研究者以三角形中位线定理为例，整理了HPM课例线上研讨和线下实施的过程，呈现了研究方法、实施流程、研究结果、教研规律等，为初中教师线上教研和课堂教学提供参考。

【关键词】线上研讨;三角形中位线定理;专业学习共同体;课例研究

【作者简介】司睿，华东师范大学教师教育学院在读硕士研究生，主要从事数学史与数学教育研究。

随着HPM专业学习共同体的扩大和课例研究的深入开展，越来越多的HPM课例应运而生，但由于历史研究、教学设计、学术研讨、学生基础等多方面的原因，这些课例都有待进一步完善的空间。以三角形中位线定理为例，已有课例[1]11-15的不完善之处主要有以下两个方面：一是学生在课堂上探究三角形中位线定理的证明时，未能再现历史上所有的方法;二是学生在做出证明时，教师未能通过古今对照及时进行评价，从而失去了落实学科德育的机会。

在后疫情时代，HPM工作室课例研究的“研讨与设计”环节，从线下转到了线上，线上交流平台的多样化与时间的灵活性使得课例的研讨与交流更加便捷。通过网络教研平台，高校研究人员汇报相关主题的历史，总结已有的教学设计。执教者汇报其初步的教学设计，然后HPM工作室成员展开深入研讨。执教者根据研讨结果，对教学设计进行改进后，选择一个或多个班级进行试讲，再根据试讲的效果，对教学设计做出进一步的完善，最后付诸实践。本文以三角形中位线定理为例，呈现基于线上研讨的课例研究过程。

一、历史材料及其应用

公元前1700年左右，古巴比伦泥版书记载了许多三角形土地分割问题，其中包括三角形中位线的问题。

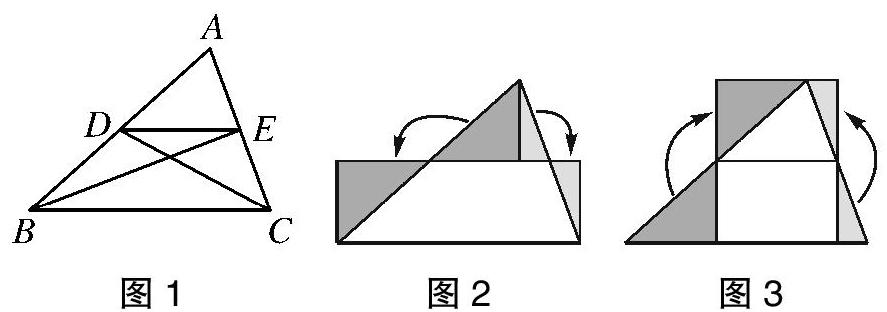
欧几里得在《几何原本》中利用面积法证明了更一般的定理（命题VI.2）：“将三角形两腰分割成成比例的线段，则分点连线段平行于三角形的底边。”[2]如图1，在中位线的特殊情形中，因为△BDE和△CED面积相等，故DEBC;又因为△BCE的面积是△BDE的两倍，故BC = 2DE。

中国汉代数学典籍《九章算术》“方田”章中记载了求三角形土地面积的问题：“今有圭田廣十二步，正从二十一步。问：为田几何？”术曰：“半广以乘正从。”[3]三国时期数学家刘徽利用出入相补法，将三角形转化为矩形，由此推导出三角形的面积公式，如图2和图3所示。[4]同样的方法可用于三角形中位线性质定理的证明。

18—20世纪的西方几何教科书采用多种方法证明三角形中位线定理。法国数学家勒让德（A.M.Legendre）在《几何基础》中采用了反证法;苏格兰数学家莱斯利（J.Leslie）在《几何和平面三角学基础》中沿用了欧氏面积法;美国数学家菲利普（Phillips）在《几何基础》中利用平行线等分线段定理，采用同一法来证明;美国数学家维纳布尔（Venable）在《几何基础》中采用了平行四边形法进行证明。在19 世纪末20 世纪初的几何教科书中，大多数采用图4所示的平行四边形法来证明三角形中位线定理。我国现行初中教科书大多数采用此法。

法国数学家瓦里尼翁（P.Varignon）利用三角形中位线定理，发现顺次连接四边形各边中点所得的四边形是平行四边形，且面积是原四边形的一半，后人将中点四边形称为瓦里尼翁四边形。

从古巴比伦泥版书上记载的三角形土地分割问题，到不同国家和地域的数学家的不同证明方法，其凝结了丰富的数学思想，呈现了多元的数学文化。本节课设计探究活动，再现三角形中位线定理的发现过程与不同的证明方法，通过古今对照，实现数学史的多元教育价值。

二、基于线上研讨的课例研究

执教者研读三角形中位线定理的历史素材以及已有的课例，并和高校研究者借助在线网络平台进行简短的沟通后，提出了自己的困惑以及创新的难点，接着根据自己的思考和经验完成教学设计（Ⅰ），之后HPM专业学习共同体利用腾讯会议平台，就教学设计进行深入研讨。

1.线上研讨

在第一次线上研讨会上，高校研究者首先就三角形中位线定理这一主题，做了史料、课程标准和教材的分析，以及已有教学设计的综述。执教者汇报了教学设计（Ⅰ）的设计过程，并提出自己的困惑。

执教者将本节课定位为一节探究课，通过引导学生对三角形中位线定理的不同证明方法进行探究，形成古今对照。教学目标如下。

（1）理解三角形中位线概念，经历三角形中位线概念的形成过程，体会从特殊到一般的数学思想。

（2）经历三角形中位线定理的探索过程，体会观察、归纳、推理、应用的数学研究过程，感受严谨、务实的科学态度。

（3）了解历史上三角形中位线的证明方法，感悟其历史文化内涵和古人的探究精神，体会几何学的魅力。

本节课的教学重点是三角形中位线定理的证明，教学难点是证明方法的探究。

教学过程由活动引入、定理探究、新知应用、课堂小结和布置作业五个环节构成，具体见表1。

之后，大家对教学设计（Ⅰ）进行探讨：关于活动引入环节，距离测量的情境已经被人们广泛采用;已有的HPM课例的三角形土地分割情境，是根据古巴比伦泥版书上的土地分割问题改编的，教师从学生的分割方案出发，自然引出三角形中位线概念[1]11-15。为了有所创新，执教者设计了“三角形的内接三角形”问题。高校研究者认为该问题并没有建立在学生的生活经验基础上，不符合三角形中位线产生的历史动因，显得不够自然。关于活动引入环节，高校研究者提出两个建议：（1）通过设计三角形瓷砖的粘贴方案，引导学生发现三角形中位线概念和性质再设计证明;（2）通过推导三角形面积公式引入，学生可能会采用分割的方案，利用有关方案，即可自然引出三角形中位线概念。

关于定理探究环节，高校研究者提出两个建议：（1）总结证明方法所蕴含的转化思想——面面关系与线线关系的转化;（2）从特殊到一般建立不同证明方法之间的联系。关于新知应用环节，大家认为，本节课的重点在于三角形中位线定理的探究，中点四边形对于学生来说较难，不宜喧宾夺主。关于课堂小结环节，高校研究者建议应从知识升华到数学思想的高度。

2.第一次试讲

集体在线研讨后，高校研究者和执教者线上讨论，选取适当的史料，制作按照时间顺序呈现三角形中位线定理发展的微视频，以便更好地进行古今对照。根据高校研究者整理的在线研讨的反馈，执教者对教学设计（Ⅰ）做了改进，形成教学设计（Ⅱ），见表2。

执教者根据教学设计（Ⅱ）进行了第一次试讲。学生在课堂上分别将三角形转化为平行四边形、矩形和梯形，与历史上数学家的证明方法一致，达成了教师的预期目标，整个课堂氛围良好，学生纷纷展示自己的证明。关于中点四边形的面积问题（如图7），一名学生连接四边形对角线AC，利用三角形全等来证明。在最后的课堂小结环节，除了对知识内容进行归纳总结，一名学生还上升到了数学思想的高度。他指出，证明方法的背后是转化，构造矩形的方法是构造平行四边形方法的特例，构造两组全等三角形，其实是构造一组三角形全等的特例，转化为梯形的方法是研究三角形的面积在等高的情况下底边之间的关系。

3.第二次试讲

第一次试讲基本达到了预期的教学效果。在仔细阅读教科书和史料后，执教者发现教科书上的例题和中点四边形有关，于是根据学生的实际情况對新知应用环节的例2做了一些改动，形成教学设计（Ⅲ）：首先，设计一个图形（如图8），其中点C是△ABD内任意一点，点E、F、G 、H分别是BC、DC、AD、AB的中点，求证四边形EFGH是平行四边形;接着，完成证明后，去掉线段BD，得到凹四边形ABCD（如图9），从而引出中点四边形;然后，将点C向下拉，得到一个凸四边形（如图10），让学生继续探究结论是否成立，体会数学中的 “变与不变”;最后，教师介绍法国数学家瓦里尼翁的发现，并让学生证明中点四边形的性质。

按照教学设计（Ⅲ），执教者进行了第二次试讲，但是课堂上并未出现欧几里得的面积法。

4.第三次试讲

第二次试讲的效果并不理想，执教者做了以下反思：其一，三角形面积公式的探究是以课前学习单的形式布置的，课上直接展示，既没有打开学生的思路，也没能调动学生探究的积极性，以致在探究过程中学生并没有完全呈现历史上的不同证明方法;其二，由于借班上课，教师不了解学情，因此对学生引导不够。于是执教者通过腾讯会议平台与高校研究者一起进行了第二次线上研讨，对教学设计（Ⅲ）进行修改，形成教学设计（Ⅳ），见表3。

设计剪纸活动的原因是，执教者在前两次试讲时发现，有的学生在利用中位线分割三角形后证明中位线定理会花费较多时间，且违背了引入环节的初衷。剪纸活动既可以规避上述问题，也可以为后面的定理探究环节构建不同的证明方法做铺垫。修改口答练习题的原因是，执教者认为原题目对于学生来说过于简单，不直接给出三角形更具开放性。

执教者按照教学设计（Ⅳ）进行了第三次试讲。在活动引入环节，执教者引导小组成员分工合作，分别负责画图、剪纸和展示。学生依次呈现了平行四边形法、刘徽的方法。在利用欧几里得面积法时，学生只得到中位线与底边的位置关系，未能证明出大小关系。

三、最终教学设计

从选题到初步设计，从第一次线上研讨到每次试讲后与高校研究者的交流，前后历经将近一个月的时间。在经历教学设计的三改三试后，执教者第四次实施课堂教学，取得了较理想的效果。

1.活动引入

在活动引入环节，教师首先展示《九章算术》“方田”章中的圭田面积问题，让学生利用所提供的三角形纸片，通过剪和拼来推导三角形面积公式。其中两组学生分别展示了平行四边形（如图12）和矩形（如图13）的拼法。第一组学生沿着三角形两边中点的连线剪开，将上方的小三角形倒置且与下方的梯形拼接在一起;第二组学生先沿着三角形底边上的高剪开，然后再沿着其余两边的中点剪开。两组学生在剪、拼的时候都用到了三角形两边的中点，由此顺利引出三角形中位线的概念。

2.定理探究

教师首先让学生猜想中位线的性质，然后引导学生将三角形转化为平行四边形、矩形和梯形进行证明。学生四人一组，展开了热烈的讨论，不仅再现了历史上的证明方法，还呈现了古人没有总结的证明方法。

第一组学生通过倍长中线构造三角形全等来证明（如图14）;第二组学生通过作高将三角形转化为矩形，与刘徽推导三角形面积公式的方法相同（如图15）;第三组学生取中位线DE的中点，构造两组全等三角形进行证明（如图16）。

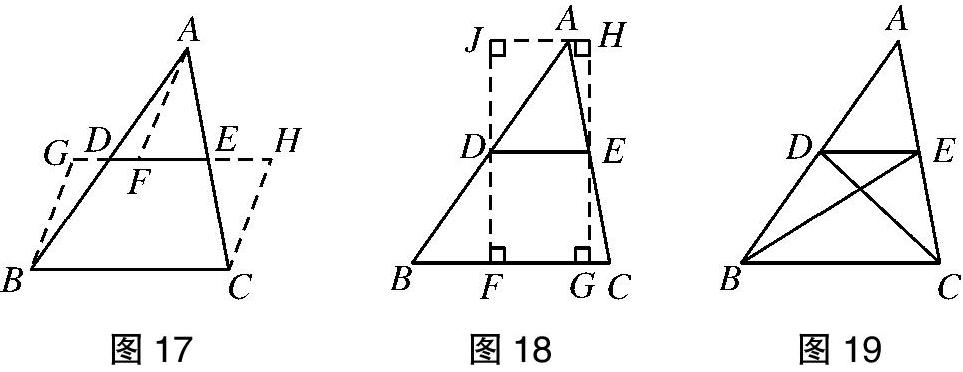
三组学生展示各自的方法之后，教师追问：“一定要在中位线上取特殊的点或者作高才可以证明吗？”一名学生提出，可以在中位线上取任意点构造两组全等三角形来证明（如图17）。接着，教师对上述的方法进行总结，并借助几何画板，拖动中位线DE上的点F，当点F移动到中位线端点处时对应的是第一组的证明;当点F分别移动到垂足和中点处时，所得图形分别对应于第二组和第三组的证明。还有一名学生过三角形两边中点分别作底边的垂线，从而将三角形转化为矩形，与刘徽推导三角形面积公式时所采用的另一种出入相补法一致（如图18）。有两名学生分别展示了将面积关系转化为边长关系来证明中位线与底边的位置关系和数量关系（如图19），这正是欧几里得在《几何原本》中采用的方法。

简短总结后，教师播放一段介绍三角形中位线历史的微视频，呈现三角形中位线的历史发展过程以及古人的不同证明方法。

3.新知应用

经历了前面的探究活动，学生的思维得到了拓展，因此新知应用环节进行得比较顺利;关于口答练习，学生构造出三角形，利用中位线定理来解答;例题讲解环节，在证明中点四边形与原四边形面积大小关系时，学生想到了利用三角形全等与面积等量代换两种方法，与前面证明定理时的转化方法相呼应。

4.课堂小结

学生的总结涉及内容、方法和思想，有的学生指出本节课学习了很多证明方法，而且方法之间有内在联系;有的学生提到作同一条辅助线可以有不同的解答;有的学生指出本节课的化归思想很多，有线面转化和图形之间的转化，通过割补法以及面积转化法来解决问题。最后，教师以“一个定理”（三角形中位线定理）、“两种思想”（化归思想与特殊到一般思想）、“三种方法”（平行四边形、矩形和梯形）、“四点启示”（古今联系、知识关联、数学文化、现实应用）对本节课进行总结（如图20）。

四、评价与启示

第四次教学后，高校研究者与HPM工作室教师从数学内容、认知需求、学习机会、学生表现度以及评价与运用5个维度[5]，从HPM视角对这节课作出评价。（1）在数学内容上，本节课选用的史料都是有文献依据的，体现了数学史料的科学性。引入的剪纸活动属于说理阶段，解决了为什么学习中位线、中位线概念的来源问题;定理探究环节，学生再现了历史上的证明方法，形成了古今对照;新知应用环节，引入瓦里尼翁四边形问题。这些都体现了数学史的有效性与可学性[6]。（2）在认知需求上，本节课对数学史的运用方式属于重构式，通过活动探究發现中位线概念并猜想中位线性质，再探究三角形中位线定理的证明方法，最后对定理加以应用。（3）在学习机会上，本节课的探究活动为所有学生创造了展示自我的机会。微视频建立了古今联系，提升了学生学习数学的自信心。（4）在学生表现上，探究成果丰硕，教学目标达成度高，学生总结比较到位。（5）在评价与运用上，同伴的掌声代替了执教者的反馈。

本节课也存在一些不足之处。一是教师提供的三角形彩纸太接近等腰三角形，对学生有误导;二是中点四边形面积问题占用了较多的课堂时间，淡化了本节课的主题;三是由于本节课的课堂容量较大，教师未能点明数学背后的理性精神与人文精神。从本次课例研究，我们得到以下启示。

其一，运用重构式时要充分把握史料之间的联系，将知识的历史序与学生的心理序相结合，帮助学生更好地理解和掌握知识，锻炼和提升能力。

其二，学生的能力不容低估，他们在探究活动中可能会有新的发现，因此，教师要给学生探究的机会。学生在课堂上的出色表现、课后作业的正确率以及访谈结果，都印证了这一点。

其三，古今联系是HPM视角下的命题教学的基本策略，而HPM微视频为古今联系提供了一条有效路径。古今联系缩短了学生与数学之间的心理距离，激发他们的学习兴趣，提升学习自信心。

其四，网络平台为课例研究提供了便利的条件。在未来，线上研讨必将成为HPM专业共同体开展课例研究的重要方式。

参考文献：

[1]张莉萍，栗小妮. HPM视角下的“三角形中位线定理”的教学[J].数学教学，2018（7）：11-15.

[2]欧几里得. 欧几里得几何原本[M].兰纪正，朱恩宽，译.西安：陕西科学技术出版社，2003.

[3]郭书春. 汇校九章算术[M].沈阳：辽宁教育出版社，2009.

[4]李霞，汪晓勤. 三角形中位线定理的历史[J].中学数学月刊，2016（9）：58-60.

[5]SCHOENFELD A H.What makes for powerful classrooms，and how can we support teachers in creating them？a story of research and practice，productively intertwined[J]. Educational Researcher，2014（8）：404-412.

[6]陈晏蓉，汪晓勤.数学史料的选取原则与案例分析[J].教育研究与评论（中学教育教学），2017（12）：37-43.

（责任编辑：陆顺演）