障碍物设置对人群荷载作用下连廊的减振控制

朱前坤 杨文斌 杜永峰

摘要： 研究了人群荷载作用下设置障碍物对连廊的减振控制。从考虑行人视线和障碍物作用区域两方面对传统社会力模型进行了改进，并对人群运动进行了仿真模拟。建立了人群荷载下连廊的振动控制方程，并进行动力响应求解。以某商贸城的钢结构连廊为算例，探讨了障碍物对人群速度等运动特性的改变，进一步对设置障碍物连廊的振动响应进行了分析，并从能量的角度阐述了减振机理。算例表明，布置障碍物后，行人平均步速最大下降率为9.1%;减振率随着障碍物数量的增加升高，多数工况减振率达到10%以上，最高减振率能达到30%;输入到结构上的能量明显降低，并且下降率与障碍物数量正相关。

关键词： 减振; 连廊; 社会力模型; 障碍物数量; 输入能

中图分类号： U448.11; TB535    文献标志码： A    文章编号： 1004-4523（2021）03-0507-08

DOI：10.16385/j.cnki.issn.1004-4523.2021.03.008

引 言

柔性结构具有低频率、低阻尼的特点，在人群荷载下易出现振动过量。而过量振动不仅易造成行人不适和心理恐慌，还可能诱发结构倒塌等严重的事故[1?2]。

目前对过量振动进行控制主要从改变振动系统的质量、阻尼、刚度三个方面进行。对振动系统的质量所产生的惯性力作出改变的方法以惯容器为主，该组件能够合成任意正实阻抗[3?5]。在结构上，惯容器能够以增加参振质量的方式改变振动系统的惯性力，减小振动系统的固有频率，使共振振幅降低[6?7]。通过调谐质量阻尼器（TMD）可增加结构阻尼，Zhu等[8]基于移动质量?弹簧?阻尼器的生物力学模型，采用不同优化参数的TMD对低频轻型人行桥进行了竖直振动舒适度研究，表明TMD能有效地降低人行天桥的共振。李晓玮等[9]以某人行桥实际工程为研究对象，通过设置TMD减振系统，验证了TMD减振系统在人行桥结构的减振上起到了良好效果，能满足行人对于振动舒适度的要求。而对结构刚度的改变可以利用半刚性连接装置来实现，如在装配式楼盖设计时采用半刚性连接装置的边界条件，通过调节刚度系数降低楼盖的加速度响应，使楼盖振动达到舒适度要求[10]。Zhu等[11]将人行天桥看作是一个两边具有半刚性约束的简支梁，研究表明：半刚性控制装置能够达到与调谐质量阻尼器同样良好的减振性能。以上方式都是通过增设改变振动系统参数的附加装置进行减振。由于人群的智能性，人群荷载与地震、风等荷载不同，其能够对周围环境灵活作出反应。连廊上的永久性（如长凳或灯杆）或临时性（护栏）设施除了发挥必要的功能性作用外，通过合理地布设，可以改变行人步行速度，打乱步进频率，使行走特性趋于不同，使施加到结构上的动荷载得到改变。由Helbing等[12]提出的社会力模型能够体现微观的个体行人间的相互作用和行走特性的差异性。基于社会力的微观模型已经用于模拟个人机动车辆（PMV）和行人混合交通[13]，對交叉路口的行人过街行为也能如实地体现[14]。Zhu等[15]基于社会力模型、减速机制和自停机制，对单向人流进行了模拟。从激励源，即人群运动控制的角度对结构进行减振，Venuti等[16]基于Mass Motion软件对人群运动进行了模拟，着重与TMD阻尼器减振进行了比较，研究了该措施的减振性能。在人致激励为主的结构中，通过合理设计，基于改变激励源的减振措施能够达到与传统减振方式相同的减振效果。

本文在前人基础上，以改变引发振动激励源的角度进行减振，采用能够体现行人拥挤和避让的传统社会力模型，并对其作出改进，对具体不同障碍物布设下人群运动进行仿真模拟。计算不同工况下的加速度时程响应，以峰值加速度作为评判结构振动的指标。以减振率定量化研究障碍物布置后产生的人群分布对结构振动的影响，并且从能量的角度对减振机理进行阐述。

1 行人遇障碍物绕行模型建立

1.1 社会力模型

社会力模型能够以各种作用力的形式体现行人之间及行人与障碍物之间相互作用，如自驱力、行人之间排斥力、行人受周围环境的排斥力等。

图1中表示行人的驱动力，为行人受到前方行人的心理排斥力，为当行人与行人之间接触时才会产生的物理排斥力，为行人与行人接触时产生的切向物理作用力;为行人受到上边界障碍物排斥作用而远离障碍物的心理排斥力，与分别为行人与上边界接触时产生的切向与法向的物理作用力;与分别为行人与通道中央障碍物接触时产生的切线和法向的物理作用力，为行人受到通道中央障碍物排斥作用的远离障碍物的心理排斥力。

以上各项社会力公式中各参数意义参考文献[17]。本文将通道内部行人受障碍物作用力分为沿通道和垂直通道两个方向，排斥力计算如下

式中 和为模型参数，分别代表行人与障碍物的作用力强度和作用范围。为行人半径与行人到障碍物的法向距离差;为由障碍物指向行人的单位法向量。

行人与障碍物之间物理作用力为

式中 为障碍物斜向挤压力;为与障碍物滑动摩擦力;为平行（垂直）于障碍物的单位切向力;为行人速度在障碍物方向上的投影;为人体正压力弹性系数（N/m）;为人体相对速度差摩擦系数（N·s/m2）;为通道方向，为垂直通道方向。

1.2 障碍物作用力模型改进

本文在引入减速避让机制[18]以及自停止机制[19]的基础上，考虑了行人视线及所处的不同障碍物作用区域，对社会力模型进行改进。障碍物出现在行人视觉范围内时，行人受障碍物排斥力开始减速，距障碍物超过安全距离后，开始避开障碍物进行绕行。行人受障碍物排斥力过大，速度小于0时，则令行人速度为0，行人停止运动后重新生成初始速度，而后继续行进或完成绕行。

行人与障碍物之间的作用力和行人之间作用力类似，有两侧边界对行人产生垂直边界的心理排斥力、减速避让力，沿边界方向的滑动摩擦力与垂直挤压力。通道内部设置的障碍物，与边界的不同之处在于行人在障碍物不同作用区域所受各项社会力不同。以矩形障碍物为例，如图2所示，在区域②④⑤，行人视线只能看到单侧障碍物边界，故只受一个方向的各项社会力;在区域①③，障碍物两侧边界都会出现在行人视线范围内，两侧障碍物边界均会使行人产生社会力，并且行人所受合力为两个方向社会力的矢量合;当行人绕过障碍物进入区域⑥，障碍物不在视线范围内，则行人只产生驱动力和行人之间作用力。

采用改进后障碍物作用力模型模拟人群运动，得到行人坐标、速度、质量等参数。通过行人步频与速度关系，及各阶动载因子计算竖向荷载Fp（t）[20]。

2 振动控制方程及能量转化

随机人群在连廊上的分布如图3所示。图中，M为单位长度质量，C为阻尼，I为惯性矩，ξ为阻尼比，E为弹性模量，L为连廊长度。

2.1 连廊的振动控制方程

在随机荷载作用下，连廊包含惯性力、阻尼力、弹性力、外荷载力的振动控制方程为

式中，等式右侧为人群荷载求和，表示第个行人;其中为Dirac函数，来表示移动人群荷载作用。具有如下三个性质：

2.2 振动控制方程的求解

采用振型叠加法，求解该振动控制方程。引入结构的位移变形函数

式中 为结构的几何位移坐标，为广义坐标，对应第阶振型的振型函数。

为了排除其他因素的干扰，使计算过程更便捷，连廊假定为简支梁，振动过程以一阶竖向振型为主，故其他阶的影响可忽略不计[21?24]，振型函数假定为正弦曲线。对式（9）两端沿全长积分，根据Dirac函数的性质，行人荷载力为

基于Matlab编程，利用Newmark?β法求解式（17），得到连廊的位移、速度、加速度。

2.3 人群-结构的能量转化

设置障碍物改变行人行走特性使施加到结构上荷载减小，从能量的角度体现为输入到连廊上的能量减少。行人荷载在行走过程中产生的位移、速度，因质量、阻尼、刚度的存在而做功。人群荷载产生的输入能施加在连廊后，进一步转化为连廊的质量动能、黏滞阻尼能、弹性应变能，引起结构振动响应。因此可以引入一种能量计算公式[16，25?26]，并将其应用于动态响应分析中。利用上述Newmark?β方法计算所得速度、位移、人群荷载，通过功能关系对能量进行计算。

结构响应计算流程图如图4所示。

3 算例分析

某商贸城的钢结构连廊跨度L=21.8 m，宽度为W=3 m，结构的阻尼比ξ = 0.01。该钢结构连廊边界条件为梁端铰接，并且满足条件的构造措施，不会造成落梁。截面竖向等效抗弯刚度为EI = 3.268×109  N·m2，单位长度质量M = 1063.5 kg/m，阻尼系数C=950.8 N/（m·s-1），结构的一阶频率为5.79 Hz。

3.1 连廊上障碍物布置规则

在该连廊上布置障碍物，参考连廊中通常可见的永久性长凳、灯杆和临时性的护栏等障碍物[27?28]。本文采用如图5所示的两种障碍物布置方式，障碍物面积统一为0.3×0.3 m?。障碍物布设应当沿直线排列，并且遵循均匀、等间距的原则，此外还应当给行人预留足够的行走空间。图5所示为两种布置方式最密集障碍物布置状态，障碍物数量分别为11和22，障碍物面积占整个人行通道面积比例为1.51%和3.03%。除此之外的其他不同障碍物数量布设参数如表1所示。

3.2 人群运动的仿真实现

利用Matlab平台对人群及障碍物进行仿真模拟，通道参数同上述连廊。行人质量、期望速度、行人半径等参数参考文献[17]。普通成年人的步长一般在45?65 cm之间，考虑到小孩的步长偏小（在30?40 cm之间）及行人遇到障碍物减速后步长趋于减小，使步长在30?65 cm之间随机生成。行人进入障碍物作用区域（0.65×0.65 m2）后，开始受障碍物所产生的社会力而减速，距障碍物距离超过安全距离（0.3 m）后开始绕行。以障碍物中线为界，行人在障碍物上侧向上绕行，下侧向下绕行。绕行表现为坐标增减，由于行人前进方向（方向）受障碍物阻挡，故该方向步长增减较小，主要通过对连廊宽度方向（方向）的坐标增减步长来实现。

当障碍物数量为14，行人密度为0.76人/m?，t=24 s时刻的仿真模拟如图6所示。结果表明Matlab平台模拟下行人能够对障碍物进行有效避让和绕行，行人趋于沿两侧边界和通道中线附近空间运动，与实际行人运动相吻合。

3.3 人群速度-密度关系

选取2?100人范围内的10种不同行人密度工况，对人群和障碍物进行仿真。设置障碍物后，进入仿真通道的人群在障碍物作用范围会出现新的分布，障碍物排斥力等社会力作用下行人速度会减小，行人平均速度受障碍物的影响。取4组计算平均步速的均值，得图7中人群速度?密度关系曲线。

与无障碍作用下拟合的平均速度?密度曲线[17]比较，可得设置障碍物后行人平均速度明显降低，并且其值随着障碍物数量的增加而减小，减小率最大值为9.1%。图7中，低密度行人状态下，增加障碍物数量对行人平均速度减小较为明显，当行人密度超过0.8?1.0人/m?时，障碍物增加对平均速度影响较小。这是由于人群密度过高时，过于拥挤，行人步速普遍趋于较小值，障碍物影响减弱。仿真结果与实际行人运动特性相符，说明了社会力模型模拟障碍物、行人的合理性。

3.4 设置障碍物连廊振动响应分析

《建筑楼盖结构振动舒适度技术标准》[29]中指出，连廊的一阶竖向自振频率不宜小于3 Hz，不封闭连廊竖向峰值加速度限值为0.5 m/s2，超过这一限值，行人会产生不舒适。

以连廊上设置6个障碍物，通过40人为例计算结构响应，计算原理和方法见2.2节。加速度时程与加速度1 s?均方根如图8所示。图中细线为加速度时程曲线，粗线代表加速度1 s?均方根曲线。可以看出，设置障碍物后结构加速度峰值从无障碍物时的0.472 m/s?减小为0.403 m/s?，加速度1s?均方根峰值从0.243 m/s?减小为0.159 m/s?。为了定量化研究障碍物数量增加对结构响应的影响，定义设置障碍物后加速度峰值下降量与无障碍时加速度峰值的比值为减振率。经计算，减振率为14.6%，由此可知设置障碍物后结构振动响应有效降低。结构峰值加速度降低，满足舒适度要求，从而不会使行人产生不适。

利用傅里叶变换将结构响应从时域变为频域，得到如图9所示的傅里叶谱。峰值傅里叶谱从0.0309 m/s?下降为0.0190 m/s?，进一步说明通过设置障碍物控制人群荷载对结构进行减振的有效性。

3.5 障碍物布置对结构减振率影响

由于行人坐标位置、期望速度、初始速度、距障碍物距离等因素的随机性及模拟试验的非稳定性，同一工况下产生的人群分布引起的结构响应可能不同，故选取0.15?1.53人/m?的10种不同行人密度工况各计算4组数据的平均加速度峰值及平均减振率，结果如表2所示。

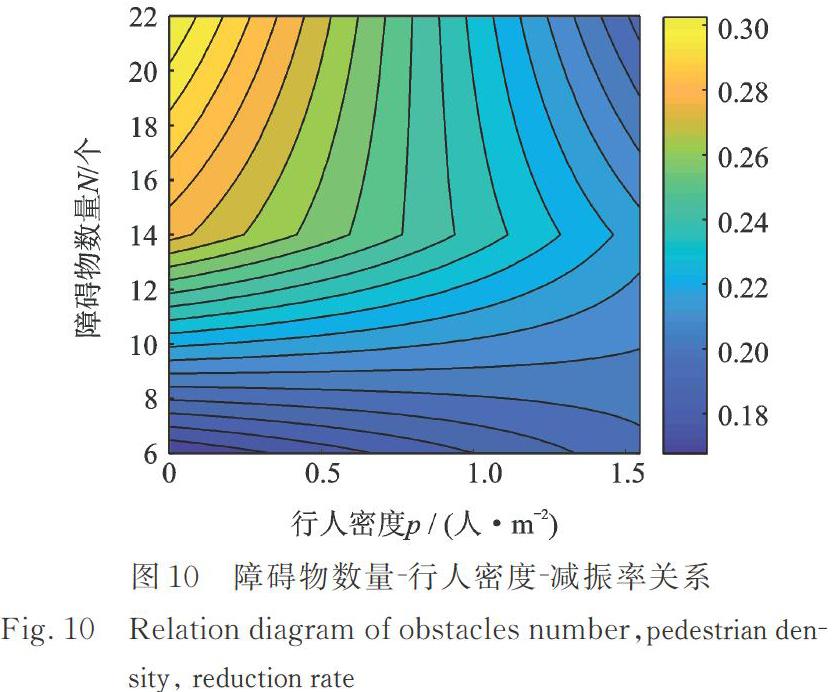
为了更加直观地分析减振率与障碍物数量、行人密度之间的关系，以该三个参数绘制填充等高线图，如图10所示。图中颜色越浅表明减振率越大，减振性能越好。减振率随着障碍物数量的增加而增大。行人密度较低时，障碍物增加对减振率影响较大，减振效果显著，但当连廊上行人密度超过1人/m2后，障碍物增加对结构减振率的影响趋于不明显。这主要是由于当行人密度过大时，连廊上行人之间过于拥挤，行人行进不通畅，速度普遍较低并且趋于一致，增加障碍物对人群运动影响不明显。

3.6 结构减振机理分析

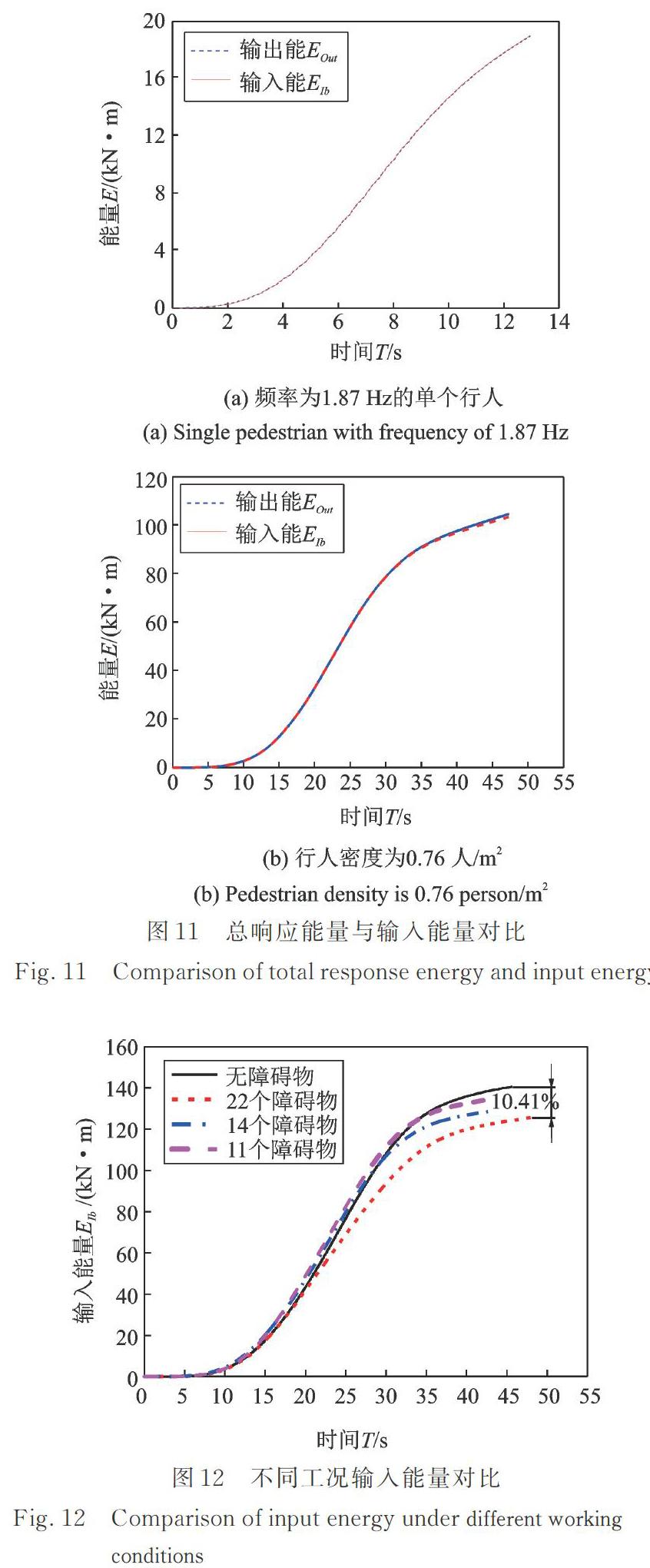
从输入能累积量的角度分析设置障碍物连廊的减振机理。根据2.3节的能量转化机理，由能量平衡方程（19），可知输入到结构上的输入能应该与转化后的质量动能、黏滞阻尼能、弹性应变能三项之和相等。行人步频一般在1.65?2.10 Hz之间，故取平均值1.87 Hz。单个行人以该频率通过连廊，输入能与结构总能量如图11（a）所示。图11（b）为障碍物数量为11、行人密度为0.76人/m2工况下两能量的对比图，此工况行人和障碍物较均匀。由图11（a）?（b）可知，此两种工况下，两能量之间的最大误差分别为0.2%， 1.1%。因此，行人荷载产生的输入能与转化后结构上其他三项能量之和在误差允许范围内守恒。

图12给出了障碍物数量为11，14，22三种情况与无障碍物时输入能对比图。图12中在整个响应期间，设置障碍物控制进入连廊的人群，输入能明显降低。三种工况下输入能最大减小率分别为4.06%，8.21%，10.41%。14个障碍物工况下，能量累积曲线包络在10和22个障碍物之间。这是由于响应初期进入结构行人数量有限，障碍物数量对结构响应不明显;响应后期行人全部进入，障碍物阻挡效果显著。计算其他工况下连廊上的输入能平均值，如表3所示，可以看出，输入能减小率与障碍物数量有正相关性。

4 结 论

1）考虑行人视线和障碍物作用区域，对社会力模型进行了改进。算例表明设置障碍物后行人平均步速减小率在4%?5%之间，最大达到9%，与实际人群运动相符，说明了改进的社会力模型模拟障碍物、行人的合理性。

2）为人致激励下柔性结构减振提供了一种可行方案。算例中随着障碍物数量的增加，结构减振率越高，障碍物数量大于6后，减振率都能达到10%以上，最高减振率可达30%;人群密度较低时，障碍物增加对减振率影响较大，人群密度大于1人/m2后，障碍物增加对结构减振率的影响不明显。

3）从能量的角度对结构减振机理进行了解释。算例中设置障碍使连廊上的输入能有效降低，减小率在2.33%?10.41%之间，并且能量减小率和障碍物数量有正相关性。

参考文献：

[1] 法永生， 李  东， 孙翠华，等. 人行桥随机人行荷载下的振动分析及其舒适度评价的新方法[J]. 振动与冲击， 2008， 27（1）：119-123.

Fa Yongsheng， Li Dong， Sun Cuihua，et al. Vibration analysis for a footbridge under stochastic pedestrian load and a new method for comfort evaluation[J]. Journal of Vibration and Shock， 2008， 27（1）：119-123.

[2] 彭建蕤， 羅晓群， 张其林. 某拱索支撑人行桥人致振动响应分析及控制[J]. 建筑结构， 2017， 47（S1）：569-573.

Peng Jianrui， Luo Xiaoqun， Zhang Qilin. Response analysis and vibration control for arch and cable supported pedestrian bridge under human walking excitation[J]. Building Structure， 2017， 47（S1）：569-573.

[3] Smith M C. Synthesis of mechanical networks：The Inerter[J]. IEEE Transactions on Automatic Control，2002， 47（10）：1648-1662.

[4] Papageorgiou C， Smith M C. Laboratory experimental testing of inerters[C]. Proceedings of the 44th IEEE Conference on Decision and Control， Seville， Spain， 2005：3351-3356.

[5] Chen M Z Q， Papageorgiou C， Scheibe F， et al. The missing mechanical circuit element[J].IEEE Circuits and Systems Magazine， 2009， 9（1）：10-20.

[6] 溫华兵， 昝  浩， 陈  宁，等. 惯容器对隔振系统动态性能影响研究[J]. 实验力学， 2015， 30（4）：483-490.

Wen Huabing， Zan Hao， Chen Ning， et al. Study of the impact of inertia container on the dynamic properties of vibration isolation system[J]. Journal of Experimental Mechanics， 2015， 30（4）：483-490.

[7] 孙晓强， 陈  龙， 汪少华，等. 非线性惯容器-弹簧-阻尼悬架系统隔振性能分析[J].农业工程学报， 2013， 29（23）：38-45.

Sun Xiaoqiang， Chen Long， Wang Shaohua， et al. Analysis of vibration isolation performance for nonlinear inerter-spring-damper suspension[J]. Transactions of the Chinese Society of Agricultural Engineering， 2013， 29（23）：38-45.

[8] Zhu Qiankun， Li Hongnan，Nan Nana， et al. Vibration control of pedestrian-bridge vertically dynamic coupling system based on biodynamic mode[J]. Journal of Southeast University， 2017，32（2）：209-215.

[9] 李晓玮， 何  斌， 施卫星. TMD减振系统在人行桥结构中的应用[J]. 土木工程学报， 2013， 46（1）：245-250.

Li Xiaowei， He Bin， Shi Weixing. Application of TMD seismic vibration control system in the bridge structures[J]. China Civil Engineering Journal， 2013， 46 （1）：245-250.

[10] 朱前坤， 蒲兴龙， 惠晓丽，等. 考虑人-结构相互作用装配式轻质楼盖振动舒适度评估[J]. 建筑结构学报， 2019， 40（11）：220-229.

Zhu Qiankun， Pu Xinglong， Hui Xiaoli， et al. Assessment of vibration serviceability of precast lightweight floor considering human-structure interaction[J]. Journal of Building Structures， 2019， 40 （11）：220-229.

[11] Zhu Q， Hui X， Du Y， et al. A full path assessment approach for vibration serviceability and vibration control of footbridges[J]. Structural Engineering and Mechanics， 2019， 70（6）：765-779.

[12] Helbing D， Molnar P. Social force model for pedestrian dynamics[J]. Physical Review E，1995， 51（5）： 4282.

[13] Charitha D， Miho I A， Hiroaki N， et al. Calibrating a social force based model for simulating personal mobility vehicles and pedestrian mixed traffic[J]. Simulation Modelling Practice and Theory， 2018， 87：395-411.

[14] Zeng W， Chen P， Nakamura H， et al. Application of social force model to pedestrian behavior analysis at signalized crosswalk[J]. Transportation Research Part C：Emerging Technologies， 2014， 40：143-159.

[15] Zhu Q， Hui X， Du Y， et al. Study on the vertical dynamic coupled effects of the crowd structure system based on the social force model[J].KSCE Journal of Civil Engineering， 2019，23（5）：2243-2253.

[16] Venuti F， Reggio A. Mitigation of human-induced vertical vibrations of footbridges through crowd flow control[J]. Structural Control and Monitoring Health， 2018，25（12）： e2266.

[17] 张  琼， 南娜娜， 朱前坤，等. 随机人群运动荷载作用下大跨度连廊的振动响应[J]. 土木与环境工程学报， 2019， 41（2）：99-105.

Zhang Qiong，Nan Nana， Zhu Qiankun， et al. Vibration response of long-span corridor under stochastic crowd load[J]. Journal of Civil and Environmental Engineering， 2019， 41（2）：99-105.

[18] 李珊珊， 钱大琳， 王九州. 考虑行人减速避让的改进社会力模型[J]. 吉林大学学报（工学版）， 2012， 42（3）：623-628.

Li Shanshan， Qian Dalin， Wang Jiuzhou. Improved social force model considering pedestrian deceleration to avoid collision[J]. Journal of Jilin University （Engineering and Technology Edition）， 2012， 42（3）：623-628.

[19] Parisi D R， Gilman M， Moldovan H. A modification of the social force model can reproduce experimental data of pedestrian flows in normal conditions[J]. Physica A， 2009， 388（20）：3600-3608.

[21] 张  琼， 南娜娜， 朱前坤， 等. 基于行人动力学模型的人-桥竖向动力相互作用[J]. 重庆大学学报（自然科学版）， 2017， 40（4）： 93-100.

Zhang Qiong，Nan Nana， Zhu Qiankun， et al. Pedestrian bridge dynamic interaction in the vertical based on biodynamic model[J]. Journal of Chongqing University （Natural Science Edition）， 2017， 40 （4）： 93-100.

[22] ?ivanovi? S. Benchmark footbridge for vibration serviceability assessment under the vertical component of pedestrian load[J]. Journal of Structural Engineering， 2012， 138（10）： 1193-1202.

[23] 朱前坤， 李宏男， 杜永峰，等. 不同行走步速下人行桥振动舒适度定量化评估[J]. 工程力学， 2016， 33（10）：97-104.

Zhu Qiankun， Li Hongnan， Du Yongfeng， et al. Quantitative evaluation of vibration serviceability of pedestrian bridge under different walking speed[J]. Engineering Mechanics， 2016， 33（10）：97-104.

[24] Van Nimmen K， Lombaert G， De Roeck G， et al. The impact of vertical human-structure interaction on the response of footbridges to pedestrian excitation[J]. Journal of Sound and Vibration， 2017， 402：104-121.

[25] Ahmadi E， Caprani C， ?ivanovi? S， et al. Vertical ground reaction forces on rigid and vibrating surfaces for vibration serviceability assessment of structures[J]. Engineering Structures， 2018， 172：723-738.

[26] 李祥秀， 譚  平， 刘良坤，等. 基于功率法的TMD系统参数优化与减振性能分析[J]. 振动与冲击， 2014， 33（17）：6-11.

Li Xiangxiu， Tan Ping， Liu Liangkun， et al. Parametric optimization and aseismic performance of a TMD system based on power method[J]. Journal of Vibration and Shock， 2014， 33（17）：6-11.

[27] Brownjohn J M W. Energy dissipation from vibrating floor slabs due to human-structure interaction[J]. Shock and Vibration， 2001， 8（6）：315-323.

[28] Helbing D， Buzna L， Werner J T. Self-organized pedestrian crowd dynamics： Experiments， simulations， and design solutions[J]. Transportation Science， 2005， 39（1）：1-24.

[29] 娄 宇， 吕佐超， 黄 健， 等. JGJ/T 441-2019， 建筑楼盖结构振动舒适度技术标准[S]. 北京： 中国建筑工业出版社， 2019.

作者简介： 朱前坤（1981?），男，教授。电话：13679488676;E-mail：zhuqk@lut.cn

通讯作者： 杨文斌（1996?），男，硕士研究生。电话：18809424681;E-mail：1638433610@qq.com