怎么做能让长方体表面积的练习更有效
黄建


长方体表面积的计算过程相对比较烦琐,相关的练习常常让学生感到厌烦。为了让长方体表面积的计算练习更有效,教师可设计“以画为主,以算为辅”的教学活动。
一、画差异
(一)呈现问题
学习了长方体的体积和表面积后,两位同学有了这样的讨论。
他们用的算式都是6×6×6,表示的意思一样吗?如果不同,请画一画,让其他人能看懂你的想法。
(二)展示交流
学生画出了如下示意图(如图1)。
在交流中教师引导学生体会:
虽然算式都是6×6×6,但两个算式表示的意义不同:表面积是面的大小,体积是所占空间的大小。求表面积时,先算的“6×6”求的是一个面的大小,再乘6求的是6个面的大小。而计算体积时,6×6×6表示摆1×1×1的小立方体,一行可以摆6个,一层摆6行,可摆6层。计算结果的单位也不相同:求表面积大小时结果用面积单位表示,求体积大小时结果用体积单位表示。
二、画联系
(一)呈现问题
(二)展示交流
1.得出结论:你认为哪个算式是正确的?
预设:为什么不选择D?它不是在算表面积,那它在算什么?B错在哪里?从哪里看出来这是在求5个面的面积?怎么修改能求出它的表面积?
2.沟通联系:前三种方法有什么联系和区别?
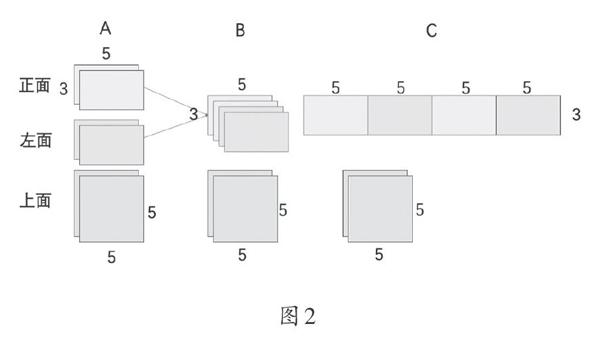
教师借助图形表征(如图2),引导学生明确这三种方法分别求了几个面的面积。
三、画思路
(一)呈現问题
下面两个立方体木块,按照哪一种方法切割,表面积增加得更多?说明理由。
(二)展示交流
1.相互交流:你们的结论是什么?你是怎么想的?
2.引导思考:①同样是方案一,还有不同的方法来计算增加的表面积吗?②方案二中,有同学写了这样一个算式:8×8×6,你能看懂吗?还可以用不同的方法来比较吗?
3.画图表征:能否不计算,就能比较出大小?想一想,尝试画图说明。
4.进阶提升:同样是切三刀,切割后的图形表面积增加384cm2,还可以怎么切?请画一画。
这样设计长方体表面积的练习,可以让学生在画差异中,多维辨析,理解公式;在画联系中,多元对比,巩固方法;在画思路中,多向应用,内化意义。

