凸显数学本质:构建具有深度学习特质的数学课堂
黄丽冷

【摘要】找准认知起点,激活已有经验,是深度学习的关键;直逼数学本质,亲历知识的形成过程,是深度学习的核心;注重数学思考,触动思维内核,是深度学习的归宿。教学中,教师要基于学生原有的认知起点,紧扣知识本质,激活数学思维,发展核心素养,使学习向深处漫溯,构建具有深度学习特质的数学课堂。
【关键词】认知起点;数学本质;数学思考;深度学习;数学课堂
小学数学深度学习是以数学学科的核心内容为载体,以提升学生的学科素养为目的,把握数学本质,通过精心设计问题情境,引发学生认知冲突,组织学生全身心参与学习活动,围绕具有挑战性的学习主题进行深度探究,从而使学生获得成功体验和发展的有意义的学习过程。因此,在教学中,教师要坚持以“学为中心”的理念,尊重学生已有的认知经验,凸显数学本质,挖掘、拓宽学生思维的深度与广度,培育数学核心素养,才能构建具有深度学习特质的数学课堂。
一、探寻认知起点,触摸数学本质
奥苏伯尔认为:“影响学习最重要的因素是已知的内容和已有的认知结构。”教学中,教师要立足学情,探寻学生的认知起点,使学生的学习落在支撑点上,让深度学习有着力点,基于原有的认知起点,以其所知,喻其不知,愤悱求知,新知自然生成。
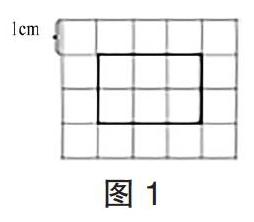
师:这个长方形的面积是多少?(如图1)你是怎么想的?
生1:这个长方形的面积是6cm2。我是这样想的,这个长方形的长是3cm,宽是2cm,长方形的面积等于长乘宽,所以面积是3×2=6cm2。
师:为什么长方形的面积等于长乘宽?谁会讲道理?
生2:这个长方形有2行,每行有3个方格。3×2=6,面积就是6cm2。
师:每个方格就是一个单位面积。计算长方形的面积就是算一算它一共有多少个单位面积。长看的是什么?宽看的又是什么?
生2:长看的是每行有几个单位面积,宽看的是有几行。每行个数乘以行数,一共有几个单位面积,面积就是多少。
长方形面积知识是平行四边形面积知识的生长点。通过对长方形面積推导过程的回顾,调动学生原有认知,唤起学生对面积本质的回忆,理解面积是通过计数单位面积数来刻画的。长方形的面积就是用每行单位面积数乘行数来计算的,对应的就是长和宽这两个维度的量,聚焦度量本质,唤醒学生对“长”和“宽”的深度理解,触摸数学本质。
二、亲历整体架构,直击数学本质
新课标指出:“学生学习应当是一个生动活泼的、主动的和富有个性的过程。”积极思考、动手实践、自主探索、合作交流等,都是学习数学的重要方式。教师在课堂教学实践中应创设开放式的探究空间,引领学生深度探究学习,深入思辨,通过辨析、沟通、建立联系,直击数学本质,摒弃非本质的干扰,亲历知识的整体建构与形成过程。
探究活动一:这个平行四边形的面积是多少?(如图2)在方格图中数一数,并把数的过程在图上表示出来,让大家能看明白你是怎么数的。
生1:我是先数中间整格的,有4格,再把不是整格的移过来数一数(上下移),有2个。合起来一共有6格,就是6cm2。
生2:我把不满一格的移成整格后,有2行,每行有3个方格,面积是3×2=6cm2。
生3:每行有3格,也就是每行有3个单位面积,有2行,用每行的个数乘行数,一共有6个单位面积,平行四边形的面积就有6cm2。
生4:我有疑问。这样一移,形状变了,数出来的面积和原来的平行四边形的面积一样吗?
生3:虽然移动了,但是所占的格子的总数是不变的,所以数出来的面积和原来平行四边形的面积是一样的。
生4:我明白了,用凑整的方法,把不满整格的部分平移凑成整格来数,一共有几个单位面积,面积就有多少。
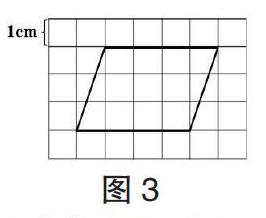
探究活动二:这个平行四边形的面积是多少?(如图3)在方格图上数一数,并把数的过程在图上表示出来,让大家能看明白你是怎么数的。
生1:我先把不满整格的部分,平移凑成整格(左右移)。移动3次后,每行有4个方格,有3行。面积是就是4×3=12cm2。
生2:我有补充,我直接从左边分出一个三角形,然后整个三角形平移,拼在图形右边,变成一个长方形,每行有4个方格,有3行,面积是4×3=12cm2。
生3:第一种方法得移动3次,第二种方法直接把左边多出来的这个三角形,平移补到图形右边,只要移动一次,更简洁。
生4:第二种方法把左边的三角形移动到右边后,变成了长方形。每行有4个方格,有3行,面积是4×3=12cm2。可以直接根据长方形的面积公式来计算。
探究活动三:这个平行四边形的面积是多少?(如图4)
师:现在不动手移了,能不能告诉大家,这个平行四边形有几个单位面积?小组同学说说自己的想法。
生1:这个平行四边形有20个单位面积,面积是20cm2。
生2:这个平行四边形一行有5个单位面积,有4行。5×4=20cm2。
生3:我发现平行四边形的面积和长方形的面积一样,也是用每行单位面积的个数乘行数来计算的。
师:一行有几个看哪里?有几行又是看哪里?
生2:一行有几个看的是底,有几行看的是高。
生3:每行单位面积的个数看的就是平行四边形的底,行数看的就是平行四边形的高,平行四边形的面积等于底乘高。
生4:为什么几行看的是这条(高),而不看这条(邻边)?
生2:这条(指着邻边)移过去了,看不到了。
生3:邻边移过去后,邻边藏起来了,而高露出来了。
师:同学们眼睛里看到的是平行四边形,脑子里想的却是长方形。这样的方法在数学上称为“转化法”。
“数方格”是测量本质的直观体现。活动一,从“数方格”切入,紧扣面积本质。学生在数方格的过程中,本能地把不是整格的部分移补成整格来计数,在移补和计数方格的过程中渗透转化法,深刻体会了“等积变形”。活动二,关注知识本质,优化解决方法。在不同方法的对比中,体会移补、转化成长方形的优势,沟通两种图形面积之间的本质联系,继续渗透测量本质和转化法,为平行四边形面积公式的推导埋下伏笔。活动三,脱离实物操作,发展空间想象。“眼睛里看到的是平行四边形,脑子里想的却是长方形”“邻边移过去后,邻边藏起来了,而高露出来了”“平行四边形面积等于底乘高”的道理也就跃然纸上了。
“水尝无华,相荡乃成涟漪;石本无火,相击而发灵光。”基于“数方格”与“转化法”之间的联系,学生由“动手移”到“动脑移”,由“数方格”到“看长度”直接计算,由具体操作到抽象感知,既积累了数学活动经验,又发展了数学思维能力和空间想象能力,亲身经历了知识的整体架构,知识的本质深深烙进心里。
三、基于深度学习,内化数学本质
深度学习是一种基于理解的学习,是一种进行深入思考和深入探究的学习,它不仅关注学生学习的结果,而且重视学生的学习状态和学习过程。围绕具有挑战性的、触及数学本质的学习主题,能够有效快速地激活学生的数学思考,触动学生思维内核,真正实现认知上的超越,深化学生对数学本质的理解,使学习向深处漫溯。
(一)紧扣本质,突破盲点
师:这个平行四边形停车位的面积是多少?
生1:5×2.4=12(平方米)。
生2:3×2.4=7.2(平方米)。
生1:3×2.4是错误的,因为3米和2.4米不对应。
生1:(上台边画图边解释)把左边的三角形平移到右邊后,得到的长方形长5米,宽2.4米,所以停车位的面积应该是5×2.4=12(平方米)。
生2:如果要用3米的底来计算,怎么办?
生1:如果要用3米的底来计算,那得测量出3米这条底边上的高。(课件顺势出示另一组对边上的高4米。)
生1:现在计算平行四边形的面积也可以用3×4=12(平方米),两种计算方法结果相同。
师:关于平行四边形面积的计算,你要提醒大家注意什么?
生1:计算平行四边形的面积,必须用对应的底乘高。
心理学家赫茨伯格认为:“有挑战性的素材能更好地激励学生学习,能给学生带来乐趣。”教师以停车位为载体,给出多余条件,选择合适数据,强化对应关系,有效突破“对应的底和高相乘”这个认知难点和易错点,同时创设了静下心来反思的时间和空间,深化了学生对知识本质的理解。
(二)深入本质,走出误区
师:(几何画板演示将长方形框架拉动成平行四边形的过程)你有什么发现?
生1:拉动长方形框架后变成了平行四边形,越往下拉,这个平行四边形越扁。
生2:平行四边形变扁了,面积变小了。
生3:平行四边形变扁了,也就是高变矮了。
生4:拉动过程中,底都不变,也就是每行的单位面积的个数不变,但高变矮了,也就是行数变少了,所以面积变小了。
生5:拉动长方形框架后,面积变小的原因在于高变矮了。
生6:拉动框架后,底边和邻边不变,面积却变小了,这也说明了平行四边形的面积不能用底边乘邻边。
弗赖登塔尔认为:“反思是数学思维活动的核心和动力。”教师借助长方形框架,引导学生深度思考辨析,深入说理表达,进一步理解平行四边形的面积不能用邻边相乘的道理,内化知识本质,实现知识的深度建构。
凸显数学本质是在新知生成和数学学习的基础上进行数学思想方法的渗透,并在教学实践中通过找准学生的认知起点,打破原有的认知结构,沟通知识的内在联系的策略,深化学生对数学本质意义的理解,掌握重要的思想方法,提升数学的核心素养,使学生数学学习走向深度,向更深处、更远处漫溯,从而构建起具有深度学习特质的数学课堂。
【参考文献】
俞正强.种子课[M].北京:教育科学出版社,2013.

