台阶地形对爆破振动速度影响研究
邹南荣,孙明武
(1.紫金矿业集团股份有限公司 紫金山金铜矿,福建 上杭县 364200;2.福州大学 紫金矿业学院,福建 福州 350116;3.福州大学 爆炸技术研究所,福建 福州 350116)
0 引言
分析露天矿山爆破开挖工程中爆破振动速度的传播规律具有重要意义。目前,在对台阶地形对爆破振动的影响研究中,大多数采用现场试验、理论分析及数值模拟等手段进行相应的研究[1−7]。罗周全等[8]基于爆破等效动力荷载理论及有限元分析模型,将现场实测与数值分析相结合,研究了采场爆破开挖对边坡动力稳定性的影响。周俊汝等[1]引入介质阻尼项建立的黏性岩体爆破振动频谱表达式,数值模拟分析了爆破地震波传播过程中的振动频率及衰减规律。孙志超等[4]基于连续损伤本构模型,数值模拟岩土台阶爆破过程,研究了台阶爆破振动传播规律。武旭等[7]利用ANSYS/ LS-DYNA有限软件进行数值模拟,并结合现场振动监测试验数据,研究了台阶地形对爆破振动速度的影响。
本文通过数值模拟软件对露天台阶爆破进行相应的研究,并结合现场爆破振动试验数据分析结果,分析台阶高度对爆破振动传播规律的影响,为露天矿山爆破振动的传播规律研究提供一定的依据。
1 爆破模型及参数设置
1.1 参数的选取
基于有限元软件ANSYS/LS-DYNA 模拟炸药的动力冲击作用,模拟台阶爆破,并根据其本身性质的不同选取不同的状态方程[9]。
(1)炸药的状态方程及参数。此次模拟采用公认度较高的炸药爆炸JWL状态方程来描述[9]:
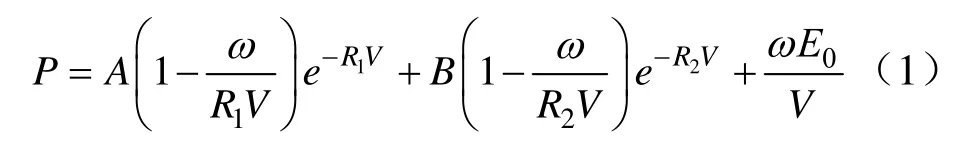
式中,ω、A、B、R1、R2为炸药特性参数,A=214.4 GPa,B=0.182 GPa,R1=4.2,R2=0.9,ω=0.15;P为JWL状态方程的爆轰压力;V为爆轰产物的相对体积;E0为初始化内能,E0=4.192 GPa。其岩石物理力学参数[10]见表1。

表1 矿岩物理力学参数
(2)空气介质的状态方程及参数。空气采用材料来实现,同时用线性多项式状态方程描述空气的作用[6−7,9]:
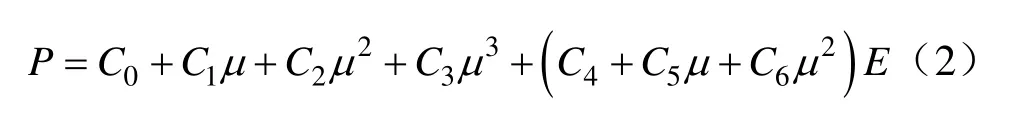
式中,C0~C6为方程参数,C4=C5=0.4,其余均为0;E0表示空气初始比内能;μ为体积比。
1.2 模型建立
利用有限元软件ANSYS/LS-DYNA 创建相应的爆破模型,则边坡爆破各模型尺寸为:台阶高度H分别为7 m、8 m、9 m、10 m、12 m、14 m;坡面角为70°。如图1 所示,创建合理的计算模型,为了缩短计算时间,对网格进行合理的划分。

图1 计算模型
2 数值模拟结果与分析
当坡面角一定,创建台阶高度分别为7 m、8 m、9 m、10 m、12 m、14 m 的数值模型,模型计算时间0.05 s。利用LS-PrePost 后处理程序对其建立的模型进行分析,提取监测点(见图2)的临界振动速度,其不同时刻的振动速度云图如图4 所示。

图2 数值模拟时程记录点编号
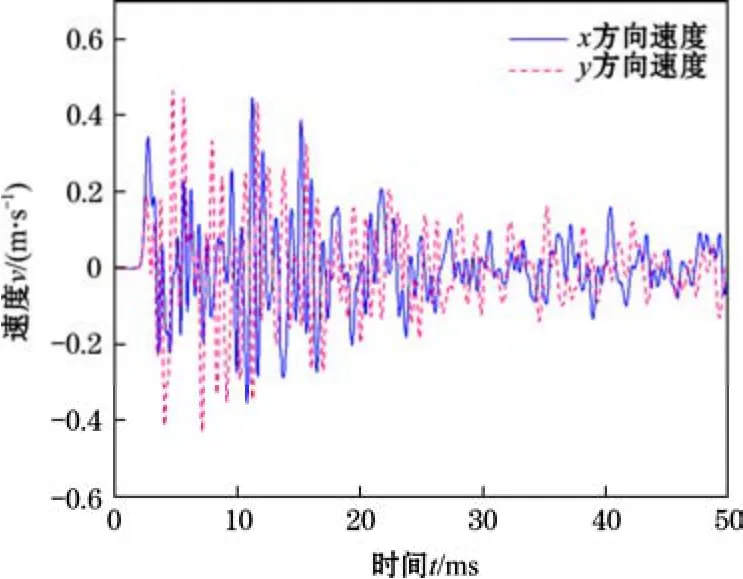
图3 监测点1 表面速度时程曲线
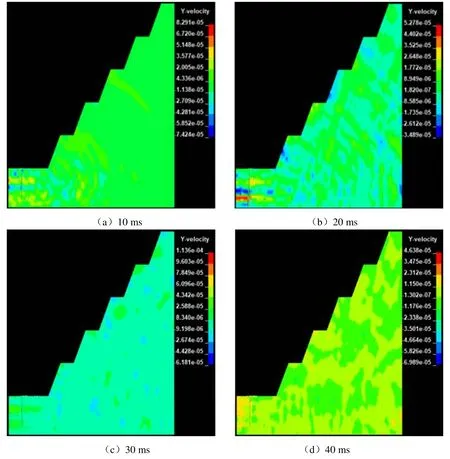
图4 不同时刻振动速度云图
图5 同一坡底1,3,5,7,9 号测点的包络线表明:台阶地形对于表面振动影响随着距离的传播整体上呈指数衰减;从质点峰值可以看出,就单个台阶而言,上部台阶坡顶处出现异常峰值,这是由于台阶高差的存在导致产生放大效应,同时也是由于自由面数量对应力波的叠加所造成的。从图5 还可以看出,当爆心距和高差在一定值时,质点振速产生高程放大效应。以竖直方向峰值振速为例,当台阶高度为12 m 时,其振速的放大效应出现在第3级台阶处,其放大倍数大约为1.01 倍。

图5 质点峰值振动速度随高程变化曲线
图6 表明:根据H=7 m、8 m、9 m、10 m、12 m 和14 m 之间放大效应的比值可以发现,速度放大倍数不会随着台阶高度的增加呈正相关,而是呈先增大而减小的趋势。这一现象正好证明高程对振动波既放大又衰减。

图6 放大倍数随着高程变化曲线
3 反映高程的数学模型分析
根据上述数值模拟分析结果以及相关研究可知[2−7]:高陡边坡爆破振动速度在一定高差内存在放大效应,而传统的萨道夫斯基公式不能体现其特性,故对其进行改进[7],从而有效地提高边坡爆破振动速度预测的精确性。
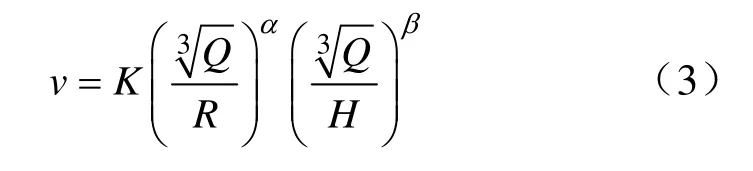
式中,R为测点到爆破中心的水平距离;α、β为与地质条件有关的系数;H为测点到爆源的垂直距离。由于岩体的物理力学参数一定,则有[2]:
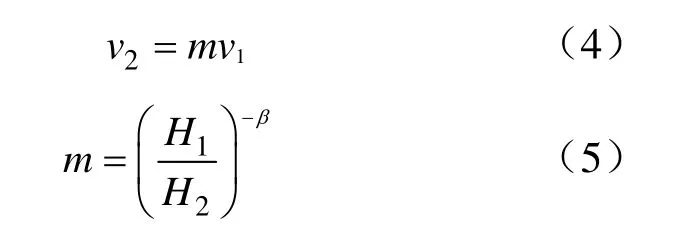
式中,v1和v2分别为高程低和高处的质点振动速度;m为放大系数;H1和H2为计算点高程。
4 工程应用实例
某矿山现开采标高在1835~1925 m 之间,炮孔直径为165 mm,孔深为10~12 m,超深为1.5~2 m,堵塞长度为3.5~4 m,孔、排距分别为4.5 m、4 m,台阶高度为10~13 m。利用Blast-UM 爆破测振仪,在矿山西帮台阶布置相应的拾振点采集质点振动速度,如图7 所示。爆破振动监测结果见表2。
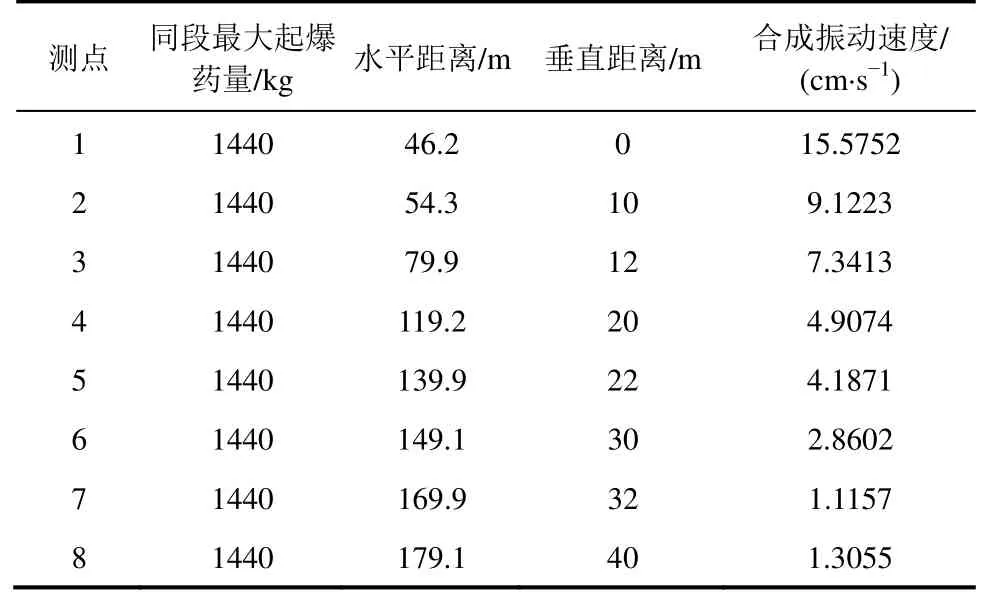
表2 爆破振动监测结果
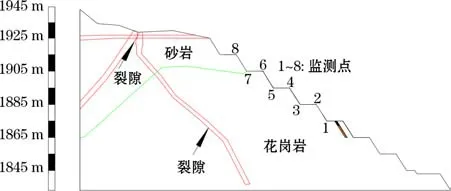
图7 测点布置台阶剖面
表格中同一平台中垂直距离不一致,这是由于现场平台不够平整以及拾振点的布置原因所造成的。结合式(3)~式(5),对上述表格数据进行处理得出:

其相关性系数r2=0.98739;萨道夫斯基公式拟合相关系数为0.9159,其相关性系数大于0.9,且在第3~4 级台阶出现放大效应,其放大系数为1.17倍,这是由于台阶高度之间的区域内部地质条件复杂,即节理裂隙发育、含水量丰富等原因,影响了爆炸应力波的传播。
5 结论
利用ANSYS/LS-DYNA 有限元软件进行数值模型研究,并结合现场爆破实例,分析台阶高度对爆破振动速度的影响,得出以下结论:
(1)通过数值模拟分析台阶地形对临界振速的影响,得到台阶临界振动随距离的增加整体上呈指数衰减,并验证了改进公式的合理性;就单一台阶而言,由于高差的存在,使得坡顶处临界速度放大;然而放大倍数不会随着高度的增加呈正相关,而是当高度超过一定值时,放大倍数呈减小趋势。
(2)分析现场工程爆破振动数据可知,其相关性系数大于0.9,且其在第3~4 级台阶出现放大效应,这是由于台阶高度之间局部地质条件复杂所造成的,并验证了改进公式的合理性。

